Discentreco

Discentreco ĝenerale estas eco de io discentra.

Matematiko

En la matematiko, discentreco ((laŭ PIV) aŭ fokusdiseco (laŭ NPIV) estas la parametro asociita kun ĉiu ajn konika sekco; ĝi estas la konstanta rilato inter la distanco de ĉiu punkto de la koniko al ĝia fokuso (F) kaj la distanco de tiu punkto al la direktanto (D):

• La discentreco de cirklo estas nulo.
• La discentreco de elipso estas pli granda ol nulo sed malpli ol 1
• La discentreco de parabolo estas 1.
• La discentreco de hiperbolo estas pli granda ol 1.
• La discentreco de rekta linio estas malfinio.

Elementoj de elipso, ĉi tie: ${\displaystyle \epsilon ={\frac {f}{a}}=0,8}$

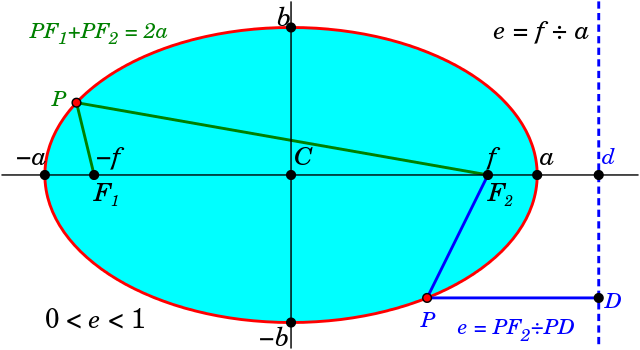
Ĉe iu ajn elipso, kie la longo de la granda duonakso estas a, kaj la malgranda duonakso estas b, la distanco ${\displaystyle f}$ de la du fokusoj (F1 aŭ F2) al la centro (C) estas:

${\displaystyle f={\sqrt {{a^{2}}-{b^{2}}}}}$ .

La discentreco estas:

${\displaystyle \epsilon ={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$

La sendimensia numera discentreco uzas la grekan literon epsilono ${\displaystyle {\boldsymbol {\epsilon }}}$ (por eviti la konfuzon kun ${\displaystyle {\boldsymbol {e}}}$ , kiu simbolas la "linearan discentrecon":

${\displaystyle e=\epsilon {a}=f}$ )

, kiu estas la proporcio de la distanco ${\displaystyle f}$ de la du fokusoj (F1 aŭ F2) al la granda duonakso , a (Vd la bildon):

${\displaystyle \epsilon ={\frac {2e}{2a}}}$ .

Ĉe iu ajn hiperbolo, domita en karteziaj koordinatoj kiel

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$

, kie la longo de la granda duonakso estas a, kaj la longo de malgranda duonakso estas b, la discentreco de la hiperbolo estas:

${\displaystyle \epsilon ={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$

. Tie la distanco ${\displaystyle f}$ de la du fokusoj (F1 aŭ F2) al la centro estas:

${\displaystyle f={\sqrt {{a^{2}}+{b^{2}}}}}$ .

Astronomio

En la astronomio, discentreco de orbito kalkuleblas per la supre menciitaj formuloj, se la formo de la orbito konatas.

Ekzemple, la discentreco de la Tera orbito estas 0,0167.

La discentreco estas kalkulebla ankaŭ per metodoj, kiuj baziĝas sur la orbita energio kaj angula movokvanto.

En astrodinamiko, la orbita discentreco de astronomia objekto estas sendimensia parametro, kiu determinas la kvanton laŭ kiu ĝia orbito ĉirkaŭ alia korpo devias de perfekta cirklo.

• Kategorio Discentreco en la Vikimedia Komunejo (Multrimedaj datumoj)
• Discentreco en ReVo