Leĝo de kosinusoj
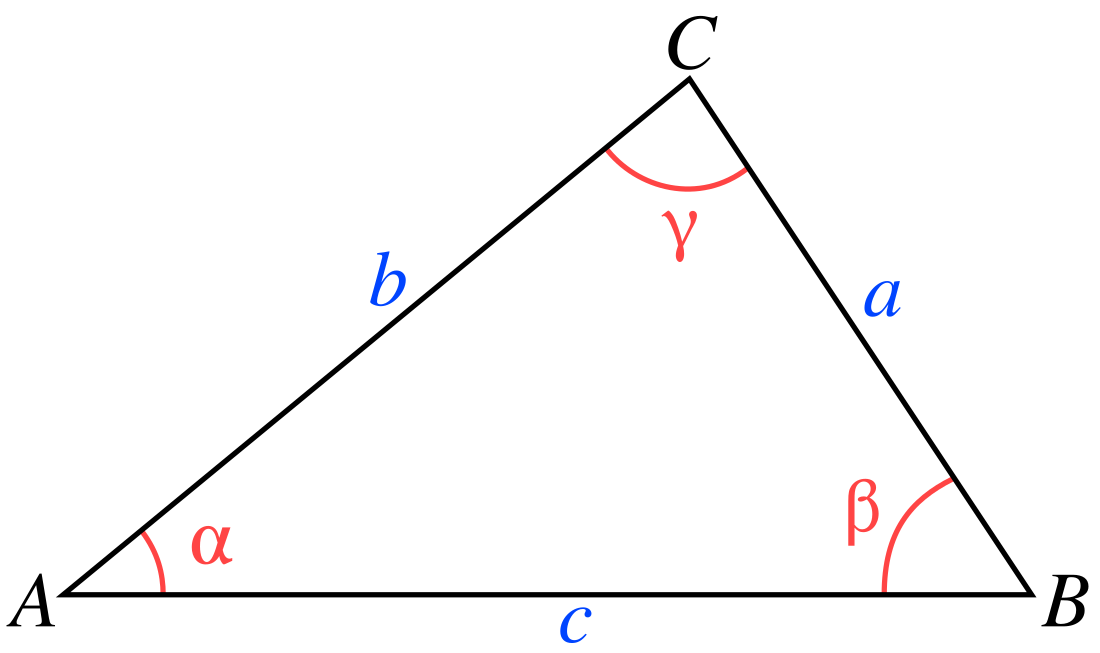
teoremo de Eŭklida geometrio ke, se la longoj de la tri lateroj de triangulo estas a, b, kaj c, do c²=a²+b²−2ab cos(C), je kiu C estas la angulo kontraŭ c From Wikipedia, the free encyclopedia
Remove ads
En trigonometrio, la leĝo de kosinusoj, nomita ankaŭ kosinusa formulo, kosinusa regulo, kosinusa teoremo aŭ kosinusa teoremo de Carnot, estas interrilato inter longoj de lateroj kaj kosinuso de unu el anguloj ĉe triangulo sur eŭklida ebeno.
| Ĉi tiu artikolo temas pri leĝo de kosinusoj en eŭklida geometrio. Por teoremo en sfera geometrio rigardu la paĝon Sfera leĝo de kosinusoj. |

kie c estas longoj de latero kontraŭa al angulo γ,
- a kaj b estas longoj de latero inter kiuj estas angulo γ.
Ekvivalente por la aliaj anguloj de la triangulo la leĝo estas:
La leĝo de kosinusoj estas ĝeneraligo de la teoremo de Pitagoro, kiu veras nur por ortaj trianguloj: se la angulo γ estas orto (90° aŭ π/2 radianoj), tiam cos γ=0, kaj tial la leĝo de kosinusoj reduktiĝas al
kio estas la teoremo de Pitagoro.
Remove ads
Aplikoj

La leĝo de kosinusoj povas esti uzata por komputi la trian lateron de triangulo se du lateroj kaj angulo inter ili estas sciataj:
Tiel la teoremo estas uzata en triangulado.
La leĝo de kosinusoj povas esti uzata por komputanti angulojn de triangulo se ĉiuj tri lateroj estas sciataj:
La leĝo de kosinusoj povas esti uzata por komputi la trian lateron de triangulo se du lateroj kaj angulo kontraŭa al unu el ili estas sciataj:
Ĉi tiuj formuloj produktas grandajn rondigajn erarojn en flosantaj punktaj kalkuloj se la triangulo estas tre akuta, kio estas, se c estas malgranda relative al a kaj b aŭ γ estas malgranda.
La tria formulo estas la rezulto de solvado por a de la kvadrata ekvacio
- a2 − 2ab cos γ + b2 − c2 = 0.
Ĉi tiu ekvacio povas havi 0, 1 aŭ 2 pozitivajn solvaĵojn depende de kvanto de eblaj trianguloj donitaj per la datumoj b, c kaj γ. Estas du pozitivaj solvaĵoj se b sin(γ) < c < b, nur unu pozitiva solvaĵo se c > b aŭ c = b sin(C), kaj ne estas pozitivaj solvaĵoj se c < b sin(γ). Ĉi tiuj malsamaj okazoj estas ankaŭ eksplikitaj per la latero-latero-angula kongrueca multvaloreco.
Remove ads
Pruvo
Konsideri triangulo kun lateroj de longoj a, b, c, kie estas γ la angulo kontraŭa la latero de longo c. Situu ĉi tiu triangulo sur la koordinatsistemo tiel ke la verticoj estu kun koordinatoj A (b cos γ, b sin γ), B(a,0), C(0,0). Per la distanca formulo, kaj plu:
Remove ads
Izocela okazo
Se la triangulo estas izocela, a = b, la leĝo de kosinusoj plisimpliĝas) grave. Ĉar tiam a2 + b2 = 2a2 = 2ab, la leĝo de kosinusoj iĝas kiel
Analogo por kvaredroj
Estu areoj de la kvar edroj de kvaredro. Estu la duedraj anguloj per kaj tiel plu. Tiam
Remove ads
Vidu ankaŭ
Eksteraj ligiloj
- Leĝo de kosinusoj Arkivigite je 2008-04-18 per la retarkivo Wayback Machine je PlainMath
- Kelkaj derivaĵoj de la kosinusa leĝo je tranĉi-la-nodon
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads