Vektoro

Vektoro estas matematika objekto kiu estas difinita per nombro (sia longo, aŭ normo) kaj sia direkto. Oni povas desegni ĝin per sago.

Ĉi tiu artikolo temas pri matematika objekto. Por termino en epidemiologio rigardu la paĝon Vektoro (epidemiologio).

Du vektoroj ${\displaystyle {\overrightarrow {u}}}$ kaj ${\displaystyle {\overrightarrow {v}}}$ kaj ilia vektora sumo.

Pli ĝenerale, en la lineara algebro vektoro estas difinita kiel elemento de vektorspaco. Tiu estas multe pli ampleksa difino, kiu entenas krom la "ordinarajn" geometriajn vektorojn, kaj krom n-dimensiajn vektorojn (n pozitiva entjero), ankaŭ diversajn aliajn matematikajn objektojn (nombrojn, vicojn, funkciojn kaj bildigojn). Laŭ tiu difino ankaŭ ĉiuj tensoroj estas vektoroj.

En la diferenciala geometrio, la fiziko kaj la tekniko la esprimo vektoro plej ofte alcelas la geometrian vektoron de la eŭklida spaco, kiu estas difinta de sia longeco kaj direkto. Ekzemploj estas situa vektoro, vektora rapido, impulso, forto, momanto kaj akcelo. Laŭ ĉi tiu difino vektoro estas unuagrada tensoro.

En matrica algebro, vektoro estas n×1 matrico - kolumna vektoro aŭ 1×n matrico - linia vektoro. Ĉi tiuj vektoroj estas prezentoj de geometria vektoro en iu bazo.

Operacioj per vektoroj

Adiciaj

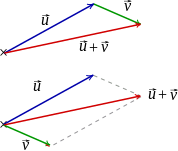
Adicio de vektoro plus vektoro rezultigas vektoron. Subtraho estas sama kiel adicio kun inversa vektoro.

Multiplikaj

Pli detalaj informoj troveblas en artikolo Multipliko de vektoroj.

• Skalara multipliko -- unu vektoro kaj unu skalaro eniras, rezulto estas vektoro
• Skalara produto -- du vektoroj eniras, rezulto estas skalaro
• Vektora produto -- du vektoroj eniras, rezulto estas vektoro

Vidu ankaŭ

• Atraktoro
• Vektora kalkulo
• Vektora spaco

Aliaj projektoj

• Kategorio Vektoro en la Vikimedia Komunejo (Multrimedaj datumoj)
• Vektoro en ReVo

Ĉi tiu artikolo ankoraŭ estas ĝermo pri matematiko. Helpu al Vikipedio plilongigi ĝin. Se jam ekzistas alilingva samtema artikolo pli disvolvita, traduku kaj aldonu el ĝi (menciante la fonton).