Filtro de imagen compuesta

Un filtro de imagen compuesto es un filtro electrónico formado por múltiples secciones de filtro de imagen de dos o más tipos diferentes.

El método de imagen de diseño de filtros determina las propiedades de las secciones de filtro calculando las propiedades que tendrían en una cadena infinita de secciones idénticas. En este sentido, el análisis es paralelo a la teoría de líneas de transmisión en la que se basa. Los filtros diseñados según este método se denominan filtros de parámetros de imagen, o simplemente filtros de imagen. Un parámetro importante de los filtros imagen es su impedancia imagen, la impedancia de una cadena infinita de secciones idénticas.

Las secciones básicas se organizan en una red en escalera de varias secciones; el número de secciones necesarias viene determinado principalmente por la cantidad de rechazo de banda de parada que se requiera. En su forma más sencilla, el filtro puede estar compuesto en su totalidad por secciones idénticas. Sin embargo, lo más habitual es utilizar un filtro compuesto de dos o tres tipos diferentes de secciones para mejorar distintos parámetros que se abordan mejor con un tipo concreto. Los parámetros más frecuentemente considerados son el rechazo de la banda de parada, la inclinación de la falda del filtro (banda de transición) y la adaptación de la impedancia a las terminaciones del filtro.

Los filtros de imagen son filtros lineales e invariablemente también pasivos en su implementación.

Historia

El método de diseño de filtros de imagen se originó en AT&T, que estaba interesada en desarrollar un filtrado que pudiera utilizarse con la multiplexación de muchos canales telefónicos en un solo cable. A continuación se enumeran brevemente los investigadores que participaron en este trabajo y sus contribuciones;

• John Carson aportó los fundamentos matemáticos de la teoría. Inventó la modulación de banda lateral única para multiplexar canales telefónicos. La necesidad de recuperar estas señales dio lugar a la necesidad de técnicas avanzadas de filtrado. También fue pionero en el uso del cálculo operacional (lo que ahora se ha convertido en la teoría de las transformadas de Laplace en su forma matemática más formal) para analizar estas señales.^[1]
• George Campbell trabajó en el filtrado a partir de 1910 e inventó el filtro de k constante,^[2] que puede considerarse una continuación de su trabajo sobre las bobinas de carga en las líneas de transmisión, un concepto inventado por Oliver Heaviside. Heaviside, por cierto, también inventó el cálculo operacional que utilizaba Carson.^[3]
• Otto Zobel proporcionó una base teórica (y el nombre) para los filtros de Campbell. En 1920 inventó el filtro derivado de m. Zobel también publicó diseños compuestos que incorporaban tanto k constante como secciones derivadas de m.^[4]
• R. S. Hoyt también contribuyó.^[5][6]

El método de la imagen

El análisis de imagen comienza con un cálculo de las impedancias de entrada y salida (las impedancias de imagen) y la función de transferencia de una sección en una cadena infinita de secciones idénticas. Por tanto, el método de la imagen se basa en que cada sección del filtro esté terminada con la impedancia de imagen correcta.^[7] Esto es bastante fácil de hacer con las secciones internas de un filtro de secciones múltiples, ya que sólo es necesario asegurarse de que las secciones orientadas hacia el filtro en cuestión tengan impedancias de imagen idénticas. Sin embargo, las secciones finales son un problema. Normalmente estarán terminadas con resistencias fijas que el filtro no puede hacer coincidir perfectamente excepto en una frecuencia específica. Este desajuste provoca múltiples reflexiones en las terminaciones del filtro y en las uniones entre secciones. Estas reflexiones hacen que la respuesta del filtro se desvíe bastante de la teórica, especialmente cerca de la frecuencia de corte.^[8]

El requisito de una mejor adaptación a las impedancias finales es una de las principales motivaciones para utilizar filtros compuestos. En los extremos se utiliza una sección diseñada para proporcionar una buena adaptación, pero para el cuerpo del filtro se diseña algo distinto (por ejemplo, rechazo de banda de parada o transición de banda de paso a banda de parada).

Tipos de secciones de filtro

Cada tipo de sección de filtro tiene sus ventajas e inconvenientes, y cada una de ellas puede mejorar determinados parámetros del filtro. Las secciones que se describen a continuación son los prototipos de filtros para secciones paso-bajo. Estos prototipos pueden escalarse y transformarse a la forma de banda de frecuencia deseada (pasa-bajas, pasa-altas, pasa-banda o pasa-banda).

La unidad más pequeña de un filtro de imagen es una semisección L. Como la sección L no es simétrica, tiene diferentes impedancias de imagen (𝑍𝑖) en cada lado. Estas impedancias se denominan 𝑍𝑖𝑇 y 𝑍𝑖𝛱.

La T y la Π del sufijo se refieren a la forma de la sección del filtro que se formaría si se conectaran dos medias secciones espalda con espalda. T y Π son las secciones simétricas más pequeñas que se pueden construir, como se muestra en los diagramas de la tabla topológica (abajo). Cuando la sección en cuestión tiene una impedancia de imagen diferente del caso general, se añade un sufijo adicional que identifica el tipo de sección, por ejemplo 𝑍𝑖𝑇𝑚.

Sección k constante

La sección de filtro k constante o de tipo k es la sección de filtro de imagen básica. También es la topología de circuito más sencilla. El tipo k tiene una transición moderadamente rápida de la banda pasante a la banda de parada y un rechazo moderadamente bueno de la banda de parada.

• 
  filtro paso bajo de media sección tipo k
• 
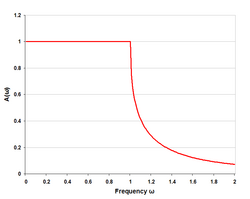
  respuesta pasa bajo tipo k con cuatro (medias) secciones

Sección m-derivada

La sección de filtro derivada de m o de tipo m es una evolución de la sección de tipo k. La característica más destacada del tipo m es un polo de atenuación justo después de la frecuencia de corte dentro de la banda de parada. El parámetro m ( 0 < m < 1 ) ajusta la posición de este polo de atenuación. Los valores más pequeños de m acercan el polo a la frecuencia de corte. Valores mayores de m lo alejan. En el límite, a medida que m se aproxima a 1, el polo se aproxima a ω de infinito y la sección se aproxima a una sección de tipo k.

El tipo m tiene un corte especialmente rápido, que va de totalmente pasante a la frecuencia de corte a totalmente pasante a la frecuencia del polo. El corte puede hacerse más rápido acercando el polo a la frecuencia de corte. Este filtro tiene el corte más rápido de todos los diseños de filtro; tenga en cuenta que la transición rápida se consigue con una sola sección, no hay necesidad de múltiples secciones. El inconveniente de las secciones de tipo m es que tienen un pobre rechazo de la banda de parada pasado el polo de atenuación.

Hay una propiedad especialmente útil de los filtros de tipo m con m=0,6 . Estos tienen una impedancia de imagen plana máxima

𝑍𝑖𝑚en la banda pasante. Por lo tanto, son adecuados para adaptarse a las terminaciones del filtro, al menos en la banda pasante; la banda de parada es otra historia.

Hay dos variantes de la sección de tipo m, en serie y en derivación. Tienen funciones de transferencia idénticas, pero sus impedancias de imagen son diferentes. La sección en derivación tiene una impedancia imagen que coincide con 𝑍𝑖𝛱 por un lado, pero tiene una impedancia diferente, 𝑍𝑖𝑇𝑚en el otro. La semisección en serie coincide con 𝑍𝑖𝑇 por un lado y tiene 𝑍𝑖𝛱𝑚 en el otro.

• 
  filtro paso bajo tipo m de media sección en derivación
• 
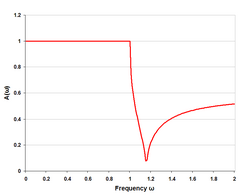
  respuesta pasa bajo tipo m de media sección simple m=0,5
• 
  respuesta pasa bajo tipo m con cuatro (medias) secciones m=0,5
• 
  filtro paso bajo tipo m de media sección en serie
• 
  respuesta pasa bajo tipo m de media sección simple m=0,75
• 
  respuesta pasa bajo tipo m de media sección simple m=0,25

Sección tipo mm′

La sección de tipo mm′ tiene dos parámetros independientes (m y m′) que el diseñador puede ajustar. Se obtiene mediante la doble aplicación del proceso de derivación m. Su principal ventaja es que se adapta mejor a las terminaciones resistivas que el tipo k o el tipo m. La impedancia imagen de una media sección es 𝑍𝑖𝑚en un lado y una impedancia diferente 𝑍𝑖𝑚𝑚′en el otro. Al igual que el tipo m, esta sección puede construirse en serie o en derivación y las impedancias de imagen vendrán en variantes T y Π. Se aplica una construcción en serie a un tipo m en derivación o una construcción en derivación a un tipo m en serie. Las ventajas del filtro de tipo mm′ se consiguen a expensas de una mayor complejidad del circuito, por lo que normalmente sólo se utilizaría cuando fuera necesario a efectos de adaptación de impedancias y no en el cuerpo del filtro.

La función de transferencia de un tipo mm′ es la misma que la de un tipo m con mm′ ajustado al producto mm′. Para elegir los valores de m y m′ para la mejor adaptación de impedancia, el diseñador debe elegir dos frecuencias en las que la adaptación debe ser exacta; en otras frecuencias habrá alguna desviación. Por lo tanto, hay cierto margen en la elección, pero Zobel sugiere^[9] los valores m=0,7230 y m′=0,4134, que dan una desviación de la impedancia inferior al 2% en la parte útil de la banda. Dado que mm′=0,3, esta sección también tendrá un corte mucho más rápido que un tipo m de m=0,6 que es una alternativa para la adaptación de impedancias.

Es posible continuar el proceso de m-derivación repetidamente y producir m′m″-tipos y así sucesivamente. Sin embargo, las mejoras obtenidas disminuyen en cada iteración y no suele merecer la pena el aumento de complejidad.

• 
  filtro paso bajo tipo mm′ de media sección en serie
• 
  respuesta pasa bajo tipo m de media sección simple m=0,6
• 
  respuesta pasa bajo tipo mm′ de media sección simple mm′=0,3

Filtro de Bode

Una encarnación del filtro de Bode como filtro de paso bajo

Hendrik Bode describió otra variación del filtro de tipo m. Este filtro utiliza como prototipo un filtro derivado de m de serie media y lo transforma en una topología en T puenteada con la adición de una resistencia puenteadora. Esta sección tiene la ventaja de poder situar el polo de atenuación mucho más cerca de la frecuencia de corte que el filtro Zobel, que empieza a no funcionar correctamente con valores muy pequeños de m debido a la resistencia del inductor. Ver transformadas de impedancia equivalentes para una explicación de su funcionamiento.^[10]

Red de Zobel

La característica distintiva de los filtros de red de Zobel es que tienen una impedancia de imagen de resistencia constante y por esta razón también se conocen como redes de resistencia constante. Evidentemente, el filtro de red Zobel no tiene problemas de adaptación a sus terminaciones y ésta es su principal ventaja. Sin embargo, otros tipos de filtros tienen funciones de transferencia más pronunciadas y cortes más agudos. En las aplicaciones de filtrado, el papel principal de las redes de Zobel es como filtros de ecualización. Las redes de Zobel pertenecen a un grupo diferente del de otros filtros de imagen. La resistencia constante hace que cuando se utilizan en combinación con otras secciones de filtros de imagen surja el mismo problema de igualación que con las terminaciones. Las redes de Zobel también sufren la desventaja de utilizar muchos más componentes que otras secciones de imagen equivalentes.

• 
  Puente de red Zobel Sección de filtro paso alto T
• 
  Red Zobel de respuesta pasa bajo de sección única
• 
  Red de Zobel respuesta pasa bajo cinco secciones

Efecto de las terminaciones

Una consecuencia del método de imagen para el diseño de filtros es que el efecto de las terminaciones finales debe calcularse por separado si se quieren tener en cuenta sus efectos sobre la respuesta. La mayor desviación de la respuesta respecto a la prevista se produce en la banda de paso próxima al corte. La razón es doble. En la banda de paso, la impedancia mejora progresivamente, lo que limita el error. Por otro lado, las ondas de la banda de paso se reflejan en la terminación final debido a la desadaptación, pero el rechazo de la banda de paso del filtro las atenúa dos veces al atravesarla. Por tanto, aunque el desajuste de impedancia de la banda de parada puede ser grave, sólo tiene un efecto limitado en la respuesta del filtro.

• 
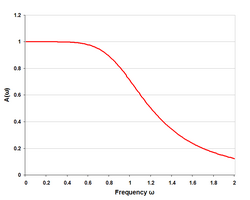
  Respuesta teórica del filtro en T de paso bajo tipo k (dos semisecciones) cuando está correctamente terminado en impedancia de imagen
• 
  Respuesta práctica del filtro en T de paso bajo tipo k (dos semisecciones) cuando se termina con resistencias fijas

Secciones en cascada

Varias semisecciones L pueden conectarse en cascada para formar un filtro compuesto. La regla más importante a la hora de construir un filtro de imagen compuesto es que las impedancias de imagen siempre deben enfrentarse a una impedancia idéntica; lo semejante siempre debe enfrentarse a lo semejante. Las secciones T siempre deben enfrentarse a las secciones T, las secciones Π siempre deben enfrentarse a las secciones Π, el tipo k siempre debe enfrentarse al tipo k (o al lado de un tipo m que tenga la impedancia del tipo k) y el tipo m siempre debe enfrentarse al tipo m. Además, las impedancias de tipo m de diferentes valores de m no pueden enfrentarse entre sí. Tampoco pueden hacerlo las secciones de cualquier tipo que tengan diferentes valores de frecuencia de corte.

Las secciones al principio y al final del filtro se eligen a menudo por su adaptación de impedancia a las terminaciones más que por la forma de su respuesta en frecuencia. Para este fin, las secciones de tipo m de m = 0,6 son la elección más común.^[11]Una alternativa son las secciones de tipo mm′ de m=0,7230 y m′=0,4134, aunque este tipo de sección se utiliza raramente. Aunque tiene varias ventajas que se señalan a continuación, presenta el inconveniente de ser más compleja y, además, si se requieren secciones k constantes en el cuerpo del filtro, entonces es necesario incluir secciones de tipo m para interconectar las de tipo mm′ con las de tipo k.^[12]

Las secciones interiores del filtro suelen ser de k constante, ya que son las que producen la mayor atenuación en la banda de parada. Sin embargo, también pueden incluirse una o dos secciones de tipo m para mejorar la velocidad de caída de la banda de paso a la de parada. Se elige un valor bajo de m para los tipos m utilizados con este fin. Cuanto menor sea el valor de m, más rápida será la transición, mientras que, al mismo tiempo, la atenuación de la banda de parada será menor, lo que aumentará la necesidad de utilizar también secciones adicionales de tipo k. Una ventaja de utilizar secciones de tipo mm′ para la adaptación de impedancias es que este tipo de secciones finales tendrán una transición rápida de todos modos (mucho más que las de tipo m=0,6) porque mm′=0,3 para la adaptación de impedancias. Así que la necesidad de secciones en el cuerpo del filtro para hacer esto se puede prescindir.

Ejemplo típico de un filtro de imagen compuesto en forma de diagrama de bloques. Se muestran las impedancias de imagen y cómo coinciden.

El filtro anterior se realiza como un filtro de paso bajo en escalera. Los valores de los componentes se dan en términos de L y C, los valores de los componentes de una semisección k constante.

El mismo filtro minimizado mediante la combinación de componentes en serie o en paralelo en su caso.

Otra razón para utilizar tipos m en el cuerpo del filtro es colocar un polo adicional de atenuación en la banda de parada. La frecuencia del polo depende directamente del valor de m. Cuanto menor sea el valor de m, más cerca estará el polo de la frecuencia de corte. A la inversa, un valor grande de m aleja el polo de la frecuencia de corte hasta que en el límite cuando m=1 el polo está en el infinito y la respuesta es la misma que la de la sección de tipo k. Si se elige un valor de m para este polo que sea diferente del polo de las secciones extremas, tendrá el efecto de ampliar la banda de buen rechazo de la banda de parada cerca de la frecuencia de corte. De este modo, las secciones de tipo m sirven para proporcionar un buen rechazo de la banda de parada cerca de la frecuencia de corte y las secciones de tipo k proporcionan un buen rechazo de la banda de parada lejos de la frecuencia de corte. Alternativamente, se pueden utilizar secciones de tipo m en el cuerpo del filtro con diferentes valores de m si el valor encontrado en las secciones finales no es adecuado. También en este caso, el tipo mm′ tendría algunas ventajas si se utilizara para la adaptación de impedancias. El tipo mm′ utilizado para la adaptación de impedancias sitúa el polo en m=0,3 . Sin embargo, la otra mitad de la sección de adaptación de la impedancia debe ser de tipo m de m=0,723.^[9]Esto proporciona automáticamente una buena dispersión del rechazo de la banda de parada y, al igual que con el problema de la inclinación de la transición, el uso de secciones de tipo mm′ puede eliminar la necesidad de secciones de tipo m adicionales en el cuerpo.

Las secciones de resistencia constante también pueden ser necesarias, si el filtro se utiliza en una línea de transmisión, para mejorar la planitud de la respuesta de la banda de paso. Esto es necesario porque la respuesta de la línea de transmisión no suele ser perfectamente plana. Estas secciones se colocan normalmente más cerca de la línea, ya que presentan una impedancia predecible para la línea y también tienden a enmascarar la impedancia indeterminada de la línea del resto del filtro. No hay ningún problema con la adaptación de las secciones de resistencia constante entre sí, incluso cuando las secciones están operando en bandas de frecuencia totalmente diferentes. Se puede hacer que todas las secciones tengan exactamente la misma impedancia imagen de una resistencia fija.

Véase también

Tipos de filtros de imagen

• Filtro m-derivado
• Red Zobel

Conceptos de diseño

• Bobina de Pupin

Personas

• Oliver Heaviside
• Otto Zobel