Runcinado

En geometría, el runcinado es una operación que consiste en cortar un politopo regular (o un panal multicelda) simultáneamente en las caras, aristas y vértices, creando nuevas facetas en lugar de los centros originales de caras, aristas y vértices.^[1]

Un panal de abeja cúbico runcinado (parcial) - Las celdas originales (cubos morados) se reducen en tamaño. Las caras se convierten en nuevas celdas cúbicas azules. Los bordes se convierten en nuevas celdas cúbicas rojas. Los vértices se convierten en nuevas celdas cúbicas (ocultas).

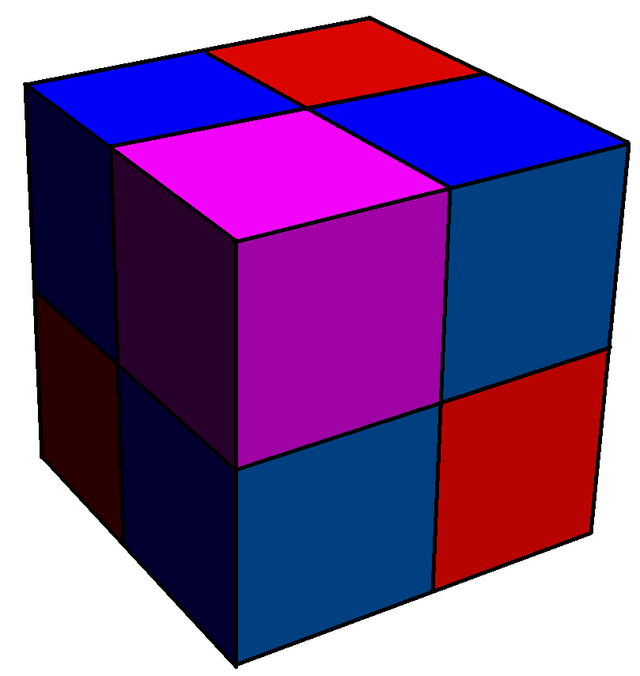
Es una operación de truncamiento generalizada a politopos de dimensiones superiores al espacio euclídeo,^[2] y sigue al canteado y al truncado.

Propiedades

Está representado por un Símbolo de Schläfli t_0,3{p,q,...} extendido. Esta operación solo existe para polícoros {p, q, r} o superiores.

Esta operación es simétrica dual para los 4-politopos regulares y panales uniformes convexos tridimensionales.

Para un 4-politopo {p,q,r} regular, las celdas originales {p,q} permanecen, pero se separan. Los huecos en las caras separadas se convierten en prismas p-gonales. Los espacios entre los bordes separados se convierten en prismas r-gonales. Los espacios entre los vértices separados se convierten en celdas {r, q}. La figura de vértice para un politopo regular de 4 {p,q,r} es un antiprisma q-gonal (llamado antípodio si p y r son diferentes).

Para 4-politopos/panales regulares, esta operación también se llama expansión en la terminología empleada por Alicia Boole Stott, y se puede imaginar moviendo las caras de la forma regular lejos del centro y generando caras nuevas en los huecos para cada vértice abierto y aristas que han quedado al descubierto.

Formas de 4-politopos/panales runcinados:

Símbolo de Schläfli Diagrama de Coxeter-Dynkin	Nombre	Figura de vértice	Imagen
4-politopos uniformes
t0,3{3,3,3}	5-celdas runcinado
t0,3{3,3,4}	16-celdas runcinado (Lo mismo que el 8-celdas runcinado)
t0,3{3,4,3}	24-celdas runcinado
t0,3{3,3,5}	120-celdas runcinado (Lo mismo que el 600-celdas runcinado)
Panales uniformes convexos euclídeos
t0,3{4,3,4}	Panal cúbico runcinado (Lo mismo que el panal cúbico)
Panales uniformes hiperbólicos
t0,3{4,3,5}	Panal cúbico de orden 5 runcinado
t0,3{3,5,3}	Panal icosaédrico runcinado
t0,3{5,3,5}	Panal dodecaédrico de orden 5 runcinado

Véase también

• Poliedro uniforme
• 4-politopo uniforme
• Rectificación (geometría)
• Truncamiento (geometría)
• Canteado (geometría)