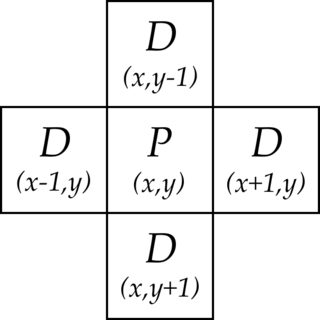Top Qs
Línea de tiempo
Chat
Contexto
Vecindad de von Neumann
De Wikipedia, la enciclopedia libre
Remove ads
En la teoría de autómatas celulares, el concepto de vecindad de von Neumann se define como el conjunto de las cuatro celdas que rodean ortogonalmente a una celda central en un enrejado cuadrado bidimensional.[1] Debe su nombre a John von Neumann, quien utilizó este concepto para definir en su interior el autómata celular de von Neumann y el constructor universal de von Neumann.[2] Es uno de los dos criterios de vecindad más utilizados generalmente para autómatas celulares bidimensionales. El otro es el de vecindad de Moore. Es similar a la idea de la conexión de 4 píxeles en los gráficos de ordenador.[3]
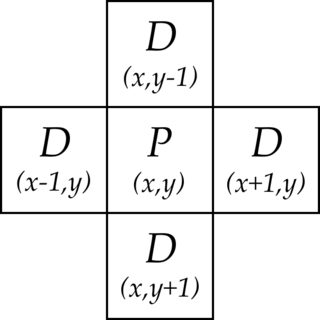

El concepto puede ser extendido a dimensiones más altas, por ejemplo formando una vecindad octaédrica de 6 celdas para un autómata celular cúbico en tres dimensiones.[4]
La vecindad de von Neumann de un punto es el conjunto de puntos situados a una distancia de Manhattan de valor 1 respecto al punto dado.
Remove ads
Vecindad de von Neumann de rango r
La extensión del concepto de la vecindad de von Neumann sencilla descrita anteriormente, también sirve para determinar el conjunto de puntos a una distancia de Manhattan con r > 1. El resultado es una región en forma de diamante (se muestra para r = 2 en la ilustración). Se denominan vencindades de von Neumann de rango o extensión r. El número de celdas de la vecindad de von Neumann para un espacio d-dimensional y rango r es el correspondiente número de Delannoy D(d,r).[4]
Remove ads
Véase también
Referencias
Enlaces externos
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads