Sirge

Sirge ehk sirgjoon on ilma läbimõõduta, mõlemas suunas lõpmata pikk, kõverusteta joon ehk ühemõõtmeline ruum, mis võib sisalduda mitmemõõtmelises ruumis.^[1]

Sirge tasandil

Üldvõrrand

Sirge üldvõrrand tasandil on (Descartesi koordinaadistikus) ristkoordinaadistikus lineaarvõrrand ${\displaystyle Ax+By+C=0}$, kus ${\displaystyle A}$, ${\displaystyle B}$ ja ${\displaystyle C}$ on konstandid, kusjuures ${\displaystyle A}$ ja ${\displaystyle B}$ ei võrdu samaaegselt nulliga.

Näide

Sirge võrrand tasandil:

${\displaystyle 4x-1y-1=0{\text{ ehk }}y=4x-1}$

Parameetriline kuju

Kasutatakse üldvõrrandi ${\displaystyle Ax+By+C=0}$ parameetrilist kuju ${\displaystyle L=\left\{{\begin{array}{c}x=x_{0}+ta\\y=y_{0}+tb\end{array}}\right.{\text{, kus }}t\in \mathbb {R} }$^[2][3]

Näide

${\displaystyle \mathbb {R} ^{2}}$, kus sirge on määratud 2 vektori kaudu ${\displaystyle \alpha =\left({\begin{array}{c}2\\4\end{array}}\right){\text{ ja }}\beta =\left({\begin{array}{c}3\\3\end{array}}\right)}$ :

${\displaystyle L={a+t({\overrightarrow {\beta -\alpha }}),{\text{ kus }}t\in \mathbb {R} }={\left({\begin{array}{c}2+t\\4-t\end{array}}\right),{\text{ kus }}t\in \mathbb {R} }}$

või

${\displaystyle L={b+t({\overrightarrow {\beta -\alpha }}),{\text{ kus }}t\in \mathbb {R} }={\left({\begin{array}{c}3+t\\3-t\end{array}}\right),{\text{ kus }}t\in \mathbb {R} }}$

Lisaks eelnimetatule on võimalik parameetrilist kuju tähistada, kui parameetrilisi võrrandeid

${\displaystyle L=\left\{{\begin{array}{c}x_{1}=a_{1}+ts_{1}\\x_{2}=a_{2}+ts_{2}\end{array}}\right.{\text{, kus }}t\in \mathbb {R} =\left\{{\begin{array}{c}x_{1}=3+t\\x_{2}=3-t\end{array}}\right.{\text{, kus }}t\in \mathbb {R} }$

ja (Descartesi kujul) ehk kanoonilisel kujul

${\displaystyle {\frac {x_{1}-a_{1}}{s_{1}}}={\frac {x_{2}-a_{2}}{s_{2}}}\to {\frac {x_{1}-2}{1}}={\frac {x_{2}-4}{-1}}\to x_{1}=-x_{2}+6}$

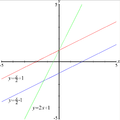
Joonised

• 
  Võrrandiga ${\displaystyle y=4x-1}$ määratud sirge.
• 
  Parameetrilise võrranditega ${\displaystyle x_{1}=3+t}$, ${\displaystyle .x_{2}=3-t}$ määratud sirge.
• 
  Sirged tasandil.

Omadused

Olgu antud sirged ${\displaystyle u}$ ja ${\displaystyle v}$, ning nendele vastavad sihivektorid ${\displaystyle {\vec {s}}_{1}}$ ja ${\displaystyle {\vec {s}}_{2}}$.

Ristuvad sirged

Sirged on risti parajasti siis, kui nende sihivektorite tadamskalaarkorrutis on ${\displaystyle 0}$:

${\displaystyle {\vec {s}}_{1}\cdot {\vec {s}}_{2}=0}$

Paralleelsed sirged

Sirged on paralleelsed parajasti siis, kui nende sihivektorite skalaarkorrutise moodul on ${\displaystyle 1}$:

${\displaystyle |{\vec {s}}_{1}\cdot {\vec {s}}_{2}|=1}$

Kahte punkti saab läbida vaid üks sirge

Eukleidese geomeetrias läbib kahte eri punkti parajasti üks sirge.

Määratud

tõusu ja algordinaadiga

Tõusu (k) ja algordinaadiga (a) määratud sirge võrrand tasandil:

${\displaystyle y=kx+a}$.

kahe punktiga

Kahe punktiga määratud sirge võrrand tasandil:

${\displaystyle {\frac {y-y_{1}}{y_{2}-y_{1}}}={\frac {x-x_{1}}{x_{2}-x_{1}}}}$.

punkti ja sihivektoriga

Punkti ja sihivektoriga määratud sirge võrrand tasandil:

${\displaystyle {\frac {y-y_{1}}{s_{y}}}={\frac {x-x_{1}}{s_{x}}}}$.

punkti ja tõusuga

Punkti ja tõusuga määratud sirge võrrand tasandil:

${\displaystyle y-y_{1}=k(x-x_{1})}$.

kahe tasandi lõikena

Kahe tasandi ${\displaystyle \Pi _{1}:\mathbf {n} _{1}\cdot \mathbf {r} =h_{1}}$ ja ${\displaystyle \Pi _{2}:\mathbf {n} _{2}\cdot \mathbf {r} =h_{2}}$ lõike sirge, kus ${\displaystyle \mathbf {n} _{i}}$ on normaal vektor, on antud

${\displaystyle \mathbf {r} =(c_{1}\mathbf {n} _{1}+c_{2}\mathbf {n} _{2})+\lambda (\mathbf {n} _{1}\times \mathbf {n} _{2})}$

kus

${\displaystyle c_{1}={\frac {h_{1}-h_{2}(\mathbf {n} _{1}\cdot \mathbf {n} _{2})}{1-(\mathbf {n} _{1}\cdot \mathbf {n} _{2})^{2}}}}$

${\displaystyle c_{2}={\frac {h_{2}-h_{1}(\mathbf {n} _{1}\cdot \mathbf {n} _{2})}{1-(\mathbf {n} _{1}\cdot \mathbf {n} _{2})^{2}}}.}$

Rakendatavad funktsioonid

Sirge kaugus punktist ℝ³ ruumis

Olgu antud sirge ${\displaystyle u}$ ja punkt ${\displaystyle D(x_{1};y_{1};z_{1})}$. Olgu sirge ${\displaystyle u}$ sihivektoriks ${\displaystyle {\overrightarrow {s}}=(s_{x};s_{y};s_{z})}$, siis leiame punkti ${\displaystyle X=(x;y;z)}$ sirgel, mis asub sirgel ${\displaystyle u}$ ja mille kaugus on vähim punkti ${\displaystyle D(x_{1};y_{1};z_{1})}$. Selleks lahendame võrrandid:

${\displaystyle {\frac {x-x_{1}}{s_{x}}}={\frac {y-y_{1}}{s_{y}}}={\frac {z-z_{1}}{s_{z}}}}$

Siis leiame vektori ${\displaystyle {\overrightarrow {DX}}}$ ja selle pikkuse ${\displaystyle r=\left|\left|{\overrightarrow {DX}}\right|\right|}$, mis on punkti kaugus sirgest:

${\displaystyle r={\sqrt {\left(x-x_{1}\right){}^{2}+\left(y-y_{1}\right){}^{2}+\left(z-z_{1}\right){}^{2}}}}$

Sirgete kaugus ruumis

Olgu antud sirged ${\displaystyle u}$ ja ${\displaystyle v}$. Sellest leiame vastavad sihivektorid ${\displaystyle {\overrightarrow {s_{1}}}}$ ning ${\displaystyle {\overrightarrow {s_{2}}}}$ ja suvalised punktid mõlemal sirgel vastavalt ${\displaystyle A}$ ja ${\displaystyle B}$.

Paralleelsed sirged

${\displaystyle \varrho ={\frac {\left|\left|{\overrightarrow {s_{1}}}\times {\overrightarrow {\text{AB}}}\right|\right|}{\left|\left|{\overrightarrow {s_{1}}}\right|\right|}}}$

Kiivsirged

${\displaystyle \varrho (u,v)={\frac {\left|({\overrightarrow {s_{1}}}\times {\overrightarrow {s_{2}}})\cdot {\overrightarrow {\text{AB}}}\right|}{\left|\left|{\overrightarrow {s_{1}}}\times {\overrightarrow {s_{2}}}\right|\right|}}}$

Puutuja

${\displaystyle y-y_{1}={\frac {}{}}(f'(x))(x-x_{1})}$

Normaal

${\displaystyle y-y_{1}=\left({\frac {-1}{f'(x)}}\right)(x-x_{1})}$

Vaata ka

• Tuletis
• Punkt
• Sirgete lõikumine
• Kiir
• Lõik