Top Qs
Chronologie
Chat
Contexte
Harmonique (musique)
composante d’un son périodique, dont la fréquence est un multiple entier d'une fréquence fondamentale De Wikipédia, l'encyclopédie libre
Remove ads
En acoustique musicale, un partiel harmonique (ou, plus simplement, un harmonique) est une composante d’un son périodique, dont la fréquence est un multiple entier d'une fréquence fondamentale[1].
Si on appelle « ƒ » la fréquence fondamentale, les partiels harmoniques ont des fréquences égales à : ƒ, 2ƒ, 3ƒ, 4ƒ, 5ƒ, etc.
Exemple :
En prenant comme note fondamentale la3 du piano (440 Hz), les harmoniques ont des fréquences multiples de 440 :
- l'harmonique de rang 1 est la fondamentale, à 440 Hz,
- l'harmonique de rang 2 est à 440 × 2 = 880 Hz,
- celle de rang 3 à 440 × 3 = 1 320 Hz, etc.

Dans une conception traditionnelle du « son musical », les partiels du son musical sont approximativement harmoniques ; les sons franchement non harmoniques y sont parfois décrits comme des « bruits »[2], bien que les percussions, qui n'ont rien d'harmonique, aient toujours fait partie de la musique. Dans les musiques d'aujourd'hui, tout son peut être considéré comme musical dans un contexte approprié[3]. La fondamentale d'un son périodique détermine la hauteur perçue, la puissance relative des partiels harmoniques de rangs supérieurs influe, avec des caractères dynamiques, sur le timbre.
En musique on appelle « harmoniques » les sons qu'on obtient, sur les instruments à cordes, en forçant la vibration d'une corde à un mode supérieur à son mode fondamental. Par exemple, en effleurant la corde au tiers de sa longueur, on empêche son déplacement latéral à cet endroit, tout en la laissant osciller autour de ce point fixe, créant un nœud qui l'oblige à vibrer à une fréquence triple de celle qu'elle aurait libre (avec les harmoniques de cette fréquence). Le son ainsi produit se trouve à un intervalle de douzième — une octave plus une quinte — avec celui de la corde libre.
L'adjectif « harmonique » désigne aussi des caractères qui appartiennent à l'harmonie, qui se rapportent à des sons produits simultanément, par opposition à ceux de la mélodie, émis successivement. L'expression « intervalle harmonique » désigne ainsi un intervalle entre deux sons émis simultanément.
Remove ads
Timbre
Résumé
Contexte

À hauteur (fréquence fondamentale identique), les sons émis par deux instruments différents (par exemple un violon et une flûte) ne sonnent pas de la même manière. Chacun se caractérise par ce qu’on appelle son timbre, qui permet de l’identifier[4]. Cela traduit le fait qu’aucun son réel n’est simple : il résulte de la combinaison de sons partiels. La fréquence d'ensemble de ceux-ci détermine la note de musique que l'on perçoit (voir Fondamentale absente) et leur évolution au cours de l'émission de la note déterminent son timbre.
Les sons produits par les instruments à vibration entretenue, dont la vibration est soutenue par un apport constant d'énergie, par exemple par le frottement de l'archet pour les instruments à cordes, ou par un souffle constant pour l'orgue ou les autres instruments à vent, contiennent de nombreux harmoniques, alors que d'autres instruments comme les percussions émettent des fréquences inharmoniques (2,576ƒ, 5,404ƒ... par exemple pour un triangle). De plus, chaque harmonique possède une intensité relative par rapport aux autres. Le spectre harmonique révèle ainsi l’ensemble des fréquences qui déterminent le timbre de chaque instrument.
Remove ads
Les harmoniques
Résumé
Contexte
La fréquence fondamentale est celle du premier partiel harmonique du son considéré, que l’on désigne comme harmonique 1 ou harmonique fondamental. La note que l’on perçoit correspond à cet harmonique, même s'il est absent du spectre sonore[5]. Certains sons peuvent cependant tromper l’oreille, un harmonique aigu pouvant s’entendre plus que la fondamentale et la cacher[réf. souhaitée].
Les harmoniques d’une note, forcément plus aigus que cette note, sont souvent appelés harmoniques supérieurs[6] par opposition à la théorie des harmoniques inférieurs avancée par certains théoriciens de la musique, et systématisée dans le dualisme harmonique développé par Hauptmann, Oettingen (de) et Riemann.
Le tableau des fréquences de notes ci-dessous indique une correspondance entre les fréquences harmoniques d’une note et les notes qui s’accordent en consonance avec la fondamentale. Ainsi par exemple pour la note do, les notes constituant des intervalles consonants avec elle sont mi (la tierce), sol (la quinte), si ![]() (la septième), do (l’octave), ré (la neuvième), etc. La raison en est qu'un nombre élevé des harmoniques supérieurs de ces notes consonantes sont aussi des harmoniques de la fondamentale : la consonance se définit alors par la concordance entre les harmoniques.
(la septième), do (l’octave), ré (la neuvième), etc. La raison en est qu'un nombre élevé des harmoniques supérieurs de ces notes consonantes sont aussi des harmoniques de la fondamentale : la consonance se définit alors par la concordance entre les harmoniques.
Les harmoniques d’une note sont donnés par les fréquences multiples de la fondamentale. Ainsi pour do à 32,7 Hz noté do−1, les harmoniques sont :
N.B. : les 7e et 11e harmoniques n'ont été utilisés dans l'histoire récente de la musique occidentale que dans les musiques microtonales ou les musiques spectrales.
L’image ci-dessous indique les harmoniques de do1 sur une portée et précise par les flèches et les chiffres (en cents) l’écart de hauteur entre chacun des 16 premiers harmoniques et la note la plus proche dans la gamme tempérée. Considérant que le demi-ton (du tempérament égal) fait 100 cents, la déviation de 31 cents de l'harmonique 7 (écrite la ![]() dans l'exemple ci-dessous) la situe environ un tiers de demi ton plus bas que la septième mineure tempérée (si
dans l'exemple ci-dessous) la situe environ un tiers de demi ton plus bas que la septième mineure tempérée (si ![]() ) et la déviation de 49 cents de l'harmonique 11 est quasiment à mi-chemin entre deux notes existantes (fa et fa
) et la déviation de 49 cents de l'harmonique 11 est quasiment à mi-chemin entre deux notes existantes (fa et fa ![]() ), c’est-à-dire un quart de ton : c'est la raison pourquoi elles ont eu peu d'usage dans la musique classique.
), c’est-à-dire un quart de ton : c'est la raison pourquoi elles ont eu peu d'usage dans la musique classique.

Les écarts des harmoniques avec les notes de la gamme tempérée se retrouvent quelle que soit la note fondamentale et sont propres au rang de l'harmonique.


Remove ads
Applications instrumentales
- Sur un piano, enfoncer doucement la pédale et faire résonner une note, permet de les écouter lorsque l’intensité sonore diminue : les cordes correspondant aux harmoniques vibrent par sympathie ; la série indiquée ci-dessus est alors relativement audible.
- C’est le bon ajustement des harmoniques de deux notes entendues simultanément qui validera la consonance de l’intervalle ou de l’accord entendu. On retrouve bien les raisons pour lesquelles un accord est parfait (do-mi-sol = 4-5-6) : les harmoniques des notes de l’accord sont en concordance avec les harmoniques de la fondamentale.
- Sur les instruments à cordes, on peut faire entendre un son harmonique en effleurant d’un doigt une division entière de la corde. Ci-contre, les divisions correspondant à la fondamentale F (corde à vide) et aux trois premiers harmoniques, et la façon de noter une note ainsi jouée.
Série harmonique
Résumé
Contexte

La série harmonique est l'ensemble des partiels harmoniques[7].
Les instruments de musique à hauteur déterminée (par opposition aux instruments à hauteur indéterminée) sont souvent basés sur un résonateur acoustique tel qu'une corde ou une colonne d'air, qui oscille dans de nombreux modes propres simultanément[8]. Aux fréquences de chaque mode de vibration, des ondes se propagent dans les deux sens le long de la corde ou de la colonne d'air, se renforçant et s'annulant mutuellement pour former des ondes stationnaires. L'interaction avec l'air environnant provoque des ondes sonores audibles, qui s'éloignent de l'instrument. En raison de l'espacement typique des résonances, ces fréquences sont généralement limitées à des multiples entiers, ou harmoniques, de la fréquence la plus basse, et ces multiples forment une série harmonique.
La fréquence du son complexe, correspondant à sa fréquence fondamentale, est généralement perçue comme la hauteur musicale de la note. La puissance relative de chaque harmonique influence le timbre musical.
Terminologie
Un « son complexe » (correspondant au son réel d'une note avec le timbre particulier de l'instrument qui la joue) « peut être décrit comme une combinaison de plusieurs ondes périodiques simples (c'est-à-dire des sinusoïdales) ou « partiels », chacun ayant sa propre fréquence, amplitude et phase[9] ».
Un « son simple » ou « pur »[a] est un son correspondant à une vibration sinusoïdale[11], et possédant donc un seul partiel.
Un partiel est n'importe lequel des sons simples qui composent un son complexe, que leur fréquence soit ou non un multiple entier de la fréquence du son complexe[12].
« PARTIELS. - Terme utilisé en acoustique musicale. Définissent des états vibratoires différents caractéristiques d’un instrument. En fait, dans les instruments classiques les partiels sont des suites de séries harmoniques indépendantes, dont les fondamentaux sont voisins des harmoniques de la série la plus basse qui joue vis-à-vis d’eux le rôle apparent d’un fondamental. Les partiels doivent être considérés comme des séries harmoniques d’états différents de l’instrument (ou résonateur). Pour clarifier cette proposition nous dirions que dans un instrument à vent les différents partiels ne correspondent pas nécessairement à la même colonne d’air excitée. Leurs fréquences n’ont alors aucune raison d’être multiples de la fondamentale. On pourrait interpréter ce fait en disant que, l’énergie emmagasinée étant proportionnelle au carré de l’amplitude des déplacements et des fréquences, chaque instrument a une limite supérieure d’amplitude dans la perturbation physique. »
— F. Wu et P. Pério, « La phase en acoustique musicale I. Analyse d’un signal quasi périodique », Le journal de Physique, t. 40, no 8, août 1979[12]
Un harmonique est un membre de la série harmonique, formée de partiels de fréquences multiples entiers positifs d'une fréquence fondamentale commune. La fondamentale est comptée elle-même parmi les membres de la série. Un partiel harmonique est une composante partielle réelle d'un son complexe qui correspond approximativement à une harmonique idéale[13].
Un partiel inharmonique est un partiel qui ne correspond pas à un harmonique idéal. L'inharmonicité est une mesure de l'écart d'un partiel par rapport à l'harmonique idéal le plus proche, généralement mesurée en cents pour chaque partiel[14].
De nombreux instruments acoustiques à hauteur définie sont conçus pour avoir des partiels qui sont proches de rapports de nombres entiers avec une inharmonicité très faible ; par conséquent, en théorie de la musique et dans la conception des instruments, il est commode, bien que pas strictement exact, de parler des partiels dans les sons de ces instruments comme « harmoniques », même s'ils peuvent avoir un certain degré d'inharmonicité. Le piano, l'un des instruments les plus importants de la tradition occidentale, contient un certain degré d'inharmonicité parmi les fréquences produites par chaque corde. D'autres instruments à hauteur, en particulier certains instruments de percussion, tels que le marimba, le vibraphone, les cloches tubulaires, les timbales et les bols chantants, contiennent principalement des partiels inharmoniques, mais peuvent donner à l'oreille une bonne idée de la hauteur grâce à quelques partiels forts qui ressemblent à des harmoniques. Les instruments à hauteur non marquée, ou à hauteur indéterminée, tels que les cymbales et les tam-tams produisent des sons (spectres) riches en sons partiels inharmoniques et ne donnent pas l'impression d'impliquer une hauteur de son particulière.
Un partiel correspond à toute composante du son analysé. La puissance relative des différents partiels (harmoniques ou non) contribue au timbre d'un instrument, sa couleur sonore ou son caractère particulier[b]. Lorsqu'on écrit ou parle d'harmoniques et de partiels numériquement, il faut veiller à les désigner correctement pour éviter toute confusion de l'un avec l'autre : « Parce que les autres partiels sont plus hauts que le son fondamental qui donne au Clang (i.e. son complexe) son nom, on les appelle généralement overtones (en français : « partiel »)[15]. »
Certains instruments électroniques, tels que les synthétiseurs, peuvent jouer une fréquence pure sans composante (une onde sinusoïdale). Les synthétiseurs peuvent également combiner des sons purs pour obtenir des sons plus complexes, par exemple pour émuler d'autres instruments. Certaines flûtes et certains ocarinas sont pratiquement dépourvus d'harmoniques.
Hermann von Helmholtz décrit les partiels harmoniques comme suit :
« L'oreille n'entend pas seulement ce son dont la hauteur est déterminée par la période des vibrations, mais elle entend en plus de ceux-ci toute une série de sons plus élevés, que nous appelons les partiels harmoniques du son complexe (Klang), en opposition avec ce premier son, le son fondamental, qui est le plus grave et généralement le plus puissant et à partir de la hauteur duquel nous jugeons celle du son complexe tout entier. La série de ces partiels est précisément la même pour tous les sons complexes musicaux qui correspondent à un mouvement périodique uniforme de l'air. »
— Hermann von Helmholtz, Die Lehre von dem Tonempfindungen, 4e édition, 1877, p. 37.
Systèmes d'exemples

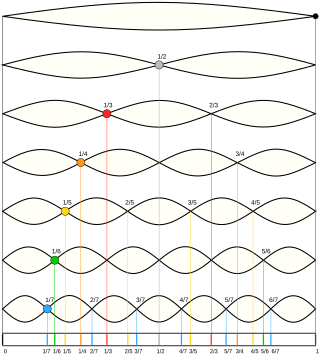
L'un des cas les plus simples à visualiser est celui d'une corde vibrante, comme dans l'illustration ; la corde a des points fixes à chaque extrémité. De ce fait, la plus grande longueur d'onde autorisée sur la corde (qui donne la fréquence fondamentale) est le double de la longueur de la corde : un aller-retour, avec un demi-cycle entre les nœuds aux deux extrémités (non représenté sur l'illustration). Les autres longueurs d'onde possibles sont celles qui respectent les extrémités fixes, c'est-à-dire des fractions entières de la fondamentale : 1⁄2, 1⁄3, 1⁄4 (l'illustration ne présente que les harmoniques de rang pair). Ces longueurs d'onde plus courtes correspondent théoriquement à des vibrations à des fréquences multiples entières (par exemple 2, 3, 4 fois) de la fréquence fondamentale. Les caractéristiques physiques du milieu vibrant et/ou du résonateur contre lequel il vibre modifient souvent ces fréquences. (Voir inharmonicité et accord étiré (en) pour les altérations spécifiques aux instruments à cordes métalliques et à certains pianos électriques). Cependant, ces altérations sont minimes et, sauf dans le cas de nécessité d'un accordage précis et hautement spécialisé, il est raisonnable de considérer les fréquences de la série harmonique comme des multiples entiers de la fréquence fondamentale.
Des arguments similaires s'appliquent aux colonnes d'air vibrantes des instruments à vent (par exemple, "le cor d'harmonie était à l'origine un instrument sans valve qui ne pouvait jouer que les notes de la série harmonique"[16] ou aussi cor naturel), bien qu'elles puissent être compliquées par la possibilité d'anti-nœuds (c'est-à-dire que la colonne d'air est fermée à une extrémité et ouverte à l'autre), une forme conique, les perces, ou des ouvertures d'extrémité qui vont du gamut à l'absence d'évasement, à l'évasement conique ou à l'évasement de forme exponentielle (comme dans les différents pavillons).
Ainsi, avec la plupart des instruments de musique, la fondamentale (premier partiel) est accompagnée d'autres harmoniques de fréquence plus élevée, qui apparaissent avec une proéminence variable et donnent à chaque instrument sa signature sonore caractéristique.
La série harmonique est une progression arithmétique (f, 2f, 3f, 4f, 5f,...). En termes de fréquence (mesurée en cycles par seconde, ou hertz, où f est la fréquence de la fondamentale), la différence entre deux harmoniques consécutifs est donc constante et égale à la fondamentale (f). Mais comme l'oreille humaine réagit au son non linéairement, les harmoniques supérieurs sont perçus comme « plus proches » que les inférieurs. La série des octaves quant à elle est une progression géométrique (2f, 4f, 8f, 16f,...), et les gens perçoivent ces distances comme « équivalent » au sens d'intervalle musical. En termes d'audition, chaque octave de la série harmonique est divisée en intervalles de plus en plus « petits » et de plus en plus nombreux.
Le deuxième harmonique, dont la fréquence est le double de la fondamentale, sonne une octave plus haut ; le troisième harmonique, dont la fréquence est le triple de la fondamentale, sonne une quinte juste au-dessus de la deuxième harmonique. Le quatrième harmonique vibre à quatre fois la fréquence de la fondamentale et sonne une quarte juste au-dessus du troisième harmonique (deux octaves au-dessus de la fondamentale). Le double du nombre d'harmoniques signifie le double de la fréquence (qui sonne une octave plus haut).
- Illustration en notation musicale de la série harmonique (sur do) jusqu'au 20e harmonique. Les nombres au-dessus de l'harmonique indiquent la différence en cents par rapport au tempérament égal (arrondi à l'entier le plus proche). Les notes bleues sont très bémolisées et les notes rouges sont très augmentées. Les auditeurs habitués à un accord plus tonal (en), tel que le tempérament mésotonique et les tempéraments bien tempérés, remarquent que beaucoup d'autres notes sont « décalées ».
- Harmoniques sur le do, du 1er (fondamental) au 32e harmonique (cinq octaves plus haut). La notation utilisée est basée sur la notation dénommée « intonation juste étendue » de Ben Johnston.
- La série harmonique en tant que notation musicale avec les intervalles entre les harmoniques étiquetés. Les notes bleues diffèrent le plus significativement du tempérament égal. On peut écouter A2 (110 Hz) et 15 de ses partiels.
- Notation des partiels 1, 3, 5, 7, 11, 13, 17, et 19 sur do. Ce sont des « nombres premiers harmoniques »[17]..
Marin Mersenne (1588-1648) a écrit : « L'ordre des Consonances est naturel, et [...] la manière dont nous les comptons, depuis l'unité jusqu'au nombre six et au delà, est fondée sur la nature[18]. » Cependant, pour citer Carl Dahlhaus, « l'intervalle-distance de la rangée des tons naturels partiels [...], comptant jusqu'à 20, comprend tout ce qui va de l'octave au quart de ton, (et) des tons musicaux utiles et inutiles. La série harmonique des tons naturels justifie tout, c'est-à-dire rien[19]. »
Harmoniques et accordage
Si les harmoniques sont déplacés d'une octave et transposés dans l'espace d'une octave, certains d'entre eux sont approximés par les notes de ce que l'Occident a adopté comme échelle chromatique basée sur le ton fondamental. La gamme chromatique occidentale a été modifiée en douze demi-tons égaux, ce qui est légèrement désaccordé avec de nombreux harmoniques, en particulier les 7e, 11e et 13e harmoniques. À la fin des années 1930, le compositeur Paul Hindemith a classé les intervalles musicaux en fonction de leur dissonance relative sur la base de ces relations harmoniques et d'autres similaires[20].
Voici une comparaison entre les 31 premiers harmoniques et les intervalles du tempérament égal à 12 tons (12TET), déplacés d'une octave et comprimés dans l'étendue d'une octave. Les champs teintés mettent en évidence les différences supérieures à 5 cents (1⁄20 d'un demi-ton), ce qui correspond au « seuil de discrimination » de l'oreille humaine pour des notes jouées l'une après l'autre (des différences plus petites sont perceptibles avec des notes jouées simultanément).
Les fréquences de la série harmonique, étant des multiples entiers de la fréquence fondamentale, sont naturellement liées les unes aux autres par des rapports de nombres entiers et les petits rapports de nombres entiers sont probablement à la base de la consonance des intervalles musicaux (voir intonation juste). Cette structure objective est renforcée par des phénomènes psychoacoustiques. Par exemple, une quinte juste, disons aux fréquences de 200 et de 300 Hz, fait qu'un auditeur perçoit un son résultant de 100 Hz (soit la différence entre 300 Hz et 200 Hz) ; c'est-à-dire une octave en dessous de la note la plus grave (cette fréquence est bien celle du son complexe que forme la superposition des deux vibrations, mais l'analyse spectrale n'y trouve aucun partiel, c'est-à-dire une fréquence pour laquelle on trouve une puissance). Ce son résultant de premier ordre de 100 Hz (fréquence de battement) interagit ensuite avec les deux notes de l'intervalle pour produire des sons résultants de deuxième ordre de 200 (300 − 100) et de 100 (200 − 100) Hz et tous les autres sons combinés de troisième ordre sont tous identiques, étant formés à partir de diverses soustractions de 100, 200 et 300. Si l'on oppose à cela un intervalle dissonant tel qu'un triton (non tempéré) avec un rapport de fréquence de 7:5, on obtient, par exemple, 700 − 500 = 200 (son de combinaison de 1er ordre) et 500 − 200 = 300 (2e ordre). Les autres sons combinés sont des octaves de 100 Hz.
Tous les intervalles succombent à une analyse similaire, comme l'a démontré Paul Hindemith dans son livre The Craft of Musical Composition, bien qu'il ait rejeté l'utilisation des harmoniques à partir de la septième et au-delà[20].
Le mode mixolydien est consonant avec les 10 premiers harmoniques de la série harmonique (le 11e harmonique, un triton, n'est pas dans le mode mixolydien). Le mode ionien n'est consonant qu'avec les 6 premiers harmoniques de la série (le septième harmonique, une septième mineure, n'est pas dans le mode ionien). Le Rishabhapriya ragam (en) est consonant avec les 14 premiers harmoniques de la série.
Puissance de l'intervalle
David Cope (1997) suggère le concept de force de l'intervalle[21] dans lequel la force, la consonance ou la stabilité d'un intervalle (voir consonance et dissonance) est déterminée par son approximation à une position plus basse et plus forte, ou plus haute et plus faible, dans la série harmonique. Voir aussi : Loi de Lipps-Meyer (en).
Ainsi, une quinte juste tempérée égale (ⓘ) est plus forte qu'une tierce mineure tempérée égale (ⓘ), puisqu'elles se rapprochent respectivement d'une quinte juste parfaite (ⓘ) et d'une tierce juste mineure (ⓘ). La tierce mineure apparaît entre les harmoniques 5 et 6, tandis que la quinte juste apparaît plus bas, entre les harmoniques 2 et 3.
Remove ads
Annexes
Résumé
Contexte
Grammaire
Harmonique est à l'origine un adjectif qualifiant des grandeurs qui sont multiples d'une même valeur, dite fondamentale. Dans l'étude des vibrations, les partiels qui ne sont pas harmoniques sont dits inharmoniques. Seuls les partiels harmoniques contribuent à l'identification de la note de musique.
Employé comme substantif, il remplace l'expression « partiel harmonique ». Il est par conséquent, comme partiel, du genre masculin.
Si, dans un discours, on utilisait harmonique comme substantif pour remplacer « note harmonique » ou « division harmonique », il serait du genre féminin, comme les substantifs de l'expression à laquelle il se substituerait[réf. souhaitée].
Par contamination du substantif féminin harmonie, il s'emploie aussi au féminin[22].
Bibliographie
- Patrice Bailhache, Antonia Soulez et Céline Vautrin, Helmholtz du son à la musique, Paris, Librairie philosophique J. Vrin, , 253 p. (ISBN 978-2-7116-2337-2, lire en ligne)
- Philippe Gouttenoire et Jean-Philippe Guye, Vocabulaire pratique d'analyse musicale, Delatour france, , 128 p. (ISBN 978-2-7521-0020-7)
- André Calvet (préf. Franck Jedrzejewski), Le Clavier Bien Obtempéré. Essai de Tempéramentologie, Montpellier, Piano e forte éditions, , 470 p.
- (en) Hugo Riemann (trad. de l'allemand par John South Shedlock), Dictionary of Music [« Musiklexikon »], London, Augener & Co,
- (en) Manuel Op de Coul, « List of intervals (Compiled) », Huygens-Fokker Foundation centre for microtonal music (consulté le ).
- (en) A. K. Datta, R. Sengupta,, N. Dey et D. Nag, Experimental Analysis of Shrutis from Performances in Hindustani Music, Kolkata, India, SRD ITC SRA, (ISBN 81-903818-0-6, lire en ligne), p. I-X, 1–103.
- (de) Hermann von Helmholtz, Die Lehre von dem Tonempfindungen. Zweite ausgabe, Braunschweig, Vieweg und Sohn, (lire en ligne), p. I–XII, 1–606 (voir l'ouvrage Sensations of Tone).
- (en) IEV, « Electropedia: The World's Online Electrotechnical Vocabulary », Commission électrotechnique internationale, (consulté le ).
- (en) Horace Lamb et Hugh Chisholm (dir.), « Harmonic Analysis », dans Encyclopædia Britannica 1911, vol. 12, Londres, , 11e éd. (lire sur Wikisource), p. 956-958.
- (en) Harry Partch, Genesis of a Music: An Account of a Creative Work, Its Roots, and Its Fulfillments, New York, Da Capo Press, , 2nd enlarged éd. (ISBN 0-306-80106-X, lire en ligne).
- (en) Jan Frederik Schouten, The residue, a new component in subjective sound analysis, Eindhoven, Holland, Natuurkundig Laboratorium der N. V. Philips' Gloeilampenfabrieken (communicated by Prof. G. Holst at the meeting), (lire en ligne), p. 356–65.
- (ru) Волконский, Андрей Михайлович, ru:Основы темперации, Композитор, Москва, (ISBN 5-85285-184-1, lire en ligne).
- (ru) Юрий Николаевич Тюлин et Беспалова, Н. (dir.) (trad. The teaching on harmony), ru:Учение о гармонии, Moscow, Музыка, .
Articles connexes
Liens externes
Remove ads
Notes et références
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads