Composition (combinatoire)

En mathématiques, et notamment en combinatoire, une composition d'un entier strictement positif ${\displaystyle n}$ est une représentation de ${\displaystyle n}$ comme somme d'une suite finie d'entiers strictement positifs. Ainsi, (1, 2, 1) est une composition de 4=1+2+1. Deux suites qui diffèrent par l'ordre de leurs éléments sont considérées comme des compositions différentes. Ainsi, (2, 1, 1) est une autre composition de l'entier 4. Les compositions diffèrent donc des partitions d'entiers qui considèrent des sommes sans tenir compte de l'ordre de leurs termes.

Bijection entre entiers en écriture binaire et compositions de 4.

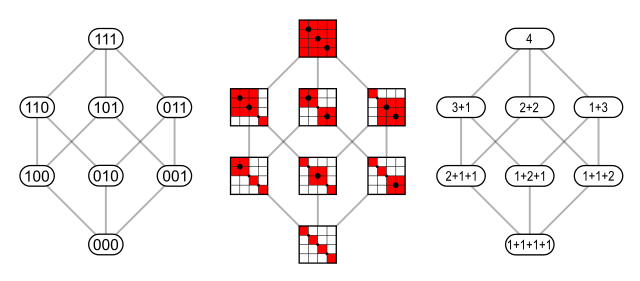
La propriété principale est que le nombre de compositions d'un entier ${\displaystyle n}$ est égal à ${\displaystyle 2^{n-1}}$, et donc que les compositions sont en bijection avec les parties d'un ensemble à ${\displaystyle n-1}$ éléments.

Définition

Une composition d'un entier naturel positif ${\displaystyle n>0}$ est une suite ${\displaystyle (p_{1},\ldots ,p_{k})}$ d'entiers strictement positifs tels que ${\displaystyle n=p_{1}+\cdots +p_{k}}$. Chaque ${\displaystyle p_{i}}$ est appelé une partie, part ou sommant de la composition et l'entier ${\displaystyle k}$ est sa longueur.

Exemples

Les 32 compositions de 6. L'absence d'une barre de séparation est notée en rouge.

Les 11 partitions de 6. Une partition est une composition dont les parts sont décroissantes.

Le nombre 5 possède seize compositions :

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 3
• 2 + 2 + 1
• 2 + 1 + 2
• 2 + 1 + 1 + 1
• 1 + 4
• 1 + 3 + 1
• 1 + 2 + 2
• 1 + 2 + 1 + 1
• 1 + 1 + 3
• 1 + 1 + 2 + 1
• 1 + 1 + 1 + 2
• 1 + 1 + 1 + 1 + 1,

et seulement sept partitions :

• 5
• 4 + 1
• 3 + 2
• 3 + 1 + 1
• 2 + 2 + 1
• 2 + 1 + 1 + 1
• 1 + 1 + 1 + 1 + 1.

Dénombrement des compositions

De façon imagée, le nombre de compositions de l'entier ${\displaystyle n}$ est le nombre de façons de vider un tonneau de n litres à l'aide de récipients de contenance un nombre entier de litres, ou le nombre de façons de découper un segment de longueur n en segments de longueur entière.

Le nombre de composition de l’entier ${\displaystyle n}$ est égal à ${\displaystyle 2^{n-1}}$.

Démonstration par la méthode des étoiles et des barres

Voici une démonstration de cette propriété utilisant la méthode des étoiles et des barres. On considère une suite de ${\displaystyle n}$ points (ou étoiles), et on choisit de placer ou de ne pas placer une barre verticale entre des points. Par exemple, pour ${\displaystyle n=8}$, on peut placer trois barres comme suit :

${\displaystyle \bullet \,\,\,\bullet \mid \bullet \,\,\,\bullet \mid \bullet \mid \bullet \,\,\,\bullet \,\,\,\bullet }$

Chaque ensemble de points contigus forme une part de la composition. Dans l'exemple, la composition est égale à (2, 2, 1, 3). De manière générale, il y a ${\displaystyle n-1}$ positions où l'on peut choisir de placer ou de ne pas placer une barre de séparation ; ceci fait ${\displaystyle 2^{n-1}}$ choix possibles de séparations et comme les choix déterminent les compositions, cela fait ${\displaystyle 2^{n-1}}$ compositions^[1].

La démonstration montre aussi que le nombre de compositions d'un entier ${\displaystyle n}$ formées de ${\displaystyle k}$ parts est égal à ${\displaystyle {\binom {n-1}{k-1}}}$.

Bijection avec les écritures binaires

Pour noter la représentation graphique ci-dessus, on peut convenir d'écrire un « 1 » s'il n'y a pas de barre de séparation, et un « 0 » dans le cas contraire. Ainsi, la composition (2, 2, 1, 3) de 8 est représentée par la suite de 8 chiffres binaires 1010011 (il y a autant de 0 dans « 1010011 » qu'il y a de virgules dans « (2, 2, 1, 3) »). Les compositions sont donc en bijection avec les mots binaires de longueur ${\displaystyle n-1}$.

Démonstration par relation de récurrence

Si ${\displaystyle u_{n}}$ désigne le nombre de compositions de l'entier ${\displaystyle n}$, le nombre de compositions se terminant par 1 vaut ${\displaystyle u_{n-1}}$, se terminant par 2 vaut ${\displaystyle u_{n-2}}$, etc. Donc ${\displaystyle u_{n}=u_{n-1}+u_{n-2}+\cdots +u_{1}+1}$ ; de même ${\displaystyle u_{n-1}=u_{n-2}+\cdots +u_{1}+1}$, donc ${\displaystyle u_{n}=2u_{n-1}}$ ; comme ${\displaystyle u_{1}=1}$, ${\displaystyle u_{n}=2^{n-1}}$.

Remarque : posant ${\displaystyle u_{0}=1}$, la suite ${\displaystyle (u_{n})}$ est définie par la donnée de son premier terme, et le fait que tout terme est la somme de tous les précédents, d'où son appellation de suite d'infinacci.

Dénombrements de compositions particulières

Le nombre ${\displaystyle v_{n}}$de compositions de ${\displaystyle n}$ ne comportant que des 1 et des 2 (de façon imagée le nombre de façons de vider un tonneau de ${\displaystyle n}$ litres avec des bouteilles de 1 ou 2 litres) vérifie ${\displaystyle v_{n}=v_{n-1}+v_{n-2}}$ (cf. raisonnement ci-dessus). Comme ${\displaystyle v_{1}=1,v_{2}=2}$, ${\displaystyle v_{n}=F_{n+1}}$ où ${\displaystyle (F_{n})}$ est la suite de Fibonacci.

Plus généralement le nombre de compositions de ${\displaystyle n}$ formées à partir des entiers de 1 à ${\displaystyle p}$ est la suite de p-bonacci décalée.

Notes

Les compositions d'entiers sont un objet combinatoire simple, et se trouvent dans de nombreux livres de combinatoire de base. Louis Comtet en parle dans le premier volume de son livre^[2]. Knuth^[3] y consacre une section. Un ouvrage entier a été consacré aux compositions et à ses variantes^[4]. Donald Knuth, dans le volume 4a de son traité^[3], s'intéresse à la génération de toutes les compositions, sous des contraintes variées.