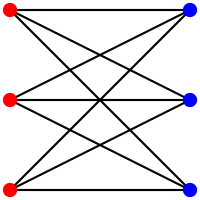
Graphe biparti

En théorie des graphes, un graphe est dit biparti si son ensemble de sommets peut être divisé en deux sous-ensembles disjoints ${\displaystyle U}$ et ${\displaystyle V}$ tels que chaque arête ait une extrémité dans ${\displaystyle U}$ et l'autre dans ${\displaystyle V}$.

Exemple de graphe biparti quelconque

Un graphe biparti permet notamment de représenter une relation binaire.

Caractérisation

Il existe plusieurs façons de caractériser un graphe biparti.

Par le nombre chromatique

Les graphes bipartis sont les graphes dont le nombre chromatique est inférieur ou égal à 2.

Par la longueur des cycles

Un graphe est biparti si et seulement s'il ne contient pas de cycle impair^[1].

Démonstration

Supposons qu'un graphe est décomposé en deux partitions ${\displaystyle U}$ et ${\displaystyle V}$ telles que toute arête relie un sommet de ${\displaystyle U}$ à un sommet de ${\displaystyle V}$. Considérons un cycle quelconque. Ce cycle passe alternativement par les deux parties ${\displaystyle U}$ et ${\displaystyle V}$ avant de rejoindre le sommet de départ et a donc une longueur paire.

Construction des deux partitions dans un graphe ne comportant que des cycles de longueur paire : l'arbre couvrant est en rouge, on colore les sommets en bleu et blanc alternativement depuis sa racine ${\displaystyle r}$.

La réciproque est quelque peu plus dure à démontrer. Supposons que l'on ait un graphe ${\displaystyle G}$ qui ne comporte que des cycles de longueur paire. Pour simplifier, supposons également que ${\displaystyle G}$ est connexe (si jamais il ne l'était pas, on pourrait raisonner individuellement sur chaque composante connexe).

Comme ${\displaystyle G}$ est connexe, il possède un arbre couvrant ${\displaystyle T}$. Notons ${\displaystyle r}$ une racine de cet arbre. Créons deux ensembles de sommets ${\displaystyle U}$ et ${\displaystyle V}$ de la manière suivante :

• ${\displaystyle U}$ contient ${\displaystyle r}$ et tous les sommets de ${\displaystyle T}$ se trouvant à un nombre pair d'arêtes de ${\displaystyle r}$ ;
• ${\displaystyle V}$ contient les sommets de ${\displaystyle T}$ se trouvant à un nombre impair d'arêtes de ${\displaystyle r}$.

Les ensembles de sommets ${\displaystyle U}$ et ${\displaystyle V}$ sont disjoints et contiennent tous les sommets de ${\displaystyle G}$. Cela ne suffit cependant pas à montrer que ${\displaystyle G}$ est biparti : en effet, rien ne garantit a priori que l'on n'ait pas une arête « en trop » de ${\displaystyle G}$ qui relie deux sommets de ${\displaystyle U}$, par exemple.

Considérons deux sommets ${\displaystyle x}$ et ${\displaystyle y}$ de ${\displaystyle G}$ dans une même partie (${\displaystyle U}$ ou ${\displaystyle V}$) et reliés par une arête ${\displaystyle e}$. Le chemin qui relie ${\displaystyle x}$ à ${\displaystyle y}$ dans ${\displaystyle T}$ est forcément de longueur paire, par construction de ${\displaystyle U}$ et de ${\displaystyle V}$. Si l'on ajoute l'arête ${\displaystyle e}$, on obtient un cycle de longueur impaire, ce qui est interdit par hypothèse.

Il n'est donc pas possible d'avoir de tels sommets ${\displaystyle x}$ et ${\displaystyle y}$ reliés en « court-circuit ». Toutes les arêtes du graphe relient des sommets de ${\displaystyle U}$ à des sommets de ${\displaystyle V}$, ce qui achève de montrer que ${\displaystyle G}$ est biparti.

Par le spectre

Si un graphe est biparti, alors son spectre vérifie la propriété suivante^[2] :

Si ${\displaystyle \lambda }$ est une valeur propre de la matrice d'adjacence du graphe, alors ${\displaystyle -\lambda }$ en est aussi une, avec la même multiplicité que celle de ${\displaystyle \lambda }$.

Par les polyèdres

Un graphe est biparti si et seulement si son polytope des stables est décrit par les contraintes de clique de taille 2.

Graphes bipartis particuliers

Exemple de graphe biparti complet

Les graphes suivants sont bipartis : le graphe vide, les arbres, les cycles de longueurs paires, les hypercubes et les grilles.

De plus, on définit les graphes bipartis suivants :

• Un graphe biparti est dit biparti complet (ou encore est appelé une biclique) si chaque sommet de ${\displaystyle U}$ est relié à chaque sommet de ${\displaystyle V}$.
• Un graphe biparti est dit birégulier si tous les sommets de ${\displaystyle U}$ ont le même degré, et si tous les sommets de ${\displaystyle V}$ ont le même degré.
• Les graphes bipartis de Kneser sont une famille de graphes bipartis permettant de décrire des relations d'inclusion entre ensembles.
• 110-graphe de Iofinova-Ivanov