Produit tensoriel (graphe)

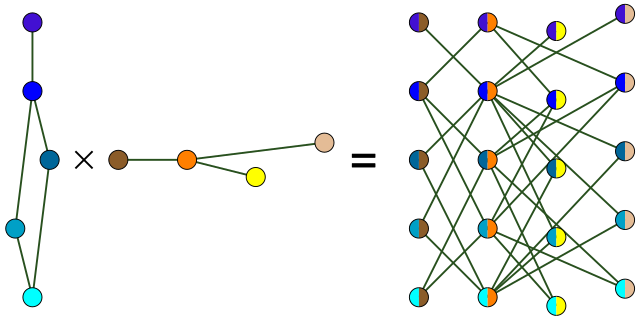
Le produit tensoriel est une opération sur deux graphes ${\displaystyle G}$ et ${\displaystyle H}$ résultant en un graphe ${\displaystyle G\times H}$. Il est également appelé produit direct, produit de Kronecker ou produit catégorique.

Produit tensoriel de deux graphes.

Construction

Soient deux graphes ${\displaystyle G}$ et ${\displaystyle H}$. Le produit tensoriel ${\displaystyle G\times H}$ est défini comme suit^[1] :

• l'ensemble de ses sommets est le produit cartésien ${\displaystyle V(G)\times V(H)}$ ;
• ${\displaystyle (g,h)}$ et ${\displaystyle (g',h')}$ sont adjacents dans ${\displaystyle G\times H}$ si et seulement si ${\displaystyle g}$ et ${\displaystyle g'}$ sont adjacents dans ${\displaystyle G}$ et ${\displaystyle h}$ et ${\displaystyle h'}$ sont adjacents dans ${\displaystyle H}$. Autrement dit, deux sommets sont voisins si les sommets dont ils sont issus étaient voisins dans les deux graphes.

Propriétés

• La matrice d'adjacence de ${\displaystyle G\times H}$ est le produit de Kronecker des matrices d'adjacence de ${\displaystyle G}$ et ${\displaystyle H}$.
• La conjecture d'Hedetniemi (en) concernait le nombre chromatique du produit tensoriel de deux graphes : ${\displaystyle \chi (G\times H)\;{\overset {?}{=}}\;\min\{\chi (G),\chi (H)\}}$. Elle est cependant réfutée en 2019 par Yaroslav Shitov qui montre qu'il est possible d'avoir ${\displaystyle \chi (G\times H)<\min\{\chi (G),\chi (H)\}}$^[2].