Ensemble vide

En mathématiques, l'ensemble vide est l'ensemble ne contenant aucun élément.

Un symbole qui représente l'ensemble vide.

Notation

Autre notation de l'ensemble vide.

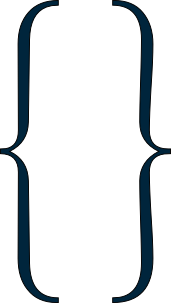
L'ensemble vide peut être noté d'un O barré^[1], à savoir ∅ ou simplement { }, qui est une paire d'accolades ne contenant qu'une espace, pour représenter un ensemble qui ne contient rien. La notation ∅ a été introduite par André Weil, dans le cadre de l'institution de notations par le groupe Bourbaki^[2]. Von Neumann dans son article de 1923^[3],[4], qui est l'une des premières références qui l'aborde, le note O.

Exemples

Les ensembles ${\displaystyle \{n\in \mathbb {Z} \mid 0<n<1\}}$ et ${\displaystyle \{n\in {\mathbb {Z}}\mid n^{2}=-1\}}$ sont tous deux égaux à l'ensemble vide^[5].

Propriétés

Propriétés en lien avec les opérations ensemblistes

Pour tout ensemble A :

• l'ensemble vide est un sous-ensemble de A :∅ ⊂ A ;
• l'union de A avec l'ensemble vide est A :

  ∅ ∪ A = A ∪ ∅ = A,

  soit : l'ensemble vide est élément neutre pour la réunion ;

• l'intersection de A avec l'ensemble vide est l'ensemble vide :

  ∅ ∩ A = A ∩ ∅ = ∅,

  soit : l'ensemble vide est élément absorbant pour l'intersection ;

• le seul sous-ensemble de l'ensemble vide est l'ensemble vide lui-même :

  A ⊂ ∅ ⇔ A = ∅,

  donc l'ensemble des parties de l'ensemble vide est un singleton, dont l'élément est l'ensemble vide : ${\displaystyle {\mathcal {P}}(\varnothing )=\{\varnothing \}}$ ;

• le produit cartésien de A par l'ensemble vide est vide :

  A × ∅ = ∅ × A = ∅,

  soit : l'ensemble vide est élément absorbant pour le produit cartésien ;

• si A est non vide, l'ensemble des applications de A dans l'ensemble vide est vide :

  A ≠ ∅ ⇒ ∅^A = ∅ ;

• l'ensemble des applications de l'ensemble vide dans A est un singleton, dont l'élément est l'« application vide de ∅ dans A » (de graphe ∅)^[6]. Si on la note ∅_A, on a donc :

  A^∅ = {∅_A}.

  Par exemple, {0, 1}^∅ = {∅_{{0, 1}}}, ce qui est cohérent avec l'égalité ${\displaystyle {\mathcal {P}}(\varnothing )=\{\varnothing \}}$ ci-dessus.

Dans le cas d'une famille d'ensembles :

• l'union généralisée indexée par ∅ est égale à ∅ ;
• l'intersection généralisée indexée par ∅ n'est pas définie dans le cas général ie. sans faire référence à un ensemble qui les contient tous, auquel cas elle est égale à ce dernier.

Autres propriétés

L'ensemble vide :

• est unique par extensionnalité (un axiome de la théorie des ensembles qui assure qu'un ensemble est complètement défini par la donnée de tous ses éléments, d'où l'unicité de l'ensemble n'en contenant aucun) ;
• est fini, de cardinal nul ce que l'on note card(∅) = 0 ;
• admet une unique topologie, qui est {∅} : elle est à la fois grossière (donc cet espace topologique est connexe) et discrète (donc il est compact, comme tout espace fini discret) ;
• admet une unique tribu, qui est {∅} (grossière et discrète).

Dans certaines variantes de la théorie des ensembles, on peut introduire des « objets » appelés ur-elements^[7] qui, comme l'ensemble vide, n'ont pas d'éléments et peuvent être éléments d'ensembles mais qui, contrairement à lui, ne sont pas des ensembles.

Subtilité de la notion d’ensemble vide

L'ensemble vide ne contient rien, mais comme c'est un ensemble, il n’est pas rien. C'est la base sur laquelle s'appuie von Neumann^[3],[4] pour construire les entiers et les ordinaux.

La notation {∅} n'a pas le même sens que la notation ∅ ; en effet, l’ensemble désigné par ∅ n'a aucun élément (car c’est l'ensemble vide), tandis que l’ensemble désigné par {∅} en a un (cet élément est l'ensemble vide). D'ailleurs, von Neumann définit 0 comme étant ∅ et 1 comme étant {∅}.

Rappelons (voir supra) que l'ensemble vide est un sous-ensemble de n'importe quel ensemble A, c'est-à-dire que pour tout élément x de ∅, x appartient à A, ce qui s'écrit formellement : (∀x ∈ ∅) x ∈ A. Plus généralement, un énoncé de la forme « tout élément de l'ensemble vide possède la propriété P  », ou plus formellement (∀x ∈ ∅) P(x), qui est une abréviation de ∀x (x ∈ ∅ ⇒ P(x)), est toujours vrai, par ex falso quodlibet ; de même, tout énoncé de la forme «il existe un élément de l'ensemble vide possédant la propriété P  » est toujours faux (ce second résultat est sans doute plus évident, mais ce n'est que la négation de l'affirmation précédente).

L'axiome de fondation affirme que toute suite ${\displaystyle x_{0}\ni x_{1}\ni x_{2}\ldots }$ se termine, donc il existe un ${\displaystyle n}$ tel que, dans cette suite, ${\displaystyle x_{n}=\varnothing }$.

L'ensemble vide dans la théorie axiomatique des ensembles

L'ensemble vide est essentiel dans la théorie des ensembles ou théorie ZFC, son existence est assurée par l'axiome de l'ensemble vide. Son unicité découle de l'axiome d'extensionnalité.

De plus, on peut démontrer en utilisant le schéma d'axiomes de compréhension, que l'existence d'un ensemble quelconque implique l'axiome de l'ensemble vide, ce qui évite, quand on formalise la théorie des ensembles en logique du premier ordre, de faire appel à un axiome spécifique pour l'existence de l'ensemble vide (voir axiome de l'ensemble vide).

Le point de vue intuitionniste

On dit, par définition, qu'un ensemble est habité (en)^[8] s'il a au moins un élément.

Par conséquent :

un ensemble habité est non vide,

Sa réciproque s'énonce ainsi :

un ensemble non vide est habité,

et peut se formuler :

un ensemble qui n'est pas ∅ possède au moins un élément.

Affirmer son équivalence à un ensemble habité est non vide nécessite le tiers exclu et n'est donc pas valide en logique intuitionniste^[9].

On a d'ailleurs le théorème :

• Le principe du tiers exclu est équivalent à l'affirmation tout ensemble non vide est habité^[10]

Le point de vue catégorique

L'ensemble vide peut être caractérisé très simplement comme objet de la catégorie des ensembles. C'est en effet l'unique objet ayant la propriété suivante :

Pour tout ensemble E, il existe une et une seule flèche de ∅ vers E.

Dans le cas de cette catégorie, flèche signifie application. Plus généralement, un objet qui, dans une catégorie, a cette propriété est appelé un objet initial.