Espiral dourada

A espiral dourada (denominada tamén espiral áurea) é unha espiral logarítmica asociada ás propiedades xeométricas do rectángulo dourado.^[1] A razón de crecemento é Φ, é dicir a razón dourada ou número áureo. Aparece esta espiral representada en diversas figuras da natureza (plantas, galaxias espirais), así como na arte.

Espiral áurea construída a partir da evolución dun rectángulo dourado.

As espirais áureas son autosimilares. A forma repítese indefinidamente cando se amplía. (Fractais)

Desenvolvemento matemático

A ecuación polar que describe a espiral dourada é a mesma que calquera outra espiral logarítmica, pero co factor de crecemento (${\displaystyle b}$) igual Φ, isto é:^[2]

${\displaystyle r=ae^{b\theta }\,}$

ou, da mesma forma

${\displaystyle \theta ={\frac {1}{b}}\ln(r/a),}$

Sendo e a base do logaritmo natural, ${\displaystyle a}$ é unha constante real positiva e ${\displaystyle b}$ é tal que cando o ángulo θ é un ángulo recto:

${\displaystyle e^{b\theta _{\mathrm {recto} }}\,=\phi }$

Por tanto, ${\displaystyle b}$ atópase determinado por

${\displaystyle b={\ln {\phi } \over \theta _{\mathrm {recto} }}.}$

O valor numérico de ${\displaystyle b}$ depende de se o ángulo θ é medido en graos ou radiáns; como ${\displaystyle b}$ pode tomar valores positivos ou negativos segundo o signo de θ o máis sinxelo é indicar o seu valor absoluto:

Unha espiral de Fibonacci aproxímase á espiral dourada cando se inscribe en cadrados cuxos lados responden á sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34...

${\displaystyle |b|={\ln {\phi } \over 90}=0.0053468\,}$ para θ en graos

${\displaystyle |b|={\ln {\phi } \over \pi /2}=0.306349\,}$para θ en radiáns

Unha fórmula alternativa para a espiral dourada obtense en:^[3]

${\displaystyle r=ac^{\theta }\,}$

onde a constante ${\displaystyle c}$ está determinada por:

${\displaystyle c=e^{b}\,}$

para a espiral dourada os valores de ${\displaystyle c}$ son:

${\displaystyle c=\phi ^{\frac {1}{90}}\doteq 1.0053611}$

se θ se mide en graos sexaxesimais, e

${\displaystyle c=\phi ^{\frac {2}{\pi }}\doteq 1.358456.}$

se θ se mide en radiáns.

Espirais douradas verdadeiras e aproximadas: a espiral verde está formada por cuartos de circunferencias inscritas en cadrados; a espiral vermella é unha espiral dourada, un tipo particular de espiral logarítmica. Ao solaparse as dúas espirais, obtense a espiral amarela

Aproximacións á espiral dourada

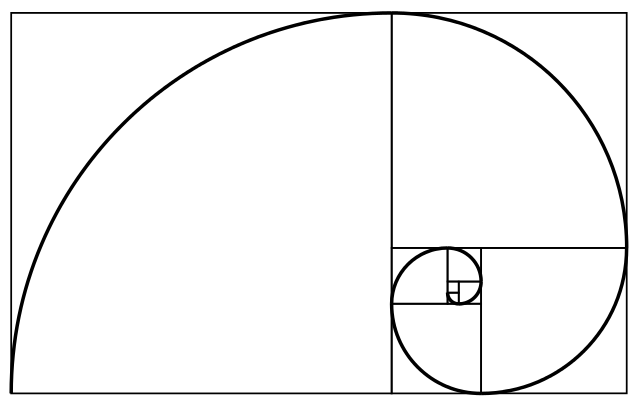
Existen aproximacións á espiral dourada, que non son iguais.^[4] Este tipo de espirais, a miúdo confúndense coa espiral dourada. Un exemplo é a espiral de Fibonacci que resulta ser unha aproximación á espiral dourada.

Galería

• 
  Mediante convolución de rectas
• 
  Cuncha dun Nautilus
• 
  Espiral no triángulo e a súa serie de Fibonacci
• 
  A moeda de ouro máis pequena do mundo