Funcións chan e teito

En matemáticas, a función chan (ou parte enteira cando son positivos) é a función que toma como entrada un número real x, e dá como saída o maior enteiro menor ou igual a x, denotado ⌊x⌋. Do mesmo xeito, a función teito mapea x co número enteiro máis pequeno maior ou igual que x, denotado ⌈x⌉. ^[1]

Funcións chan e teito

Función chan

Función teito

Por exemplo, para o chan: ⌊2.4⌋ = 2, ⌊−2.4⌋ = −3, e para o teito: ⌈4.4⌉ = 5 e ⌈−4.4⌉ = −4.

Exemplos

x	Piso ⌊x⌋	Teito ⌈x⌉	Parte fraccional {x}
2	2	2	0
2.0001	2	3	0,0001
2.4	2	3	0,4
2.9	2	3	0,9
2.999	2	3	0,999
− 2.7	− 3	− 2	0,3
− 2	− 2	− 2	0

Notación

A parte enteira ou parte enteira dun número (partie entière no orixinal) foi definido por primeira vez en 1798 por Adrien-Marie Legendre na súa proba da fórmula de Legendre.

A parte fracciónal denótase por {x} para x real e definida pola fórmula

{x} = x − ⌊x⌋^[2]

Para todo x,

0 ≤ {x} < 1.

No sistema LaTeX, estes símbolos pódense especificar coas palabras \lceil, \rceil, \lfloor e \rfloor.

Definición e propiedades

Dados os números reais x e y, os enteiros m e n e o conxunto de números enteiros ${\displaystyle \mathbb {Z} }$, chan e teito poden ser definidos polas ecuacións

${\displaystyle \lfloor x\rfloor =\max\{m\in \mathbb {Z} \mid m\leq x\},}$

${\displaystyle \lceil x\rceil =\min\{n\in \mathbb {Z} \mid n\geq x\}.}$

Equivalencias

Estas fórmulas pódense usar para simplificar expresións que inclúen chan e teito. ^[3]

${\displaystyle {\begin{alignedat}{3}\lfloor x\rfloor &=m\ \ &&{\mbox{ se e só se }}&m&\leq x<m+1,\\\lceil x\rceil &=n&&{\mbox{ se e só se }}&\ \ n-1&<x\leq n,\\\lfloor x\rfloor &=m&&{\mbox{ se e só se }}&x-1&<m\leq x,\\\lceil x\rceil &=n&&{\mbox{ se e só se }}&x&\leq n<x+1.\end{alignedat}}}$

Para enteiros n temos:

${\displaystyle {\begin{aligned}\lfloor x+n\rfloor &=\lfloor x\rfloor +n,\\\lceil x+n\rceil &=\lceil x\rceil +n,\\\{x+n\}&=\{x\}.\end{aligned}}}$

Para x e y reais temos as seguintes desigualdades:

${\displaystyle {\begin{aligned}\lfloor x\rfloor +\lfloor y\rfloor &\leq \lfloor x+y\rfloor \leq \lfloor x\rfloor +\lfloor y\rfloor +1,\\[3mu]\lceil x\rceil +\lceil y\rceil -1&\leq \lceil x+y\rceil \leq \lceil x\rceil +\lceil y\rceil .\end{aligned}}}$

Monótonas

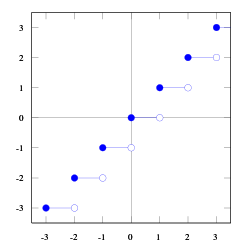
Tanto as funcións chan como teito son funcións monótonamente non decrecentes:

${\displaystyle {\begin{aligned}x_{1}\leq x_{2}&\Rightarrow \lfloor x_{1}\rfloor \leq \lfloor x_{2}\rfloor ,\\x_{1}\leq x_{2}&\Rightarrow \lceil x_{1}\rceil \leq \lceil x_{2}\rceil .\end{aligned}}}$

Relacións entre as funcións

${\displaystyle \lfloor x\rfloor \leq \lceil x\rceil ,}$ con igualdade se e só se x é un número enteiro, é dicir

${\displaystyle \lceil x\rceil -\lfloor x\rfloor ={\begin{cases}0&{\mbox{ if }}x\in \mathbb {Z} \\1&{\mbox{ if }}x\not \in \mathbb {Z} \end{cases}}}$

Ao negar o argumento muda o chan e o teito e mudao signo:

${\displaystyle {\begin{aligned}\lfloor x\rfloor +\lceil -x\rceil &=0\\-\lfloor x\rfloor &=\lceil -x\rceil \\-\lceil x\rceil &=\lfloor -x\rfloor \end{aligned}}}$

e:

${\displaystyle \lfloor x\rfloor +\lfloor -x\rfloor ={\begin{cases}0&{\text{if }}x\in \mathbb {Z} \\-1&{\text{if }}x\not \in \mathbb {Z} ,\end{cases}}}$

${\displaystyle \lceil x\rceil +\lceil -x\rceil ={\begin{cases}0&{\text{if }}x\in \mathbb {Z} \\1&{\text{if }}x\not \in \mathbb {Z} .\end{cases}}}$

A negación do argumento complementa a parte fraccional:

${\displaystyle \{x\}+\{-x\}={\begin{cases}0&{\text{if }}x\in \mathbb {Z} \\1&{\text{if }}x\not \in \mathbb {Z} .\end{cases}}}$

As funcións chan, teito e parte fraccional son idempotentes:

${\displaystyle {\begin{aligned}{\big \lfloor }\lfloor x\rfloor {\big \rfloor }&=\lfloor x\rfloor ,\\{\big \lceil }\lceil x\rceil {\big \rceil }&=\lceil x\rceil ,\\{\big \{}\{x\}{\big \}}&=\{x\}.\end{aligned}}}$

O resultado das funcións aniñadas chan ou teito é a función máis interna:

${\displaystyle {\begin{aligned}{\big \lfloor }\lceil x\rceil {\big \rfloor }&=\lceil x\rceil ,\\{\big \lceil }\lfloor x\rfloor {\big \rceil }&=\lfloor x\rfloor .\end{aligned}}}$

constante de Euler gamma (${\displaystyle \gamma }$)

Existen fórmulas para a constante de Euler ${\displaystyle \gamma }$ = 0,57721 56649... que inclúen o chan e o teito, por exemplo ^[4]

${\displaystyle \gamma =\int _{1}^{\infty }\left({1 \over \lfloor x\rfloor }-{1 \over x}\right)\,dx.}$

${\displaystyle \gamma =\lim _{n\to \infty }{\frac {1}{n}}\sum _{k=1}^{n}\left(\left\lceil {\frac {n}{k}}\right\rceil -{\frac {n}{k}}\right).}$

Fórmulas para números primos

A función chan aparece en varias fórmulas que caracterizan os números primos. Por exemplo, xa que ${\textstyle {\bigl \lfloor }{\frac {n}{m}}{\bigr \rfloor }-{\bigl \lfloor }{\frac {n-1}{m}}{\bigr \rfloor }}$ é igual a 1 se m divide n, e a 0 en caso contrario, dedúcese que un enteiro positivo n é primo se e só se ^[5]

${\displaystyle \sum _{m=1}^{\infty }\left({\biggl \lfloor }{\frac {n}{m}}{\biggr \rfloor }-{\biggl \lfloor }{\frac {n-1}{m}}{\biggr \rfloor }\right)=2.}$

Problemas resolvidos

Ramanujan presentou estes problemas ao Journal of the Indian Mathematical Society. ^[6]

Se n é un número enteiro positivo, proba que

1. ${\displaystyle \left\lfloor {\tfrac {n}{3}}\right\rfloor +\left\lfloor {\tfrac {n+2}{6}}\right\rfloor +\left\lfloor {\tfrac {n+4}{6}}\right\rfloor =\left\lfloor {\tfrac {n}{2}}\right\rfloor +\left\lfloor {\tfrac {n+3}{6}}\right\rfloor ,}$
2. ${\displaystyle \left\lfloor {\tfrac {1}{2}}+{\sqrt {n+{\tfrac {1}{2}}}}\right\rfloor =\left\lfloor {\tfrac {1}{2}}+{\sqrt {n+{\tfrac {1}{4}}}}\right\rfloor ,}$
3. ${\displaystyle \left\lfloor {\sqrt {n}}+{\sqrt {n+1}}\right\rfloor =\left\lfloor {\sqrt {4n+2}}\right\rfloor .}$

Probáronse tamén algunhas xeneralizacións das fórmulas anteriores. ^[7]

Problema sen resolver

O estudo do problema de Waring levou a un problema sen resolver:

Existe algún número enteiro positivo k ≥ 6 tal que ^[8]

${\displaystyle 3^{k}-2^{k}{\Bigl \lfloor }{\bigl (}{\tfrac {3}{2}}{\bigr )}^{k}{\Bigr \rfloor }>2^{k}-{\Bigl \lfloor }{\bigl (}{\tfrac {3}{2}}{\bigr )}^{k}{\Bigr \rfloor }-2\$ ?}

Mahler demostrou que só pode haber un número finito deses k. De momento non se coñece ningún.^[9]