Serie de Fourier
descomposición de funcións periódicas en sumas de formas sinusoidais máis sinxelas From Wikipedia, the free encyclopedia
Remove ads
En matemáticas, chámase serie de Fourier a unha forma de serie trigonométrica utilizada para representar funcións infinitas e periódicas complexas dos procesos físicos, na forma de funcións trigonométricas simples de senos e cosenos.[1] Isto resulta nunha simplificación da visualización e manipulación de funcións complexas. Foi creada en 1807 por Joseph Fourier (1768-1830).

A forma xeral da serie é:[2]
- onde e denomínanse coeficientes de Fourier da serie de Fourier da función y(x).
Fourier foi o primeiro que estudou tales series sistematicamente, aplicándoas á solución da ecuación da calor e publicando os seus resultados iniciais en 1807 e 1811. Esta área de investigación chámase algunhas veces Análise harmónica.
Remove ads
Definición
A serie de Fourier dunha función periódica de valores complexos , integrábel sobre o intervalo na recta real, defínese como unha serie trigonométrica da forma tal que os coeficientes de Fourier son números complexos definidos pola integral[3][4] A serie non converxe necesariamente (no sentido punto por punto) e, aínda que o faga, non é necesariamente igual a .
Só cando se cumpren certas condicións (por exemplo, se é continuamente diferenciábel) a serie de Fourier converxe a , é dicir,
O proceso de determinación dos coeficientes de Fourier dunha determinada función ou sinal chámase análise, mentres que a formación da serie trigonométrica asociada (ou as súas diversas aproximacións) chámase síntese.
Síntese
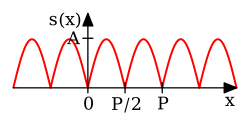
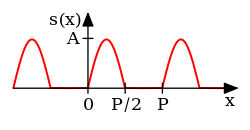
Unha serie de Fourier pódese escribir en varias formas equivalentes, mostradas aquí como sumas parciais da serie de Fourier de :[5]

Forma Seno-coseno
|
(Ec.1) |
Forma Exponencial
|
(Ec.2) |
Os harmónicos están indexados por un número enteiro, que tamén é o número de ciclos que realizan os sinusoides correspondentes no intervalo . Polo tanto, os sinusoides teñen :
- unha lonxitude de onda igual a nas mesmas unidades que .
- unha frecuencia igual a nas unidades recíprocas de .
Estas series poden representar funcións que son só unha suma dunha ou máis frecuencias no espectro harmónico (espectro que contién unicamente compoñentes de frecuencia cuxas frecuencias son múltiplos enteiros da frecuencia fundamental).
No límite , unha serie trigonométrica tamén pode representar as frecuencias intermedias e/ou funcións non sinusoidais debido ao número infinito de termos.
Análise
En xeral, os coeficientes están determinados pola análise dunha función dada cuxo dominio de definición é un intervalo de lonxitude .[a][6]
Coeficientes de Fourier
|
(Ec.3) |
O factor de escala dedúcese ao substituír a Ec.1 por Ec.3 e utilizar a ortogonalidade do sistema trigonométrico.[7]
A equivalencia da Ec.1 e a Ec.2 dedúcese da Fórmula de Euler resultando en:
Coeficientes da forma Exponencial
con sendo o valor medio de no intervalo .[8]
De xeito recíproco:
Relacións inversas
Exemplo


Considere unha función de dente de serra: Neste caso, os coeficientes de Fourier veñen dados por Pódese demostrar que a serie de Fourier converxe a en cada punto onde é diferenciábel, e polo tanto:
Cando , a serie de Fourier converxe a 0, que é a media do límite esquerdo e dereito de en . Este é un exemplo particular do Teorema de Dirichlet para as series de Fourier.
Este exemplo leva a unha solución do problema de Basilea.
Remove ads
Aplicacións
Enxeñaría
É común substituír a variábel x por ωt, resultando as compoñentes:
Polo tanto:
Remove ads
Táboa das series de Fourier comúns
Na seguinte táboa móstranse algúns pares comúns de funcións periódicas e os seus coeficientes da serie de Fourier.
- designa unha función periódica con período
- designan os coeficientes da serie de Fourier (forma seno-coseno) da función periódica
Remove ads
Táboa de regras básicas de transformación
- Véxase tamén: Transformada de Fourier#Propiedades básicas.
Esta táboa mostra algunhas operacións matemáticas no dominio do tempo e o efecto correspondente nos coeficientes da serie de Fourier. Notación:
- A conxugación complexa denotase cun asterisco.
- designan funcións periódicas ou funcións definidas só para
- designan os coeficientes da serie de Fourier (forma exponencial) de e
Remove ads
Propiedades
Relacións de simetría
Cando as partes reais e imaxinarias dunha función complexa se descompoñen nas súas partes pares e impares, hai catro compoñentes, indicados a continuación polos subíndices RE, RO, IE e IO. E hai unha correspondencia un a un entre as catro compoñentes complexas dunha función no tempo e das catro compoñentes complexas da súa transformanda en frecuencia:[11][12]
A partir diso, aparecen varias relacións, por exemplo :
- A transformada dunha función con valores reais é a dunción conxugada simétrica]] . E o recíproco tamén se cumpre.
- A transformada dunha función con valores imaxinarios é a función conxugada antisimétrica E o recíproco tamén se cumpre.
De forma similar interprétase o resto do diagrama.
Lema de Riemann-Lebesgue
- Artigo principal: Lema de Riemann-Lebesgue.
Se é integrábel, , e
Teorema de Parseval
- Artigo principal: Teorema de Parseval.
Se pertence a (periódica nun intervalo de lonxitude ), entón:
Teorema de Plancherel
- Artigo principal: Teorema de Plancherel.
Se son coeficientes e entón hai unha función única tal que para todo .
Teoremas de convolución
- Artigo principal: Teorema de convolución).
Dadas as funcións periódicas de período , e cos coeficientes da serie de Fourier e
- O produto punto por punto: tamén é -periódico, e os seus coeficientes da serie de Fourier veñen dados pola convolución discreta das secuencias e :
- A convolución periódica: tamén é -periódica, co coeficientes da serie de Fourier:
- Unha sucesión dobremente infinita en é a secuencia de coeficientes de Fourier dunha función en se é só se é unha convolución de dúas secuencias en . Ver [13]
Remove ads
Algunhas consecuencias positivas das propiedades de homomorfismo de exp
Debido a que as "funcións base" eikx son homomorfismos da liña real (máis concretamente, do "grupo do círculo") temos certas identidades útiles:
- Se daquela
- A transformada de Fourier é un morfismo: —isto é, a transformada de Fourier dunha convolución é o produto das transformadas de Fourier.
Remove ads
Formulación xeral
As útiles propiedades das series de Fourier son debidas principalmente á ortogonalidade e á propiedade de homomorfismo das funcións ei n x.
Outras sucesións de funcións ortogonais teñen propiedades similares, aínda que algunhas identidades útiles, concernendo por exemplo ás convolucións, non seguirán cumpríndose se se perde a "propiedade de homomorfismo".
Algúns exemplos son as secuencias de funcións de Bessel e os polinomios ortogonais. Tales sucesións obtéñense normalmente como solucións dunha ecuación diferencial; unha gran clase de tales sucesións útiles son solucións dos chamados problemas de Sturm-Liouville.
Remove ads
Notas
Véxase tamén
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads

![{\displaystyle y(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos(nx)+b_{n}\operatorname {sen} (nx)\right],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9132861b5517baf06b889f7a48c75fe59644acea)



![{\displaystyle [0,P]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e22a95e69fea5905acab328644408c110eedea0e)






















![{\displaystyle (-\pi ,\pi ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)


![{\displaystyle {\begin{aligned}s(x)&=a_{0}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}sin\left(nx\right)\right]\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {cando} \ (x-\pi )\ {\text{non é múltiplo de}}\ 2\pi .\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5a1e4e8ffb5d9859665654e901814295cf4c93e1)






 ...
...








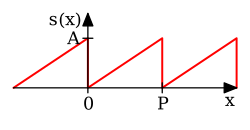








![{\displaystyle x\in [0,P].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)

 ,
,  ...
...

![{\displaystyle S[-n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i2\pi {\tfrac {x_{0}}{P}}n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7c56731e1382c8189ca81104cbade4d310fd72d8)


![{\displaystyle S[n-n_{0}]\!}](http://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)







![{\textstyle \lim _{|n|\to \infty }S[n]=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)



![{\displaystyle {\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx=\sum _{n=-\infty }\ {\Bigl |}S[n]{\Bigr |}^{2}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9e437dbd27c03153d522bccd7854e14c99d9b629)



![{\displaystyle S[n]=c_{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)



![{\displaystyle S[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle R[n],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)



![{\displaystyle H[n]=\{S*R\}[n].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)


![{\displaystyle L^{1}([0,2\pi ])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)



