Normális eloszlás

Az X valószínűségi változó normális eloszlást követ – vagy rövidebben: normális eloszlású – pontosan akkor, ha sűrűségfüggvénye

${\displaystyle f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\cdot e^{-{\frac {(x-m)^{2}}{2\sigma ^{2}}}},}$

A normális eloszlás sűrűségfüggvénye, ha

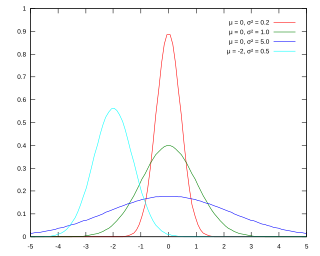
  m = 0 és σ² = 0,2

  m = 0 és σ² = 1 (standard normális eloszlás)

  m = 0 és σ² = 5

  m = –2 és σ² = 0,5

ahol a két paraméter, m és σ ∈ R, valamint σ > 0. A normális eloszlást szokták Gauss-eloszlásnak vagy néha normál eloszlásnak is nevezni.

Azt, hogy az X valószínűségi változó normális eloszlást követ, a következő módon szoktuk jelölni:

${\displaystyle X\sim {\mathcal {N}}(m,\sigma ^{2}).}$

Speciálisan, ha X ~ N(0, 1), akkor X-et standard normális eloszlásúnak (vagy sztenderd normális eloszlásúnak) nevezzük.

A fenti sűrűségfüggvény grafikonját alakja miatt szokás haranggörbének nevezni.

A normális eloszlást jellemző függvények

Eloszlásfüggvénye

${\displaystyle F(x)=\int \limits _{-\infty }^{x}{\frac {1}{\sigma {\sqrt {2\pi }}}}\cdot e^{-{\frac {(t-m)^{2}}{2\sigma ^{2}}}}dt\left(=\int \limits _{-\infty }^{x}f(t)dt\right)}$

Karakterisztikus függvénye

${\displaystyle \varphi (t)=e^{itm-{\frac {\sigma ^{2}t^{2}}{2}}}}$

Sűrűségfüggvényének tulajdonságai

• Maximumhelye m (de nem emiatt lesz az eloszlás várható értéke is m, az egybeesés a szimmetriának köszönhető).
• Szimmetrikus a maximumhelyére vonatkozóan.

• ${\displaystyle (\forall x\in \mathbb {R} )f(x)>0}$

• ${\displaystyle \lim _{x\to -\infty }f(x)=0}$

• ${\displaystyle \lim _{x\to \infty }f(x)=0}$

• ${\displaystyle \int _{-\infty }^{\infty }f(x)dx=1}$
• Folytonos függvény.

A normális eloszlást jellemző számok

Várható értéke

${\displaystyle \mathbf {E} (X)=m}$

Szórása

${\displaystyle \mathbf {D} (X)=\sigma }$

Momentumai

${\displaystyle \mathrm {E} \left(X^{p}\right)={\begin{cases}0&{\text{ha }}p{\text{ páratlan,}}\\\sigma ^{p}\,(p-1)!!&{\text{ha }}p{\text{ páros.}}\end{cases}}}$

Abszolút momentumai

${\displaystyle \operatorname {E} \left(|X|^{p}\right)=\sigma ^{p}\,(p-1)!!\cdot \left.{\begin{cases}{\sqrt {\frac {2}{\pi }}}&{\text{ha }}p{\text{ páratlan}}\\1&{\text{ha }}p{\text{ páros}}\end{cases}}\right\}=\sigma ^{p}\cdot {\frac {2^{\frac {p}{2}}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}}$

Ferdesége

${\displaystyle \beta _{1}(X)=0\,}$

Lapultsága

${\displaystyle \beta _{2}(X)=0\,}$

Normális eloszlású valószínűségi változó néhány fontosabb tulajdonsága

• Ha X ~ N(m, σ²), akkor bármilyen nullától különböző valós a és bármilyen valós b szám esetén az Y = aX + b valószínűségi változó is normális eloszlást követ, pontosabban Y ~ N(am + b, a²σ²).
  Az eloszlás eme tulajdonságán alapul a standardizálás módszere: ha X ~ N(m, σ²), akkor (X–m)/σ ~ N(0, 1).
• Normális eloszlású független valószínűségi változók összege is normális eloszlású. Pontosabban ha X₁ ~ N(m₁, σ₁²) és X₂ ~ N(m₂, σ₂²) független valószínűségi változók, akkor X₁ + X₂ ~ N(m₁ + m₂, σ₁² + σ₂²).

• Fordítva: ha X₁ és X₂ független valószínűségi változó, és X₁ + X₂ normális eloszlású, akkor X₁ is és X₂ is normális eloszlású.

Megjelenése máshol

1989-ben a Német Szövetségi Bank olyan 10 márkás bankjegyet bocsátott ki, melyen Gauss képe mellett a standard normális eloszlás sűrűségfüggvényének grafikonja és képlete is látható.^[1] Ez a bankjegy 2001-ig volt forgalomban, amikor is Németország áttért az euróra.