Arcotangente

In trigonometria l'arcotangente è definita come funzione inversa della restrizione della funzione tangente all'intervallo ${\displaystyle \left(-{\pi \over 2},{\pi \over 2}\right)\subset \mathbb {R} .}$^[1]

Il nome può esser fatto derivare dalla locuzione uno degli archi la cui tangente è la misura dell'angolo (infatti i radianti, unità di misurazione della funzione arcotangente, corrispondono al rapporto tra la lunghezza dell'arco di circonferenza individuato da un dato angolo e il raggio della circonferenza stessa). Con maggior precisione, si potrebbe affermare che l'arcotangente di ${\displaystyle x}$ è l'angolo di valore assoluto minore la cui tangente è ${\displaystyle x}$. È necessario considerare la restrizione della funzione tangente all'intervallo precedentemente indicato in modo da preservare l'invertibilità della funzione.

Notazione

La notazione matematica dell'arcotangente è ${\displaystyle \arctan }$ o ${\displaystyle {\rm {arctg}}}$; è comune anche la scrittura ${\displaystyle \tan ^{-1}}$. In diversi linguaggi di programmazione e sulle tastiere di alcune calcolatrici si utilizzano le forme ATAN e ATN.

Proprietà

Grafico della funzione y=arctan(x)

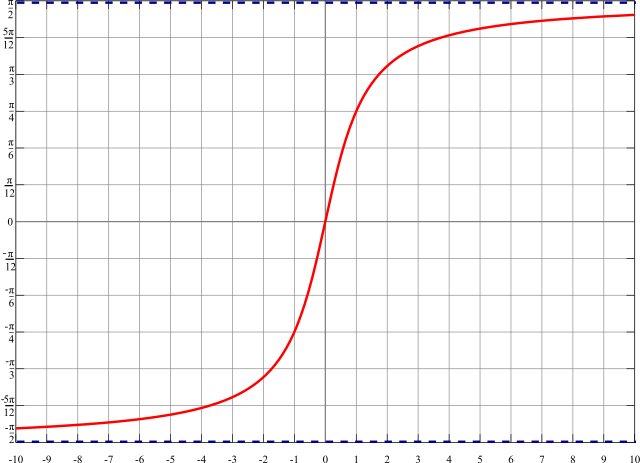
• L'arcotangente è una funzione definita sull'insieme dei numeri reali:^[2]

${\displaystyle \arctan$ :\mathbb {R} \rightarrow \left(-{\pi \over 2},{\pi \over 2}\right).}

• La sua immagine è l'intervallo:

${\displaystyle \arctan(\mathbb {R} )=\left(-{\pi \over 2},{\pi \over 2}\right)\subset \mathbb {R} .}$

• Ne esistono finiti i limiti agli estremi del dominio:

${\displaystyle \lim _{x\to -\infty }\arctan(x)=-{\pi \over 2},}$

${\displaystyle \lim _{x\to +\infty }\arctan(x)={\pi \over 2}.}$

• La funzione arcotangente è monotona strettamente crescente:

${\displaystyle \forall x_{1},x_{2}\in \mathbb {R} :x_{1}<x_{2}\Rightarrow \arctan(x_{1})<\arctan(x_{2}).}$

• È una funzione dispari (quindi il suo grafico è antisimmetrico):

${\displaystyle \arctan(x)=-\arctan(-x)\qquad {\text{o equivalentemente}}\qquad \arctan(-x)=-\arctan(x),}$

ed è di classe ${\displaystyle C^{\infty }}$ cioè è continua e ne esiste continua la derivata di ogni ordine:^[3]

${\displaystyle \forall \,x_{0}\in \mathbb {R} ,\forall n\in \mathbb {N} \quad \exists \;\lim _{x\to x_{0}}\arctan ^{(n)}(x)=\arctan ^{(n)}(x_{0})}$

${\displaystyle \arctan '(x)={1 \over 1+x^{2}},}$

${\displaystyle \arctan ''(x)={-2x \over \left(1+x^{2}\right)^{2}},}$

${\displaystyle \arctan ^{(3)}(x)={6x^{2}-2 \over \left(1+x^{2}\right)^{3}},}$

${\displaystyle \arctan ^{(4)}(x)={-24x^{3}+24x \over \left(1+x^{2}\right)^{4}},}$

${\displaystyle \cdots }$

La relativa serie di MacLaurin (ovvero serie di Taylor centrata nello zero) è:^[4]

${\displaystyle \arctan(x)=\sum _{k=0}^{\infty }(-1)^{k}{x^{2k+1} \over 2k+1}=x-{x^{3} \over 3}+{x^{5} \over 5}-{x^{7} \over 7}+\cdots }$

è una serie di Leibniz (quindi convergente) soltanto se ${\displaystyle \vert x\vert \leq 1.}$

È possibile combinare la somma o differenza di due arcotangenti in un'espressione dove l'arcotangente non figura più di una volta:

${\displaystyle \arctan \left(x_{1}\right)\pm \arctan \left(x_{2}\right)={\begin{cases}Y&\pm x_{1}x_{2}<1\\{\rm {segno}}\left(x_{1}\right)\,{\displaystyle \,\pi \; \over 2}\qquad &\pm x_{1}x_{2}=1\\Y+{\rm {segno}}\left(x_{1}\right)\,\pi &\pm x_{1}x_{2}>1\\\end{cases}}}$

nelle quali

${\displaystyle Y=\arctan \left({x_{1}\pm x_{2} \over 1\mp x_{1}x_{2}}\right).}$

Si ha inoltre che, per ${\displaystyle x>0}$:

${\displaystyle \arctan(x)+\arctan \left({1 \over x}\right)={\pi \over 2}.}$

Esistono vari modi per provare questa uguaglianza. Ad esempio, basta considerare un triangolo rettangolo avente i cateti di lunghezza ${\displaystyle x}$ e ${\displaystyle 1}$. L'angolo opposto al cateto di lunghezza ${\displaystyle x}$ avrà ampiezza pari a ${\displaystyle \arctan(x)}$, mentre l'angolo opposto al cateto di lunghezza ${\displaystyle 1}$ avrà ampiezza pari a ${\displaystyle \arctan \left({1 \over x}\right)}$. Per il teorema della somma degli angoli interni di un triangolo, vale quindi la relazione:

${\displaystyle \arctan(x)+\arctan \left({1 \over x}\right)+{\pi \over 2}=\pi ,}$

e quindi si giunge a:

${\displaystyle \arctan(x)+\arctan \left({1 \over x}\right)={\pi \over 2}.}$

Applicazioni

• In un triangolo rettangolo l'ampiezza in radianti di un angolo acuto equivale all'arcotangente del rapporto fra il suo cateto opposto e il cateto adiacente^[5].
• Grazie alle proprietà della funzione arcotangente, è possibile derivare formule e algoritmi molto efficienti per il calcolo delle cifre di pi greco. Queste formule sono conosciute come formule di tipo Machin.