Funzione di Weierstrass

In matematica, la funzione di Weierstraß è una funzione reale di variabile reale che ha la proprietà di essere continua in ogni punto, ma di non essere derivabile in nessuno. Deve il suo nome e la sua scoperta (nel 1872) a Karl Weierstraß.^[1]

Grafico della funzione di Weierstraß, con ingrandimento attorno ad un punto di minimo. Come si può notare nel cerchio, la funzione presenta auto similarità

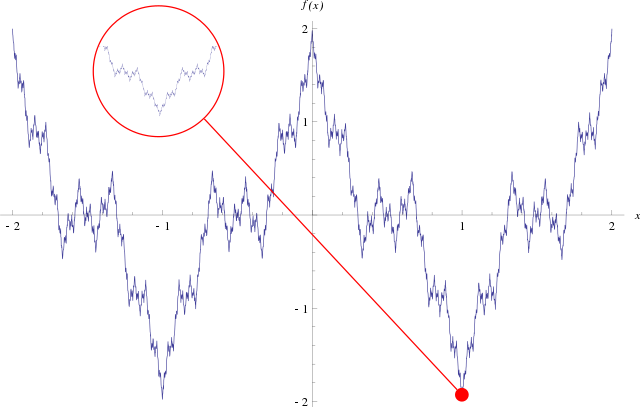
La funzione è un esempio ricorrente di funzione patologica, e storicamente si è trattato della prima funzione pubblicata in letteratura che corrisponde ad un controesempio all'affermazione che ogni funzione continua è derivabile a parte per un insieme di punti isolati del dominio.

Costruzione

La funzione è definita come:

${\displaystyle f(x)=\sum _{n=0}^{\infty }a^{n}\cos(b^{n}\pi x),}$

dove ${\displaystyle 0<a<1}$ e ${\displaystyle b}$ intero positivo dispari, tali che

${\displaystyle ab>1+{\frac {3}{2}}\pi .}$