Integrale di Fresnel

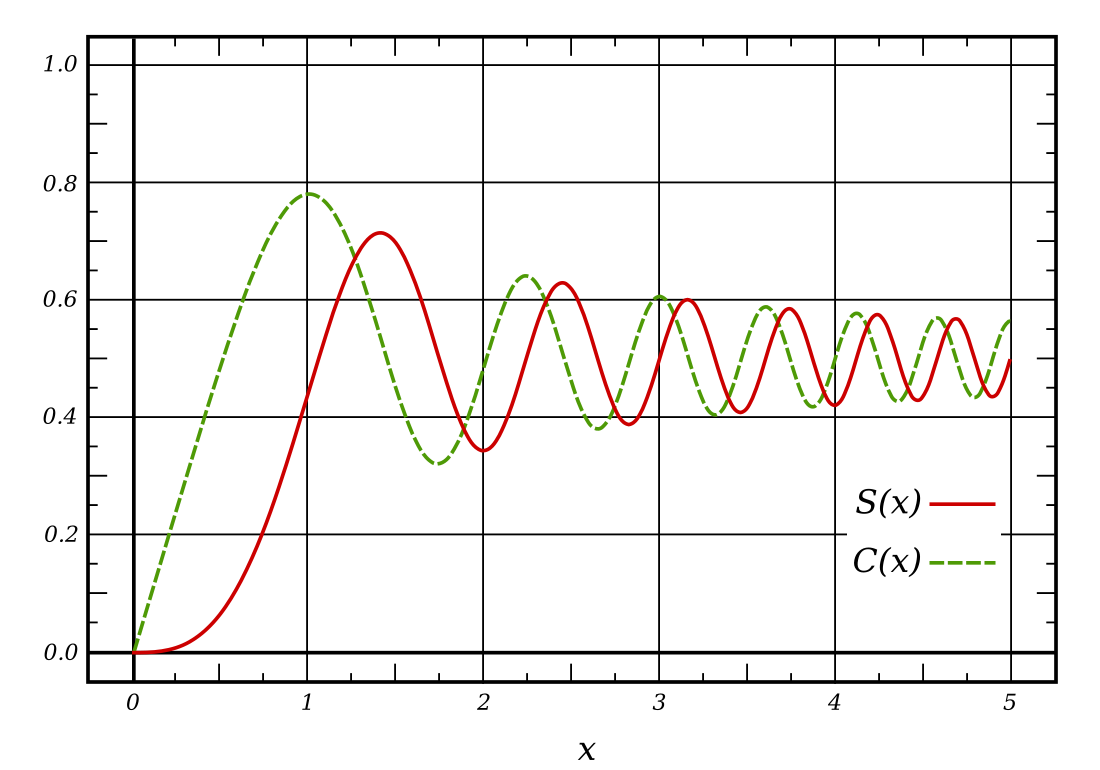
Gli integrali di Fresnel, ${\displaystyle S(x)}$ e ${\displaystyle C(x)}$, sono due funzioni speciali trascendenti introdotte in ottica dall'ingegnere francese Augustin-Jean Fresnel per studiare i fenomeni della diffrazione.

Grafico degli integrali di Fresnel normalizzati: ${\displaystyle S(x)=\int _{0}^{x}\sin \left({\frac {\pi }{2}}t^{2}\right)\,dt}$ e ${\displaystyle C(x)=\int _{0}^{x}\cos \left({\frac {\pi }{2}}t^{2}\right)\,dt}$.

Definizione

Esse sono definite attraverso le seguenti rappresentazioni:

Grafico degli stessi integrali non normalizzati: ${\displaystyle S(x)=\int _{0}^{x}\sin \left(t^{2}\right)\,dt}$ e ${\displaystyle C(x)=\int _{0}^{x}\cos \left(t^{2}\right)\,dt}$.

${\displaystyle S(x):=\int _{0}^{x}\sin \left({\frac {\pi }{2}}t^{2}\right)\,dt}$

${\displaystyle C(x):=\int _{0}^{x}\cos \left({\frac {\pi }{2}}t^{2}\right)\,dt}$

anche se altri autori preferiscono definirle senza il ${\displaystyle {\frac {\pi }{2}}}$ nell'argomento di seno e coseno.

Proprietà

• ${\displaystyle S(x)}$ e ${\displaystyle C(x)}$ sono funzioni dispari.
• ${\displaystyle C(iz)=iC(z)}$
• ${\displaystyle S(iz)=-iS(z)}$
• Gli integrali di Fresnel non possono essere calcolati in forma chiusa in termini di funzioni elementari, salvo casi particolari. Infatti essi convergono all'infinito e si ha:

  ${\displaystyle \lim _{x\to +\infty }S(x)=\lim _{x\to +\infty }C(x)={\frac {1}{2}}\,.}$

Dimostrazione limite per x tendente all'infinito

Poiché gli integrali di Fresnel non possono essere calcolati coi metodi tradizionali, una possibile dimostrazione di

${\displaystyle \int _{0}^{+\infty }\cos {(x^{2})}\,dx={\sqrt {\frac {\pi }{8}}}}$

sfrutta l'analisi complessa e il risultato dell'integrale di Gauss ${\displaystyle \int _{0}^{+\infty }e^{-x^{2}}dx={\frac {\sqrt {\pi }}{2}}}$. L'integrale di partenza può essere scritto come parte reale di un numero complesso secondo quella che è la forma polare di un numero complesso:

${\displaystyle \int _{0}^{+\infty }\cos {(x^{2})}\,dx=\Re {\left(\int _{0}^{+\infty }e^{ix^{2}}dx\right)}.}$

Curva semplice chiusa ${\displaystyle \gamma }$ nel piano complesso, suddivisa in ${\displaystyle \gamma _{1}}$, ${\displaystyle \gamma _{2}}$ e ${\displaystyle \gamma _{3}}$.

Per calcolare il secondo integrale si sfrutta il teorema di Cauchy-Goursat scegliendo come cammino chiuso di integrazione la curva chiusa ${\displaystyle \gamma }$ suddivisibile nei tre tratti ${\displaystyle \gamma _{1}}$, ${\displaystyle \gamma _{2}}$ e ${\displaystyle \gamma _{3}}$ come in figura:

${\displaystyle \oint _{\gamma }e^{iz^{2}}dz=\int _{\gamma _{1}}e^{iz^{2}}dz+\int _{\gamma _{2}}e^{iz^{2}}dz+\int _{\gamma _{3}}e^{iz^{2}}dz=0\,.}$

Questa operazione si può fare perché la funzione ${\displaystyle e^{iz^{2}}}$ è analitica in ${\displaystyle \mathbb {C} }$, che è semplicemente connesso.

Nel piano complesso ${\displaystyle \gamma _{3}}$ ha equazione ${\displaystyle z=re^{i\vartheta }}$, con ${\displaystyle r}$ variabile; per ricondursi all'integrale della gaussiana si impone che l'inclinazione di tale retta sia tale che ${\displaystyle iz^{2}=i{\left(re^{i\vartheta }\right)}^{2}=-r^{2}}$, ovvero ${\displaystyle \vartheta ={\frac {\pi }{4}}}$. Il terzo integrale diventa quindi

${\displaystyle \int _{\gamma _{3}}e^{iz^{2}}dz=\int _{R}^{0}e^{-r^{2}}e^{i{\frac {\pi }{4}}}\,dr\,,}$

che per ${\displaystyle x}$, ovvero ${\displaystyle R\rightarrow +\infty }$, vale

${\displaystyle \lim _{R\rightarrow +\infty }e^{i{\frac {\pi }{4}}}\int _{R}^{0}e^{-r^{2}}dr=-e^{i{\frac {\pi }{4}}}{\frac {\sqrt {\pi }}{2}}\,.}$

La curva ${\displaystyle \gamma _{2}}$ può essere parametrizzata come ${\displaystyle z=Re^{i\vartheta }}$, questa volta con ${\displaystyle \vartheta }$ variabile. Il secondo integrale diventa

${\displaystyle \int _{\gamma _{2}}e^{iz^{2}}dz=\int _{0}^{\frac {\pi }{4}}e^{iR^{2}e^{2i\vartheta }}(iR)\,e^{i\vartheta }\,d\vartheta =iR\int _{0}^{\frac {\pi }{4}}e^{iR^{2}\cos {(2\vartheta )}+i\vartheta }e^{-R^{2}\sin {(2\vartheta )}}\,d\vartheta \,.}$

Per ${\displaystyle 0\leq \vartheta \leq {\frac {\pi }{4}}}$, ${\displaystyle \sin {(2\vartheta )}\geq 0}$ e ${\displaystyle \cos {(2\vartheta )}\geq 0}$, e vale la disuguaglianza ${\displaystyle \sin {\vartheta }>{\frac {2}{\pi }}\vartheta }$. Ponendo ${\displaystyle 2\vartheta =\varphi }$, è possibile fare la seguente maggiorazione:

${\displaystyle 0\leq \left|{\frac {R}{2}}\int _{0}^{\frac {\pi }{2}}e^{iR^{2}\cos {\varphi }+i{\frac {\varphi }{2}}}e^{-R^{2}\sin {\varphi }}\,d\varphi \right|\leq {\frac {R}{2}}\int _{0}^{\frac {\pi }{2}}\left|e^{iR^{2}\cos {\varphi }+i{\frac {\varphi }{2}}}\right|\,\left|e^{-R^{2}\sin {\varphi }}\right|d\varphi ={\frac {R}{2}}\int _{0}^{\frac {\pi }{2}}e^{-R^{2}\sin {\varphi }}\,d\varphi \leq {\frac {R}{2}}\int _{0}^{\frac {\pi }{2}}e^{-R^{2}{\frac {2}{\pi }}\varphi }\,d\varphi =-{\frac {\pi }{4R}}\left(e^{-R^{2}}-1\right),}$

e dal teorema del confronto, segue che per ${\displaystyle R\rightarrow +\infty }$ il secondo integrale vale ${\displaystyle 0}$.

La curva ${\displaystyle \gamma _{1}}$, infine, può essere parametrizzata come ${\displaystyle z=x=R}$. Dal teorema di Cauchy-Goursat

${\displaystyle \int _{0}^{+\infty }e^{ix^{2}}dx=\int _{\gamma _{1}}e^{iz^{2}}dz=-\int _{\gamma _{3}}e^{iz^{2}}dz=e^{i{\frac {\pi }{4}}}{\frac {\sqrt {\pi }}{2}}\,.}$

L'integrale di Fresnel cercato diventa perciò

${\displaystyle \int _{0}^{+\infty }\cos {(x^{2})}\,dx=\Re {\left(\int _{0}^{+\infty }e^{ix^{2}}\,dx\right)}=\Re {\left(e^{i{\frac {\pi }{4}}}{\frac {\sqrt {\pi }}{2}}\right)}={\sqrt {\frac {\pi }{8}}}\,,}$

come volevasi dimostrare.

Relazione con altre funzioni speciali

${\displaystyle C(z)+iS(z)=zM\left({\frac {1}{2}},{\frac {3}{2}},i{\frac {\pi }{2}}z^{2}\right),}$

dove ${\displaystyle M}$ denota una funzione ipergeometrica confluente.

La relazione con la funzione degli errori è:

${\displaystyle C(z)+iS(z)={\frac {1+i}{2}}\mathrm {erf} \left[{\frac {\sqrt {\pi }}{2}}(1-i)z\right].}$

Bibliografia

• M. Abramowitz e I. Stegun Handbook of Mathematical Functions (Dover, New York, 1972) p. 300
• P. Drude Theory of Optics (Longmans, Green, and Co., New York, 1902) p. 188-203

Voci correlate

• Integrale di Gauss
• Integrale di Eulero

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su Integrale di Fresnel

Collegamenti esterni

• Integrale di Fresnel S(x) su functions.wolfram.com
• Integrale di Fresnel C(x) su functions.wolfram.com
• Integrali di Fresnel MathWorld

Controllo di autorità	GND (DE) 4155426-7

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica