Modulo di taglio

In meccanica dei solidi, il modulo di taglio, detto più propriamente modulo elastico tangenziale (altri nomi: modulo di scorrimento, di rigidità trasversale), è la costante di Lamé che esprime il rapporto sforzo-deformazione tangenziali.^[1]

Modulo di scorrimento o di taglio

La deformazione tangenziale

Il modulo di taglio viene considerato un parametro derivato, esprimibile in termini di due parametri elementari: il modulo elastico (normale, detto anche "modulo di Young") e il coefficiente di Poisson. In effetti, si può scegliere di caratterizzare un materiale secondo la modalità standard internazionale, con modulo elastico (normale) e modulo di Poisson, ma nulla vieta di scegliere di descriverlo invece col modulo tangenziale e il modulo di Poisson, o addirittura con modulo normale e tangenziale, lasciando quello di Poisson come implicito. La scelta standard è però la più diffusa, e porta solitamente a formule più semplici. Il modulo trasversale può essere normalmente calcolato a partire dagli altri due parametri attraverso:

${\displaystyle G={\frac {E}{2(1+\nu )}}}$

dove:

• ${\displaystyle \nu }$ è il rapporto di Poisson (o modulo di Poisson, secondo la denominazione)
• ${\displaystyle E}$ è il modulo elastico (normale, o modulo di Young, secondo la denominazione anglosassone)
• ${\displaystyle G}$ è il modulo elastico tangenziale (o modulo di taglio, secondo la vecchia denominazione)

Visualizzazione

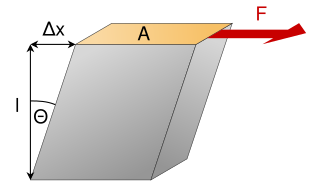
Data una piastra di lunghezza indefinita di spessore h, perpendicolare all'asse ${\displaystyle x}$, sulle cui facce agisce una coppia di tensioni tangenziali (o di taglio) di verso opposto ${\displaystyle T_{1}}$ e -${\displaystyle T_{1}}$, si produrrà uno spostamento ${\displaystyle \delta l/2}$ nel senso delle ${\displaystyle z}$ positive e ${\displaystyle \delta l/2}$ nel senso opposto. In pratica è come se una faccia rimanesse ferma e si producesse uno spostamento di ${\displaystyle \delta l}$.

Lo spostamento totale ${\displaystyle \delta }$l sarà in relazione allo sforzo di taglio ${\displaystyle T_{1}}$ e allo spessore ${\displaystyle h}$ secondo la relazione:

${\displaystyle dl={\frac {1}{\mu }}hT_{1}}$

dove ${\displaystyle \mu }$ è il modulo di taglio.

Considerando lo spostamento angolare ${\displaystyle \alpha }$, ponendo l'angolo uguale alla sua tangente, la relazione diventerà semplicemente:

${\displaystyle \alpha ={\frac {T_{1}}{\mu }}}$