ピタゴラスの定理

初等幾何学におけるピタゴラスの定理（ピタゴラスのていり、（英: Pythagorean theorem）は、直角三角形の3辺の長さの間に成り立つ関係について述べた定理である。その関係は、斜辺の長さを c, 他の2辺の長さを a, b とすると、

${\displaystyle c^{2}=a^{2}+b^{2}}$

ピタゴラスの定理

種類	定理
分野	ユークリッド幾何学
命題	2辺 (a, b) 上の2つの正方形の面積の和は、斜辺 (c) 上の正方形の面積に等しくなる。
数式	${\displaystyle a^{2}+b^{2}=c^{2}}$
一般化	余弦定理 空間幾何学 非ユークリッド幾何学 微分幾何学
結果	ピタゴラス数 逆ピタゴラスの定理 複素数 ユークリッド距離 ピタゴラスの三角恒等式

という等式の形で述べられる^[1][2][3]。

現在の日本では三平方の定理（さんへいほうのていり）とも呼ばれている。

ピタゴラスの定理によって、直角三角形において2辺の長さが分かっていれば、残りの1辺の長さを計算することができる^{[注 1]}。例えば、2次元直交座標系において、座標が分かっている2点間の距離を求めることができる。2点間の距離は、2点の各座標の差の 2乗の総和の平方根となる^{[注 2]}。このことは3次元直交座標系でも成り立つ。このようにして一般の有限次元直交座標系に対して導入される距離はユークリッド距離と呼ばれる。

(a, b, c) で特に全てが自然数であるものは、本質的に可算個あることが知られており、ピタゴラス数と呼ばれている。

定理の概要

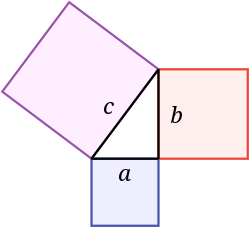
直角三角形において、斜辺の長さを c、直角をはさむ 2辺の長さをそれぞれ a, b とすると、次の等式が成り立ち、「ピタゴラスの定理」と呼ばれる：

${\displaystyle a^{2}+b^{2}=c^{2}}$

ここで a, b, c はいずれも正であるから、2辺の長さから残りの辺の長さを、次のように計算できる：

${\displaystyle a={\sqrt {c^{2}-b^{2}}}}$

${\displaystyle b={\sqrt {c^{2}-a^{2}}}}$

${\displaystyle c={\sqrt {a^{2}+b^{2}}}}$

この定理は、余弦定理によって一般の三角形に拡張される：任意の三角形において、1つの内角の大きさとそれをはさむ2辺の長さから残りの辺（対辺）の長さを計算できる。特にここで考えている内角の大きさが直角の場合、余弦定理はピタゴラスの等式に帰着する。

歴史

バビロニア数学について記された粘土板プリンプトン322

「ピタゴラスが直角二等辺三角形のタイルが敷き詰められた床を見ていて、この定理を思いついた」などいくつかの伝承が伝えられているが、実際はピタゴラスが生まれる前からピタゴラスの定理は広く知られていた。

判明している最初期のものは、ピタゴラスが生まれる1000年以上前のバビロン第1王朝時代ごろ（紀元前20世紀から16世紀の間）とされる^[4][5][6][7]。バビロニアの粘土板『プリンプトン322』には、ピタゴラスの定理に関わる要素が数多く含まれている。YBC 7289の裏面にはそれらしい記述がある。

古代エジプト数学にはピタゴラス数についての記述があり、ナイル川の氾濫のあとで土地を元どおり区割りする際に、直角を取るため 3:4:5の直角三角形が利用された可能性がある^[8]。紀元前2000年から1786年ごろに書かれた古代エジプトエジプト中王国のパピルス "Berlin Papyrus 6619（英語版）" には定理に関わる部分が欠けている。

紀元前3世紀に書かれた「ユークリッド原論」の中でピタゴラスの定理に該当するものは、第1巻の47番目の命題である。ここでは、昔から経験則として知られていたこの法則に、幾何学的な証明を与えている。しかし「原論」中ではピタゴラスについて何も言及がなく、この定理にも名前がついていない。

この定理がピタゴラス学派の業績であると述べる現存する最古の文献は、紀元5世紀のプロクロスによる『ユークリッド原論第一巻註解』である。同書の「第47番の命題」に関する記述は、定理の歴史的背景や、ピタゴラス派による研究について言及し、彼らがこの定理の証明をおこなったこと、さらに牡牛を生贄に捧げて祝ったと書く。後世においてこの定理をピタゴラスの業績とする根拠は、プロクロスの注解による^[9]。

インドの紀元前5-8世紀に書かれた『シュルバ・スートラ』などにも定理に関わる文章が見られる^[10]。しかし、これはバビロニア数学の影響を受けた結果ではないかという推測もされているが、結論には至っていない^[11]。

『周髀算経』におけるピタゴラスの定理の証明（中国語: 句股冪合以成弦冪）

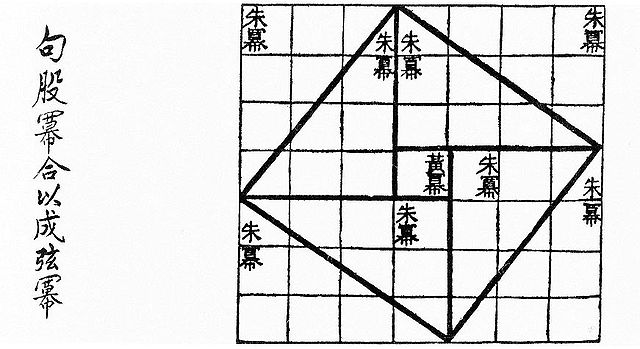
中国古代においては、『周髀算経』（紀元前2世紀前後）や『九章算術』の数学書でもこの定理が取り上げられている。中国ではこの定理を勾股定理、商高定理等と呼んで説明している。

レオナルド・ダ・ヴィンチによるピタゴラスの定理の証明。橙色の部分を 90度回転し、緑色の部分は裏返して図の位置にできる。

日本での呼称

日本の和算でも、中国での呼称を用いて鉤股弦の法（こうこげんのほう）等と呼んでいた^[12][13]。「勾（鈎）・股・弦」とはそれぞれ、a² + b² = c² (a < b < c) としたときの a, b, c を表している。

日本の明治時代の中等学校の教科書では「ピュタゴラスの定理」と呼ばれていた。

現在、ピタゴラスの定理は「三平方の定理」とも呼ばれているが、「三平方の定理」と呼ばれるようになったのは1942年（昭和17年）の太平洋戦争開始後のことである^[14]。

このときに「鉤股弦の定理」とする案などもあったが、末綱恕一（東大教授）の発案で「三平方の定理」に改められたとされる。

ピタゴラス数

→詳細は「ピタゴラス数」を参照

3辺の長さが何れも整数である直角三角形は、ピタゴラスの定理の項目の中で古くから知られた^[14]。例えば、紀元前1800年ごろのバビロニアの粘土板には、3辺の長さの表（例えば 4961² + 6480² = 8161² のようなもの）が出ている。

a² + b² = c² を満たす自然数の組 (a, b, c) をピタゴラス数 (Pythagorean triple) という。特に、a, b, c が互いに素であるピタゴラス数 (a, b, c) は原始ピタゴラス数 (primitive Pythagorean triple) と呼ばれる。全てのピタゴラス数は原始ピタゴラス数で (a, b, c) の正の整数倍 (ka, kb, kc) で表されるから、ピタゴラス数のリストを知るには、原始ピタゴラス数が本質的である。

ピタゴラス数 (a, b, c) が原始的であるためには、3つのうちある2つが互いに素であれば十分である。原始ピタゴラス数の小さい方のリストは、c < 100 で、a < b とすると次の通りである^[15]：

(a, b, c) = (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

ピタゴラス数の性質

→詳細は「ピタゴラス数」を参照

ピタゴラス数 (a, b, c) には、次の性質がある。

• a または b は 4 の倍数
• a または b は 3 の倍数
• a または b または c は 5 の倍数
  • したがって、積 abc は 60 の倍数である。

自然数の組 (a, b, c) が原始ピタゴラス数であるためには、ある自然数 m, n が

• m, n は互いに素
• m > n
• m と n の偶奇が異なる（一方が偶数で他方が奇数）

を満たすとして、

(a, b, c) = (m² − n², 2mn, m² + n²) または (2mn, m² − n², m² + n²)

であることが必要十分である^[16][17]。上記の (m, n) は無数に存在し重複がないので、原始ピタゴラス数は無数に存在し、すべての原始ピタゴラス数を重複なく列挙できる。

例えば

(m, n) = (2, 1) のとき (a, b, c) = (3, 4, 5)

(m, n) = (3, 2) のとき (a, b, c) = (5, 12, 13)

(m, n) = (4, 1) のとき (a, b, c) = (8, 15, 17)

である。a < b を満たす原始ピタゴラス数を a の昇順に並べた一覧表は以下のようになる^[18]。

原始ピタゴラス数の一覧表

# m n a b c 1 2 1 3 4 5 2 3 2 5 12 13 3 4 3 7 24 25 4 4 1 8 15 17 5 5 4 9 40 41 6 6 5 11 60 61 7 6 1 12 35 37 8 7 6 13 84 85 9 8 7 15 112 113 10 8 1 16 63 65 11 9 8 17 144 145 12 10 9 19 180 181 13 5 2 20 21 29 14 10 1 20 99 101 15 11 10 21 220 221 16 12 11 23 264 265 17 12 1 24 143 145 18 13 12 25 312 313 19 14 13 27 364 365 20 7 2 28 45 53 21 14 1 28 195 197 22 15 14 29 420 421 23 16 15 31 480 481 24 16 1 32 255 257 25 7 4 33 56 65

# m n a b c 26 17 16 33 544 545 27 18 17 35 612 613 28 9 2 36 77 85 29 18 1 36 323 325 30 19 18 37 684 685 31 8 5 39 80 89 32 20 19 39 760 761 33 20 1 40 399 401 34 21 20 41 840 841 35 22 21 43 924 925 36 11 2 44 117 125 37 22 1 44 483 485 38 23 22 45 1012 1013 39 24 23 47 1104 1105 40 8 3 48 55 73 41 24 1 48 575 577 42 25 24 49 1200 1201 43 10 7 51 140 149 44 26 25 51 1300 1301 45 13 2 52 165 173 46 26 1 52 675 677 47 27 26 53 1404 1405 48 28 27 55 1512 1513 49 28 1 56 783 785 50 11 8 57 176 185

# m n a b c 51 29 28 57 1624 1625 52 30 29 59 1740 1741 53 10 3 60 91 109 54 15 2 60 221 229 55 30 1 60 899 901 56 31 30 61 1860 1861 57 32 31 63 1984 1985 58 32 1 64 1023 1025 59 9 4 65 72 97 60 33 32 65 2112 2113 61 34 33 67 2244 2245 62 17 2 68 285 293 63 34 1 68 1155 1157 64 13 10 69 260 269 65 35 34 69 2380 2381 66 36 35 71 2520 2521 67 36 1 72 1295 1297 68 37 36 73 2664 2665 69 14 11 75 308 317 70 38 37 75 2812 2813 71 19 2 76 357 365 72 38 1 76 1443 1445 73 39 38 77 2964 2965 74 40 39 79 3120 3121 75 40 1 80 1599 1601

また、フランスの数学者ピエール・ド・フェルマーは一般のピタゴラス数 (a, b, c) に対して、S = 1/2ab（直角三角形の面積）は平方数でないことを無限降下法により証明した^[19]。

Jesmanowicz 予想

1956年に Jesmanowicz が次の予想を提出した：

(a, b, c) を原始ピタゴラス数、n を自然数とする。方程式：

${\displaystyle (an)^{x}+(bn)^{y}=(cn)^{z}}$

の自然数解 (x, y, z) は

${\displaystyle x=y=z=2}$

のみである。

特別なピタゴラス数

• 直角をはさむ2辺 a, b が連続する原始ピタゴラス数は

(3, 4, 5), (20, 21, 29), (119, 120, 169), …（オンライン整数列大辞典の数列 A114336）

である。この問題はフランスの数学者ピエール・ド・フェルマーが出題し、解も発見した^[20]。

• 斜辺 c と他の2辺の和 a + b が両方とも平方数になる最小のピタゴラス数は

a = 4565486027761, b = 1061652293520, c = 4687298610289

である。この問題はピエール・ド・フェルマーが出題し、解も発見した^[21]。

• ピタゴラス数 (a, b, c) において a, b の差が 1 で、c が平方数になるのは (119, 120, 169) に限られる^[22]。

119² + 120² = (13²)².

• 3辺の長さが a, b, c の直角三角形と、周の長さと面積の両方が同じ値となる、すべての辺の長さが整数である二等辺三角形が存在するならば、そのような直角三角形は全て相似であり、最小の (a, b, c) の値は、(135, 352, 377) である^[23]。

一般化

角の一般化

→詳細は「余弦定理」を参照

第二余弦定理

c² = a² + b² − 2ab cos C

はピタゴラスの定理を C = π/2 = 90° → cos C = 0 の場合として含む。 つまり、第二余弦定理はピタゴラスの定理を一般の三角形に対して拡張した定理になっている。

指数の一般化

→詳細は「フェルマーの最終定理」を参照

指数の 2 の部分を一般化すると

aⁿ + bⁿ = cⁿ

となる。n = 2 の場合、自明（つまり a, b, c の少なくとも1つが 0）や既知解（原始ピタゴラス数の定数倍）を除いても、整数解は実質無数に存在するが、n ≥ 3 の場合は非自明な整数解は存在しない。

次元の一般化

→詳細は「ド・グアの定理」を参照

3次元空間内に平面があるとき、その閉領域 S の面積は、yz 平面、zx 平面、xy 平面への射影の面積 S_x, S_y, S_z を用いて

${\displaystyle S^{2}={S_{x}}^{2}+{S_{y}}^{2}+{S_{z}}^{2}}$

と表される。これは高次元へ一般化できる。

ピタゴラスの定理の証明

この定理には数百通りもの異なる証明がある。

相似による証明

相似を用いた証明

頂点 C から斜辺 AB に下ろした垂線の足を H とする。△ABC と △ACH は相似である。ゆえに

${\displaystyle {\text{AC}}:{\text{AH}}={\text{AB}}:{\text{AC}}\Longrightarrow {\text{AH}}={{\text{AC}}\times {\text{AC}} \over {\text{AB}}}={b^{2} \over c}}$

であり、同様に

${\displaystyle {\text{BH}}={a^{2} \over c}}$

である。したがって

${\displaystyle c={\text{AH}}+{\text{BH}}={b^{2} \over c}+{a^{2} \over c}}$

であるから、両辺に c を掛けて

${\displaystyle c^{2}=a^{2}+b^{2}}$

を得る。

三角比による証明

前節の証明は、三角比を用いると簡単に表記できる：

${\displaystyle {\begin{aligned}c^{2}&=c\times c\\&=c\times ({\text{AH}}+{\text{BH}})\\&=c\times (b\cos A+a\cos B)\\&=b\times c\cos A+a\times c\cos B\\&=b\times b+a\times a\\&=a^{2}+b^{2}.\end{aligned}}}$

本証明を一般の三角形に拡張すると、第二余弦定理の証明が得られる。

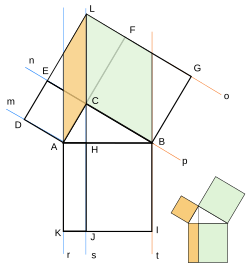
合同による証明^[24]

三平方の定理の合同による証明

${\displaystyle \bigtriangleup }$${\displaystyle ABC}$ と${\displaystyle \bigtriangleup }$ ${\displaystyle CDE}$ が合同になるように，図のように ${\displaystyle D}$ ,${\displaystyle E}$ を取る。

わかりやすいように整理すると、${\displaystyle a}$ が隣辺、${\displaystyle b}$ が対辺、${\displaystyle c}$ が斜辺の長さを示す。

四角形 ${\displaystyle ACBD}$ の面積 ${\displaystyle S}$ を二通りの方法で表す。

• ${\displaystyle AB}$ と ${\displaystyle CD}$ は直交するので， ${\displaystyle S={1 \over 2}AB\times CD={c^{2} \over 2}}$　

• ${\displaystyle \bigtriangleup }$ ${\displaystyle BCD}$ の面積は ${\displaystyle {a^{2} \over 2}}$，${\displaystyle \bigtriangleup }$${\displaystyle ACD}$ の面積は ${\displaystyle {b^{2} \over 2}}$ より ${\displaystyle S={1 \over 2}(a^{2}+b^{2})}$

よって、

${\displaystyle {c^{2} \over 2}={1 \over 2}(a^{2}+b^{2})}$

両辺に${\displaystyle 2}$をかけて

${\displaystyle c^{2}=a^{2}+b^{2}}$

以上2つの式より三平方の定理を得る。

外接円を用いた証明

外接円を用いた証明

∠C = 90° のとき、斜辺AB を直径とする円O を描くことができる。

このとき点C から直径AB に下ろした垂線の足を H とし、△CHO に対して三平方の定理を証明する。OA = OB = OC = c, CH = a, OH = b とする。

△AHC ∽ △BHC なので、

HA : HC = HC : HB

(OA − OH) : HC = HC : (OB + OH)

(c − b) : a = a : (c + b)

c² − b² = a²

∴ a² + b² = c² ◾️

正方形を用いた証明

正方形を用いた証明

△ABC と合同な4個の三角形を右図のように並べると、外側に一辺が a + b の正方形（以下「大正方形」）が、内側に一辺が c の正方形（以下「小正方形」）ができる。

（大正方形の面積）=（小正方形の面積）+（直角三角形の面積）× 4

である。大正方形の面積は (a + b)², 小正方形の面積は c², 直角三角形1個の面積は ${\displaystyle {\frac {1}{2}}ab}$ である。これらを代入すると、

${\displaystyle (a+b)^{2}=c^{2}+{\frac {1}{2}}ab\times 4}$

整理して

${\displaystyle a^{2}+b^{2}=c^{2}}$

を得る。

• 
  正方形を用いた証明の視覚化
• 
  正方形を用いた証明2
• 
  正方形を用いた証明3

内接円を用いた証明

△ABC において、内接円の半径 r を用いて面積 S を表すと

${\displaystyle S={\frac {1}{2}}r(a+b+c)}$

(1)

となるが、∠C = 90°より、

${\displaystyle S={\frac {1}{2}}ab}$

(2)

${\displaystyle r={\frac {1}{2}}(a+b-c)}$

(3)

となるから、(1) に (2), (3) を代入すると

${\displaystyle {\frac {1}{2}}ab={\frac {1}{4}}(a+b-c)(a+b+c)}$

整理すると

${\displaystyle a^{2}+b^{2}=c^{2}}$

が得られる。

オイラーの公式を用いた証明

三角関数と指数関数は冪級数によって定義されているものとする。（指数法則やオイラーの公式の証明に本定理が使用されない定義であればよい。）

[定義]

任意の0でない複素数 z に対し、z/|z|∈U だから

${\displaystyle {\begin{aligned}z&=|z|e^{i\theta }\\&=|z|(\cos \theta +i\sin \theta )\\\end{aligned}}}$

となる実数 θ が存在する。 このように絶対値 c := |z| と偏角 θ で表したものを z の「極表示」といい、 c を円の半径または、動径の長さもしくは、斜辺という。 このとき z = b + ai とすれば

${\displaystyle {\begin{aligned}a&=c\sin \theta \\b&=c\cos \theta \\\sin \theta &={\frac {a}{c}}\\\cos \theta &={\frac {b}{c}}\end{aligned}}}$

となる。 これが実変数 θ の関数としての cosθ, sinθ の幾何学的意味を表す。 即ちベクトル z の 虚軸、実軸への正射影が |z|sinθ, |z|cosθ なのである。 ここで、虚軸と実軸の交点は直交しているから、虚軸と実軸の正射影は直交する。

[証明]

まずsin² θ + cos² θ = 1 が任意の複素数 θ に対して成り立つことを（3通りの方法で）示す。

オイラーの公式より

${\displaystyle {\begin{aligned}1&=e^{0}=e^{i\theta -i\theta }=e^{i\theta }e^{-i\theta }\\&=(\cos \theta +i\sin \theta )(\cos \theta -i\sin \theta )\\&=\sin ^{2}\theta +\cos ^{2}\theta \end{aligned}}}$

または

${\displaystyle {\begin{aligned}\sin ^{2}\theta +\cos ^{2}\theta &=\left({\frac {e^{i\theta }-e^{-i\theta }}{2i}}\right)^{2}+\left({\frac {e^{i\theta }+e^{-i\theta }}{2}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }-2}{-4}}+{\frac {e^{2i\theta }+e^{-2i\theta }+2}{4}}\\&=1\end{aligned}}}$

もしくは、オイラーの公式から三角関数の半角の公式を導出する。

${\displaystyle {\begin{aligned}\sin ^{2}\theta &=\left({\frac {e^{i\theta }-e^{-i\theta }}{2i}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }-2}{-4}}\\&={\frac {1-\cos 2\theta }{2}}\ ,\\\cos ^{2}\theta &=\left({\frac {e^{i\theta }+e^{-i\theta }}{2}}\right)^{2}\\&={\frac {e^{2i\theta }+e^{-2i\theta }+2}{4}}\\&={\frac {1+\cos 2\theta }{2}}\ .\end{aligned}}}$

${\displaystyle \therefore \sin ^{2}\theta +\cos ^{2}\theta =1.}$^[25][26]

(1)

(1) の式はピタゴラスの基本三角関数公式 (Fundamental Pythagorean trigonometric identity) と呼ばれている^[27]。

(1) の時点ですでに単位円上において本定理の成立が明らかである。なぜならば、実数の範囲では、単位円上の偏角 θ の点の座標として定義した (cos θ, sin θ) と上記の冪級数による定義は一致するからである^[28]。

前提とした △ABC について、∠A = θ とおけば

${\displaystyle a=c\sin \theta }$

(2)

${\displaystyle b=c\cos \theta }$

(3)

(1), (2), (3) より

${\displaystyle {\begin{aligned}a^{2}+b^{2}&=(c\sin \theta )^{2}+(c\cos \theta )^{2}\\&=c^{2}(\sin ^{2}\theta +\cos ^{2}\theta )\\&=c^{2}\cdot 1=c^{2}\end{aligned}}}$

ゆえに

${\displaystyle a^{2}+b^{2}=c^{2}}$

が得られる。

三角関数の微分公式を用いた証明

正弦および余弦関数を微分すれば

${\displaystyle (\sin \theta )'=\cos \theta }$

(1)

${\displaystyle (\cos \theta )'=-\sin \theta }$

(2)

(1), (2) および微分公式より

${\displaystyle (\sin ^{2}\theta +\cos ^{2}\theta )'=2\sin \theta \cos \theta +2\cos \theta (-\sin \theta )=0}$

したがって

${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =C}$

ここで C は定数である。θ = 0 を代入すると sin 0 = 0, cos 0 = 1 であるので、C = 1 が得られる。よって

${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$

(3)

が得られる^[26]。

あとは前節と同様にして

${\displaystyle a^{2}+b^{2}=c^{2}}$

が得られる。

三角関数の不定積分を用いた証明

下記のように関数を定める。

${\displaystyle f(\theta )=\sin ^{2}\theta +\cos ^{2}\theta .}$

上記を漸化式を利用して不定積分すると

${\displaystyle {\begin{aligned}\int f(\theta )d\theta &=\int (\sin ^{2}\theta )d\theta +\int (\cos ^{2}\theta )d\theta \\&=\left({1 \over 2}\theta -{1 \over 2}\sin \theta \cos \theta +C_{1}\right)+\left({1 \over 2}\theta +{1 \over 2}\sin \theta \cos \theta +C_{2}\right)\\&=\theta +C\end{aligned}}}$

である^[29]。微分積分学の基本定理を考慮し、これを微分すると

${\displaystyle {\frac {d}{d\theta }}\int f(\theta )d\theta =f(\theta )={\frac {d}{d\theta }}(\theta +C)=1}$

である。したがって

${\displaystyle f(\theta )=\sin ^{2}\theta +\cos ^{2}\theta =1.}$

ゆえに、ピタゴラスの定理は成立する。

三角関数の加法定理を用いた証明

三角関数の加法定理は、三平方の定理を使わないで証明できる。本定理を使わないで証明した、三角関数の加法定理を使うと、

${\displaystyle {\begin{aligned}\cos ^{2}\theta +\sin ^{2}\theta &=\cos \theta \cos \theta +\sin \theta \sin \theta \\&=\cos(\theta -\theta )\\&=\cos 0=1\end{aligned}}}$

または

${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =\sin \theta \cos \left({\frac {\pi }{2}}-\theta \right)+\cos \theta \sin \left({\frac {\pi }{2}}-\theta \right)=\sin {\frac {\pi }{2}}=1}$

が得られる^[30][31]。 また、加法定理から導かれる半角公式を適用すると

${\displaystyle \sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}}$

${\displaystyle \cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}}$

したがって

${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$

が得られる。

あとはこれまでと同様にして

${\displaystyle a^{2}+b^{2}=c^{2}}$

が得られる^[30]。

冪級数展開を用いた証明

三角関数は級数によって定義されているものとし、cos θ と sin θ の自乗をそれぞれ計算すると

${\displaystyle {\begin{aligned}\sin ^{2}\theta &=\left\{\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}\theta ^{2n+1}\right\}^{2}\\&=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {(-1)^{k}}{(2k+1)!}}{\frac {(-1)^{n-k}}{(2n-2k+1)!}}\theta ^{2n+2}\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}\theta ^{2n+2}}{(2n+2)!}}\sum _{k=0}^{n}{\binom {2(n+1)}{2k+1}}\\&=\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}\\&=-\sum _{n=1}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}\\\cos ^{2}\theta &=\left\{\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}\theta ^{2n}\right\}^{2}\\&=\sum _{n=0}^{\infty }\sum _{k=0}^{n}{\frac {(-1)^{k}}{(2k)!}}{\frac {(-1)^{n-k}}{(2n-2k)!}}\theta ^{2n}\\&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n}{\binom {2n}{2k}}\\&=1+\sum _{n=1}^{\infty }{\frac {(-1)^{n}\theta ^{2n}}{(2n)!}}\sum _{k=0}^{n}{\binom {2n}{2k}}\end{aligned}}}$

となる^{[注 3]}。ここで二項定理より

${\displaystyle {\begin{aligned}\sum _{k=0}^{n}{\binom {2n}{2k}}-\sum _{k=0}^{n-1}{\binom {2n}{2k+1}}&=\sum _{m=0}^{2n}(-1)^{m}{2n \choose m}\\&=(1-1)^{2n}=0\end{aligned}}}$

である。したがって

${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$

が得られる。

あとはこれまでと同様にして

${\displaystyle a^{2}+b^{2}=c^{2}}$

が得られる^[32]。

回転行列を用いた証明

平面において原点を中心とする角 θ の回転の表現行列は

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}}$

であるが、このことも三平方の定理を用いないで証明が可能である。

R(θ) R (−θ) = I₂（単位行列）であるが^[33]、この式の左辺を直接計算すると

${\displaystyle {\begin{aligned}R(\theta )\cdot R(-\theta )&={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \end{bmatrix}}\\&={\begin{bmatrix}\cos ^{2}\theta +\sin ^{2}\theta &\cos \theta \sin \theta -\sin \theta \cos \theta \\\sin \theta \cos \theta -\cos \theta \sin \theta &\sin ^{2}\theta +\cos ^{2}\theta \end{bmatrix}}\\&={\begin{bmatrix}\sin ^{2}\theta +\cos ^{2}\theta &0\\0&\sin ^{2}\theta +\cos ^{2}\theta \end{bmatrix}}\end{aligned}}}$

となる^[34]。したがって

${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$

が得られる^[35]。

あとはこれまでと同様にして

${\displaystyle a^{2}+b^{2}=c^{2}}$

が得られる。

三角関数と双曲線関数を用いた証明

任意の z ∈ C に対し

${\displaystyle {\begin{aligned}\sin ^{2}iz+\cos ^{2}iz&=(i\sinh z)^{2}+\cosh ^{2}z\\&=\cosh ^{2}z-\sinh ^{2}z\\&=1\end{aligned}}}$

である^[36][37]。よって任意の θ ∈ C に対して

${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$

が成り立つ。

あとはこれまでと同様にして

${\displaystyle a^{2}+b^{2}=c^{2}}$

が得られる。

複素数の絶対値の定義を用いた証明

[定義]

複素数 z の絶対値 |z| は、複素数平面上において、原点 O(0) と P(z) の距離 OP に等しい。 複素数 z = b + ai（a, b は実数）（i は虚数単位）の絶対値はピタゴラスの定理とは関係なく次の式で定義される。

${\displaystyle |z|:={\sqrt {a^{2}+b^{2}}}}$

絶対値の定義より

${\displaystyle {\begin{aligned}|z|^{2}&=c^{2}\\&=a^{2}+b^{2}\\\end{aligned}}}$

である。

ピタゴラスの定理の逆

ピタゴラスの定理は、逆も真となる。すなわち、△ABC に対して

${\displaystyle a^{2}+b^{2}=c^{2}}$

が成立すれば、△ABC は ∠C = π/2 の直角三角形となる。

証明

ピタゴラスの定理に依存しない証明

ピタゴラスの定理に依存しない証明

△ABC が a² + b² = c² を満たすとする。線分 AB を b² : a² に内分する点を D とすると

${\displaystyle {\begin{aligned}{\text{AD}}&=c\times {\frac {b^{2}}{b^{2}+a^{2}}}\\&=c\times {\frac {b^{2}}{c^{2}}}\\&={\frac {b^{2}}{c}}\end{aligned}}}$

である。これより

${\displaystyle {\text{AC}}:{\text{AD}}=b:{\frac {b^{2}}{c}}=c:b={\text{AB}}:{\text{AC}}}$

であるから2辺比夾角相等より ${\displaystyle \triangle {\text{ACD}}\sim \triangle {\text{ABC}}}$。

${\displaystyle \therefore \angle {\text{ADC}}=\angle {\text{ACB}}}$

同様に

${\displaystyle \angle {\text{BDC}}=\angle {\text{BCA}}}$

となるから

${\displaystyle \angle {\text{ADC}}=\angle {\text{ACB}}=\angle {\text{BDC}}}$

(1)

となる。

(1) より

${\displaystyle \angle {\text{ADC}}=\angle {\text{BDC}}}$

(2)

一方

${\displaystyle \angle {\text{ADC}}+\angle {\text{BDC}}=\pi }$

(3)

であるから、(2), (3) より

${\displaystyle \angle {\text{ADC}}=\angle {\text{BDC}}={\frac {\pi }{2}}}$

(4)

(1), (4) より

${\displaystyle \angle {\text{ACB}}={\frac {\pi }{2}}}$

ゆえに △ABC は ∠C = π/2 の直角三角形である^[28]。

同一法を用いた証明

ピタゴラスの定理を用いた証明

B'C' = a, A'C' = b，∠C' = π/2 である直角三角形 A'B'C' において、A'B' = c' とすれば、ピタゴラスの定理より

${\displaystyle a^{2}+b^{2}=c'\,^{2}}$

(1)

が成り立つ。 一方、仮定から △ABC において

${\displaystyle a^{2}+b^{2}=c^{2}}$

(2)

が成り立っている。(1), (2) より

${\displaystyle c^{2}=c'\,^{2}}$

c > 0, c' > 0 より

${\displaystyle c=c'}$

したがって、3辺相等から

${\displaystyle \triangle {\text{ABC}}\equiv \triangle {\text{A}}'{\text{B}}'{\text{C}}'}$

∴ ∠C = ∠C' = π/2。ゆえに △ABC は ∠C = π/2 の直角三角形である^[28]。

対偶を用いた証明

△ABC において ∠C ≠ π/2 であると仮定する。頂点 A から直線 BC に下ろした垂線の足を D とし、AD = h, CD = d とする。

∠C < π/2 の場合、直角三角形 ABD においてピタゴラスの定理より

${\displaystyle {\begin{aligned}c^{2}&=(a-d)^{2}+h^{2}\\&=a^{2}-2ad+d^{2}+h^{2}\end{aligned}}}$

であり、同様に直角三角形 ACD では

${\displaystyle b^{2}=d^{2}+h^{2}}$

である。よって

${\displaystyle c^{2}=a^{2}-2ad+b^{2}<a^{2}+b^{2}}$

となる。

∠C > π/2 の場合も同様に考えて

${\displaystyle {\begin{aligned}c^{2}&=(a+d)^{2}+h^{2}\\&=a^{2}+2ad+d^{2}+h^{2}\\&=a^{2}+2ad+b^{2}\end{aligned}}}$

ゆえに

${\displaystyle c^{2}>a^{2}+b^{2}}$

となる。

よっていずれの場合も

${\displaystyle a^{2}+b^{2}\neq c^{2}}$

である。対偶を取って、a² + b² = c² ならば ∠C = π/2 である。

なお、この証明から分かるように、

• ∠C < π/2 ⇔ a² + b² > c²
• ∠C = π/2 ⇔ a² + b² = c²
• ∠C > π/2 ⇔ a² + b² < c²

という対応がある。

余弦定理を用いた証明

余弦定理を用いた証明

ピタゴラスの定理は既知とすると、それより導かれる余弦定理を用いることができる。△ABC において、a = BC, b = CA, c = AB, C = ∠ACB とおくと、余弦定理より

${\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C}$

一方、仮定より

${\displaystyle a^{2}+b^{2}=c^{2}}$

であるから

${\displaystyle \cos C=0}$

となる。三角形の内角の和は π であるから 0 < C < π より、

${\displaystyle C=\cos ^{-1}0={\frac {\pi }{2}}}$

ゆえに △ABC は ∠C = π/2 の直角三角形である。

ベクトルを用いた証明

△ABC において

${\displaystyle \Vert {\vec {c}}\|^{2}=\Vert {\vec {a}}\|^{2}+\Vert {\vec {b}}\|^{2}}$

であり

${\displaystyle {\vec {c}}={\vec {b}}-{\vec {a}}}$

である。 ここで

${\displaystyle {\begin{aligned}\Vert {\vec {c}}\|^{2}&={\vec {c}}\cdot {\vec {c}}\\&=({\vec {b}}-{\vec {a}})\cdot ({\vec {b}}-{\vec {a}})\\&=\Vert {\vec {b}}\|^{2}-2{\vec {b}}\cdot {\vec {a}}+\Vert {\vec {a}}\|^{2}\\\end{aligned}}}$

である。したがって

${\displaystyle {\vec {b}}\cdot {\vec {a}}=0}$

である。よって

${\displaystyle \angle {\text{C}}={\frac {\pi }{2}}}$

である。ゆえに、ピタゴラスの定理の逆が証明された。