ブレイド群

数学においてブレイド群（braid group、組みひも群とも呼ぶ）とは、直観的には平行に張られた複数の紐（braid）において、その隣り合う紐を交差させる操作を生成元とし、常に同じ絡まり方を生じる異なる交差操作の等式を関係式とする群である。特に紐がn本のときこの群をB_nと書く。

ブレイド群は1925年にエミール・アルティンにより初めて明確に定義された。しかしそれ以前に配置空間（英語版）の基本群として、1891年のアドルフ・フルヴィッツのモノドロミーの論文において暗に現れており^[1]、更に遡ってガウスもアルティンと同様の着想を得ていたとも考えられている。

定義

特殊なnの場合

以下n=4とする。

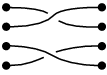
一列に並んだ4点が二組あり、それらの間を結ぶ平行な紐が4本ある下図（以下eにより参照）のような状況を考える。

${\displaystyle e}$

これらの紐に対し隣同士の紐を交差させる以下の3つの操作${\displaystyle \sigma _{1},\sigma _{2},\sigma _{3}}$を考える。

${\displaystyle \sigma _{1}}$

${\displaystyle \sigma _{2}}$

${\displaystyle \sigma _{3}}$

これらの紐の交差においては上下を区別しており、例えば以下は${\displaystyle \sigma _{1}}$とは異なる操作と看做される（これは後述の積の定義により${\displaystyle \sigma _{1}}$の逆元である${\displaystyle \sigma _{1}^{-1}}$と看做せる）。

${\displaystyle \sigma _{1},\sigma _{2},\sigma _{3}}$及び、その交差の上下を逆にした操作を繰り返して得られる一つの具体的な紐の状態をブレイド又は組紐と呼ぶ（以下上図の${\displaystyle \sigma _{1},\sigma _{2},\sigma _{3}}$自身もブレイドとも看做すこととする）。

二つのブレイドa, bがあるとき、aの右にbを繋げaの元の左の端点とbの右の端点を新たな端点とするブレイドを、aとbの積abと定義する。 以下に例を示す。

積の例

	a	b	ab
例1	${\displaystyle \sigma _{3}}$	${\displaystyle \sigma _{2}}$	${\displaystyle \sigma _{3}\sigma _{2}}$
例2	${\displaystyle \sigma _{1}^{-1}\sigma _{3}^{-1}}$	${\displaystyle \sigma _{1}\sigma _{3}^{-1}}$	${\displaystyle \sigma _{3}^{-2}}$

任意のブレイドと、冒頭のブレイド${\displaystyle e}$の積は元のブレイドを変えない（即ち${\displaystyle e}$は単位元）。 また任意のブレイドに対し、その右端の全点を通る縦線を軸として鏡映反転させたブレイドとの積を取ると${\displaystyle e}$となるため、常に逆元が存在することがわかる。 従ってブレイドは上記の積に関して群となり、この群が${\displaystyle B_{4}}$である。 定義より${\displaystyle B_{4}}$の任意のブレイドを${\displaystyle \sigma _{1},\sigma _{2},\sigma _{3}}$及び、その逆元の積として表現することができる。

${\displaystyle B_{4}}$を${\displaystyle \sigma _{1},\sigma _{2},\sigma _{3}}$を生成元とする群とみたとき、その基本関係式は下記1~3と定められる。これらは本質的に同じ絡まり方を表すブレイドに関する等式であり、1は対象に共通の紐がない交差操作は可換であることを示す条件で、2及び3はライデマイスター移動III型の同値性に相当する。

ライデマイスター移動III型

1. ${\displaystyle \sigma _{1}\sigma _{3}=\sigma _{3}\sigma _{1}}$
2. ${\displaystyle \sigma _{1}\sigma _{2}\sigma _{1}=\sigma _{2}\sigma _{1}\sigma _{2}}$
3. ${\displaystyle \sigma _{2}\sigma _{3}\sigma _{2}=\sigma _{3}\sigma _{2}\sigma _{3}}$

一般のnの場合

この例を n 本の紐へ一般化して、群 B_nは次の表示により定義される。^{[注 1]}

${\displaystyle B_{n}=\left\langle \sigma _{1},\ldots ,\sigma _{n-1}|\sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i},\sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1}\right\rangle \ .}$

ここに、最初の等式では|i − j| ≥ 2 であり、第二の等式では1 ≤ i ≤ n−2である。 ^{[注 2]} これらの関係式はブレイド関係式（braid relations）と呼ばれている。^{[注 3]}

基本的性質

• B₁ は自明な群、B₂ は無限巡回群 Z であり、B₃ は三葉結び目の結び目群と同型である。

• n ≥ 3 に対し、B_n は 2つの生成元を持つ自由群と同型な部分群を含む。従ってこれらの群は非可群な無限群である。

• 単位元を除くすべての B_n の元は、その位数が無限である。即ち、B_n は捩れを持たない。

• B_n 上には、Dehornoy順序（英語版）と呼ばれる左不変な全順序が存在する。

ブレイドの解釈

結び目としての解釈

→詳細は「組み紐 (数学)」を参照

ブレイドの両端をつなげることにより一つの結び目又は絡み目が得られる。 逆に、すべての結び目と絡み目は少なくとも一つのブレイドとして表現可能であることが知られている（アレクサンダーの定理）。 ブレイドは生成子 σ_iに関する語(word)として与えられるため、計算機プログラムで結び目を扱う方法として採用されている。

写像類群とブレイドの分類への関係

ブレイド群 B_n は、n 個の穴を有する円板の写像類群（英語版）(mapping class group)と同型であることを示すことができる。これは直感的には、写像類群の各元が穴同士を入れ替えるので、元の作用前後の同じ位置にある穴を繋ぐ紐の集合をブレイドと看做すことでブレイドと対応させることができることによる。

写像類群の元に関するニールセン・サーストン分類（英語版）(Nielsen-Thurston classification)によって、ブレイドを周期的、可約、擬アノソフの3種類に分類することができる。

ブレイド群の作用

置換による対称群の作用と類似して、様々な数学的設定におけるn個の対象の組やn重のテンソル積に対して、ブレイド群は以下の自然な作用を有する。

G を任意の群、X を G の元のすべての n個の組の集合で、それらの積が G の単位元となる集合とすると、${\displaystyle \sigma \in B_{n},\{x_{i}\}\in X}$に対する以下の写像はX の上へのB_nの作用である。

${\displaystyle \sigma _{i}\left(x_{1},\ldots ,x_{i-1},x_{i},x_{i+1},\ldots ,x_{n}\right)=\left(x_{1},\ldots ,x_{i-1},x_{i+1},x_{i+1}^{-1}x_{i}x_{i+1},x_{i+2},\ldots ,x_{n}\right).}$

この対応は、成分x_i と x_i+1 の位置を交換し、更にx_iをx_i+1に関する内部自己同型を付加しただけであるため、作用後の元の成分の積が再び単位元であることが保証される。また、これがブレイド群の関係式を満たすことも確認できる。

別な例として、ブレイド群の作用を持つモノイダル圏としてブレイドモノイダル圏（英語版）(braided monoidal category)が考えられている。そのような構造は、現代の数理物理学で重要な役目を果し、量子結び目不変量を導く。

ブレイド群の表現

ブレイド群 B_n の線形表現として古典的なBurau表現（英語版）や、Lawrence-Krammer(-Bigelow)表現（英語版）が知られている。^{[注 4]}

Burau表現は、1変数の整係数ローラン多項式環の一般線形群への表現と看做せる：

${\displaystyle B_{n}\to GL_{n-1}(\mathbb {Z} [\mathbb {Z} ]).}$

Burau表現が忠実であるか否かは長い間問題となっていたが、n ≥ 5 に対しては否定的であることが判明した。

Lawrence-Krammer(-Bigelow)表現は、2変数の整係数ローラン多項式環の一般線形群への表現と看做せる：

${\displaystyle B_{n}\to GL_{\binom {n}{2}}(\mathbb {Z} [\mathbb {Z} ^{2}]).}$

2001年頃Stephen BigelowとDaan Krammerが独立に、この表現を用いてすべてのブレイド群が線型であることを証明した。

1996年、C. Nayakとフランツ・ウィルチェック(Frank Wilczek)は、SO(3)の射影表現の類似として、ブレイド群の射影表現が分数量子ホール効果における準粒子に関する物理的意味を有することを提唱した^[2]。

その他

計算関係

ブレイドには生成元σ₁, ..., σ_nによる正規化表現が存在し、ブレイドの語の問題（英語版）(word problem)を効率的に処理することができる。 実際数式処理システムには、生成元で与えられたブレイドに対してこの問題を解くことができるものがある。^{[注 5]} 語の問題は、ローレンス・クラマー表現（英語版）(Lawrence-Krammer representation)を通しても効率的に解くことができる。

その他、ブレイド群に関する計算論的に難しい問題があるため、暗号理論への応用が提案されている。^[3]

B₃ とモジュラー群の関係

→詳細は「モジュラー群 § 群論的な性質」を参照

ブレイド群 B₃は、モジュラー群${\displaystyle \Gamma }$の中心拡大（central extension）である。即ち、${\displaystyle B_{3}}$の中心を${\displaystyle Z(B_{3})}$により表すとき以下の短完全列を満たす：

${\displaystyle 1\to Z(B_{3})\to B_{3}\to \Gamma \to 1}$

従って${\displaystyle \Gamma \cong B_{3}/Z(B_{3})}$である。

関連する群

純粋ブレイド群

ブレイドの紐の交差の上下を無視すると、n 本の紐のブレイドは n 個の元の置換を定める。実際ブレイド ${\displaystyle \sigma _{i}\in B_{n}}$の像を隣接互換 s_i = (i, i+1) ∈ S_n とする写像は、ブレイド群から対称群への全射群準同型 B_n → S_n である。 この準同型 B_n → S_n の核を純粋ブレイド群（pure braid group）と呼び、P_n と書く。即ち純粋ブレイド群は以下の短完全列を満たすものである。

${\displaystyle 1\to P_{n}\to B_{n}\to S_{n}\to 1.}$

純粋ブレイド群は、その元が単位置換に写像されるものであるため、幾何学的には各々の紐において起点と終点が必ず同じ位置にあるブレイドの全体と解釈することができる。

また純粋ブレイド群は、以下の分裂する短完全系列を満たすため、一般論から自由群の半直積を繰り返し取ったものと看做すこともできる。

${\displaystyle 1\to F_{n-1}\to P_{n}\to P_{n-1}\to 1.}$

関連事項

• 組みひも理論
• 非可換暗号理論（英語版）(Non-commutative cryptography）