ポンスレの閉形定理

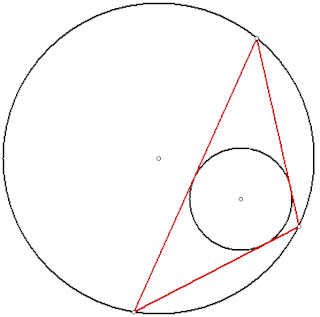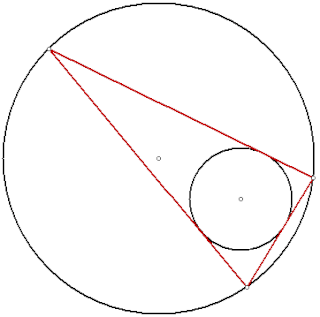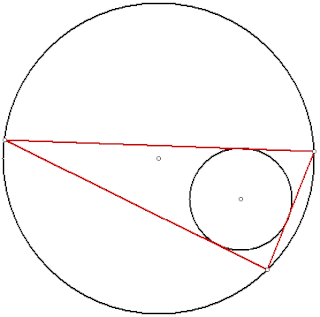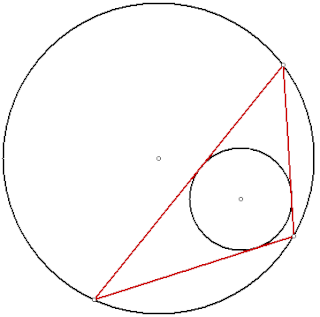
幾何学において、ポンスレの閉形定理（ポンスレのへいけいていり、英: Poncelet's closure theorem, Poncelet's porism）または単にポンスレの定理^[1][2]は、二つの円錐曲線にそれぞれ外接（英語版）、 内接する多角形が1つでも存在すれば、そのような多角形は無数に存在するという定理である^[3][4]。1746年、ウィリアム・チャップル が三角形の場合を証明し、1822年、ポンスレが一般の場合を解決した^[5][6][7]。

n = 3におけるポンスレの閉形定理。2円にそれぞれ内接、外接する三角形は無数にある。

主張

C,Dを二つの円錐曲線とする。3以上の整数nについて、あるn角形がCに外接する（多角形の頂点すべてがC上にある）かつDに内接する（多角形の辺すべてがDと接する）ならば、同様にCに外接しDに内接するn角形を無数に見つけることができる^[8]。CまたはD上の任意の点はそのような多角形の接点になり得る。

C,Dがともに円ならばこの多角形は双心多角形と呼ばれる。双心多角形は Poncelet's porism の一部である^{[9]:p. 94}。

証明の概要

C,Dを複素射影平面（英語版） P²上の曲線として見る。簡単のため、C, Dは単純な交点を持つとする（非特異で一般の位置（英語版）にある）。このときベズーの定理よりC, Dの交点は4つ存在する。点cを通るDの接線ℓ_dの接点をd、(c, d)をもつC × Dの部分代数多様体をXとする。c ∈ C ∩ Dならばdは1つ、でなければ2つ存在する。したがって、射影X → C ≃ P¹によりXは、4点以上で分岐した位数2の自己同型で表される。つまりXは楕円曲線である。 (c, d)を同一座標上の点(c, d' )へ移すXの対合を${\displaystyle \sigma }$とする。不動点をもつ楕円曲線の対合は、群として、x→p - xと表現されるので、${\displaystyle \sigma }$もこの形式となる。同様に射影X → Dも、C, Dの4つの共通接線とDの接点で分岐した位数2の自己同型であり、対合${\displaystyle \tau }$はx→q - xと一致する。したがって合成写像${\displaystyle \tau \sigma }$はXへの変換を表す。${\displaystyle \tau \sigma }$のべきが不動点を持つならば、そのべきはその不動点で恒等写像である必要がある。C, Dに言い換えると、（対応するdの存在する）ある点c ∈ Cが閉じた軌道をつくる（つまりn角形を作る）ならば、すべての点が不動であるということである。C, Dが退化した場合は極限を取ることで導かれる。

空間への拡張

1880年、フルヴィッツは次のように空間へ一般化した^[10][11]。

2つの空間三次曲線にそれぞれ内接・外接するような四面体が、2つでもあれば、そのような四面体は無数に存在する。

他に1901, 1904年にフォントネーに論じられ^[12][13]、1928年にフランツ・マイヤー（Franz Meyer）に双対を証明された、次のようなものもある^[14]。

与えられた空間三次曲線に内接し、二次曲面に外接する四面体は、一般に1つ存在し、2つ存在するならば、そのような四面体は無数に存在する。

フォントネーやブリカールは八面体や二十面体への拡張にも言及している^[15][16] 。