マクスウェルの定理 (幾何学)

幾何学における、マクスウェルの定理（マクスウェルのていり、英: Maxwell's theorem）は次の事柄を主張する定理である。

同じ印のついた線分は平行。

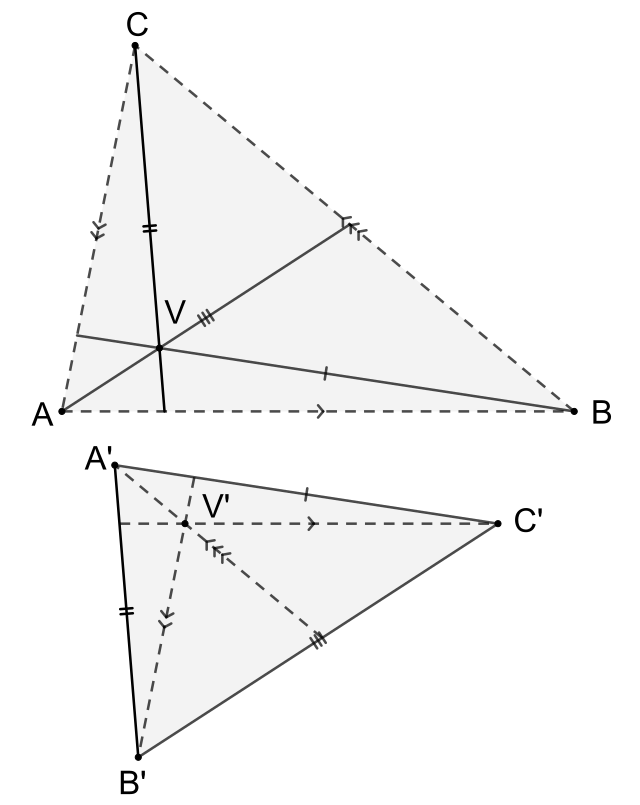
三角形${\displaystyle A'B'C'}$の辺と平行な、${\displaystyle ABC}$のチェバ線が一点で交わるとき、三角形${\displaystyle A'B'C'}$の辺と平行な、${\displaystyle ABC}$のチェバ線は一点で交わる。

三角形ABCとその辺上にない点Vについて、B'C',C'A',A'B'とそれぞれBC,CA,ABが平行になるような△A'B'C' を取る。このときそれぞれA',B',C'を通りB'C',C'A',A'B'に平行な直線は共点である。

この定理は物理学者であるジェームズ・クラーク・マクスウェルにちなんで名付けられた。

対平三角形

また、△ABC,△A'B'C' は対平^[1]（Parallelogic^[2][3]）であるという。

双対

マクスウェルの定理の双対は次の定理である^[4]。

△ABCの横断線がBC,CA,ABとA₁,B₁,C₁で交わり、別の三角形A'B'C'を、それぞれB'C',C'A',A'B'とAA₁,BB₁,CC₁が平行になるように作る。それぞれA',B',C'を通るBC,CA,ABに平行な直線とB'C',C'A',A'B'の交点をA₂,B₂,C₂とすれば、A₂,B₂,C₂は共線である。

関連項目

• 対垂
• チェバの定理
• メネラウスの定理