ミー・グリュナイゼンの状態方程式

ミー・グリュナイゼンの状態方程式（ミー・グリュナイゼンのじょうたいほうていしき、英: Mie–Grüneisen equation of state）は、固体の圧力と体積を特定の温度において関連付ける状態方程式である^[1][2]。この方程式は、衝撃により圧縮された固体内の圧力を決定するために使用される。ミー・グリュナイゼンの関係は、結晶格子の体積変化がその振動特性に与える影響を記述するグリュナイゼン定数モデルの特別な形式である。この状態方程式にはいくつかの種類が存在する。グリュナイゼンモデルは以下のように表せる。

${\displaystyle \Gamma =V\left({\frac {dp}{de}}\right)_{V}}$

ここで、${\displaystyle V}$およびは体積、${\displaystyle p}$は圧力、${\displaystyle e}$は内部エネルギー、Γは振動する原子群からの熱圧力を表すグリュナイゼン定数である。もしΓが${\displaystyle p}$および${\displaystyle e}$に依存しないと仮定する場合、グリュナイゼンモデルを積分して次の式を得ることができる。

${\displaystyle p-p_{0}={\frac {\Gamma }{V}}(e-e_{0})}$

ここで、${\displaystyle p_{0}}$および${\displaystyle e_{0}}$は参照状態での圧力および内部エネルギーで、通常は温度が0ケルビンである状態と仮定される。この場合、${\displaystyle p_{0}}$と${\displaystyle e_{0}}$は温度に依存せず、これらの値はランキン・ユゴニオの式に基づいて推定できる。ミー・グリュナイゼンの状態方程式は、この式の特別な形式として知られている。

歴史

グスタフ・ミー（英語版）は、1903年に高温における固体の状態方程式を導出するための分子間ポテンシャルを開発した^[3]。1912年には、エトヴァルト・グリュナイゼン（英語版）がミーのモデルを量子効果が重要になるデバイ模型以下の温度に拡張した^[4]。グリュナイゼンによる式の形式はより扱いやすく、ミー・グリュナイゼン状態方程式を導出する際の一般的な出発点として用いられる^[5]。

ミー・グリュナイゼンの状態方程式の式

計算力学で使用される温度補正された形式は以下の通りである^[6][7](p61)。

${\displaystyle p={\frac {\rho _{0}C_{0}^{2}\chi \left[1-{\frac {\Gamma _{0}}{2}}\,\chi \right]}{\left(1-s\chi \right)^{2}}}+\Gamma _{0}E;\quad \chi$ :=1-{\cfrac {\rho _{0}}{\rho }}}

ここで、${\displaystyle C_{0}}$は体積弾性波速度、${\displaystyle \rho _{0}}$は初期密度、${\displaystyle \rho }$は電流密度、${\displaystyle \Gamma _{0}}$は基準状態でのグリュナイゼン定数、${\displaystyle s=dU_{s}/dU_{p}}$は線形ユゴニオ傾斜係数、${\displaystyle U_{s}}$は衝撃波速度、${\displaystyle U_{p}}$は粒子速度、${\displaystyle E}$は単位基準体積あたりの内部エネルギーである。また、別の形式として以下が挙げられる。

${\displaystyle p={\frac {\rho _{0}C_{0}^{2}(\eta -1)\left[\eta -{\frac {\Gamma _{0}}{2}}(\eta -1)\right]}{\left[\eta -s(\eta -1)\right]^{2}}}+\Gamma _{0}E;\quad \eta$ :={\cfrac {\rho }{\rho _{0}}}\,}

内部エネルギーの概算は以下の式で計算できる。

${\displaystyle E={\frac {1}{V_{0}}}\int C_{v}dT\approx {\frac {C_{v}(T-T_{0})}{V_{0}}}=\rho _{0}c_{v}(T-T_{0})}$

ここで、${\displaystyle V_{0}}$は温度${\displaystyle T=T_{0}}$での基準体積、${\displaystyle C_{v}}$は熱容量（定積条件での熱容量）、${\displaystyle c_{v}}$は単位体積あたりの定積熱容量である。多くのシミュレーションでは、${\displaystyle C_{p}}$（定圧比熱）と${\displaystyle C_{v}}$が等しいと仮定される。

各種素材のパラメータ

材質	${\displaystyle \rho _{0}}$ (kg/m3)	${\displaystyle c_{v}}$ (J/kg-K)	${\displaystyle C_{0}}$ (m/s)	${\displaystyle s}$	${\displaystyle \Gamma _{0}}$ (${\displaystyle T<T_{1}}$)	${\displaystyle \Gamma _{0}}$ (${\displaystyle T>=T_{1}}$)	${\displaystyle T_{1}}$ (K)
銅	8960	390	3933 [8]	1.5 [8]	1.99 [9]	2.12 [9]	700

ミー・グリュナイゼンの状態方程式の導出

グリュナイゼンモデルから次のようになる。

${\displaystyle p-p_{0}={\frac {\Gamma }{V}}(e-e_{0})}$

(1)

${\displaystyle p_{0}}$および${\displaystyle e_{0}}$は基準状態での圧力と内部エネルギーを表す。質量、運動量、エネルギー保存のためのランキン・ユゴニオの式は、次のように表される。

${\displaystyle {\begin{aligned}\rho _{0}U_{s}&=\rho (U_{s}-U_{p})\,\\[1ex]p_{H}-p_{H0}&=\rho _{0}U_{s}U_{p}\,\\[1ex]p_{H}U_{p}&=\rho _{0}U_{s}\left({\frac {U_{p}^{2}}{2}}+E_{H}-E_{H0}\right)\end{aligned}}}$

ここで、${\displaystyle \rho _{0}}$は基準密度、${\displaystyle \rho }$は衝撃圧縮による密度、${\displaystyle p_{H}}$はユゴニオでの圧力、${\displaystyle E_{H}}$はユゴニオでの単位質量あたりの内部エネルギー、${\displaystyle U_{s}}$は衝撃速度、${\displaystyle U_{p}}$は粒子速度を表す。質量保存の法則から、次式が得られる。

${\displaystyle {\frac {U_{p}}{U_{s}}}=1-{\frac {\rho _{0}}{\rho }}=1-{\frac {V}{V_{0}}}=:\chi \,}$

ここで、${\displaystyle V=1/\rho }$を定義し、これは単位質量あたりの体積（比体積）を表す。多くの材料では、${\displaystyle U_{s}}$と${\displaystyle U_{p}}$は線形関係にあり、以下のように表される。

${\displaystyle 1=U_{s}=C_{0}+sU_{p}}$

ここで、${\displaystyle C_{0}}$と${\displaystyle s}$は材料に依存する。これにより、次式が得られる。

${\displaystyle U_{s}=C_{0}+s\chi U_{s}\quad }$

${\displaystyle \quad U_{s}={\frac {C_{0}}{1-s\chi }}\,}$

運動量の方程式は、（主にユゴニオでは、${\displaystyle p_{H}0=0}$とする。）次のようになる。

${\displaystyle p_{H}=\rho _{0}\chi U_{s}^{2}={\frac {\rho _{0}C_{0}^{2}\chi }{(1-s\chi )^{2}}}\,}$

同様に、エネルギー方程式は、次のようになる。

${\displaystyle p_{H}\chi U_{s}={\tfrac {1}{2}}\rho \chi ^{2}U_{s}^{3}+\rho _{0}U_{s}E_{H}={\tfrac {1}{2}}p_{H}\chi U_{s}+\rho _{0}U_{s}E_{H}\,}$

${\displaystyle e_{H}}$を解くと次のようになる。

${\displaystyle E_{H}={\tfrac {1}{2}}{\frac {p_{H}\chi }{\rho _{0}}}={\tfrac {1}{2}}p_{H}(V_{0}-V)}$

これらの${\displaystyle p_{H}}$と${\displaystyle E_{H}}$の式を用いると、ユゴニオでのグリュナイゼンモデルは次のようになる。

${\displaystyle p_{H}-p_{0}={\frac {\Gamma }{V}}\left({\frac {p_{H}\chi V_{0}}{2}}-e_{0}\right)\quad {\text{or}}\quad {\frac {\rho _{0}C_{0}^{2}\chi }{(1-s\chi )^{2}}}\left(1-{\frac {\chi }{2}}\,{\frac {\Gamma }{V}}\,V_{0}\right)-p_{0}=-{\frac {\Gamma }{V}}e_{0}\,}$

さらに、${\displaystyle 1=\Gamma /V=\Gamma _{0}/V_{0}}$と仮定し、${\displaystyle p_{0}=-de_{0}/dV}$とすると、次式が得られる。

${\displaystyle {\frac {\rho C_{0}^{2}\chi }{(1-s\chi )^{2}}}\left(1-{\frac {\Gamma _{0}\chi }{2}}\right)+{\frac {de_{0}}{dV}}+{\frac {\Gamma _{0}}{V_{0}}}e_{0}=0\,}$

(2)

上記の常微分方程式は、${\displaystyle V=V_{0}}$（${\displaystyle \chi =0}$）のとき、${\displaystyle e_{0}=0}$という初期条件を用いて解くことができる。正確な解は次の通りである。

${\displaystyle {\begin{aligned}e_{0}={\frac {\rho C_{0}^{2}V_{0}}{2s^{4}}}{\Biggl [}&\exp(\Gamma _{0}\chi )\left({\tfrac {\Gamma _{0}}{s}}-3\right)s^{2}-{\frac {\left[{\tfrac {\Gamma _{0}}{s}}-(3-s\chi )\right]s^{2}}{1-s\chi }}+\\&\exp \left[-{\tfrac {\Gamma _{0}}{s}}(1-s\chi )\right]\left(\Gamma _{0}^{2}-4\Gamma _{0}s+2s^{2}\right)\left({\text{Ei}}\left[{\tfrac {\Gamma _{0}}{s}}(1-s\chi )\right]-{\text{Ei}}\left[{\tfrac {\Gamma _{0}}{s}}\right]\right){\Biggr ]}\end{aligned}}}$

ここで、${\displaystyle Ei[z]}$は指数積分を表し、${\displaystyle p_{0}}$の式は次のようになる。

${\displaystyle {\begin{aligned}p_{0}=-{\frac {de_{0}}{dV}}={\frac {\rho C_{0}^{2}}{2s^{4}(1-\chi )}}{\Biggl [}&{\frac {s}{(1-s\chi )^{2}}}{\Bigl (}-\Gamma _{0}^{2}(1-\chi )(1-s\chi )+\Gamma _{0}[s\{4(\chi -1)\chi s-2\chi +3\}-1]\\&\qquad \qquad \quad -\exp(\Gamma _{0}\chi )[\Gamma _{0}(\chi -1)-1](1-s\chi )^{2}(\Gamma _{0}-3s)+s[3-\chi s\{(\chi -2)s+4\}]{\Bigr )}\\&-\exp \left[-{\tfrac {\Gamma _{0}}{s}}(1-s\chi )\right]\left[\Gamma _{0}(\chi -1)-1\right]\left(\Gamma _{0}^{2}-4\Gamma _{0}s+2s^{2}\right)\left({\text{Ei}}\left[{\tfrac {\Gamma _{0}}{s}}(1-s\chi )\right]-{\text{Ei}}\left[{\tfrac {\Gamma _{0}}{s}}\right]\right){\Biggr ]}\,\end{aligned}}}$

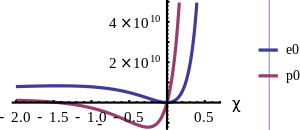
銅の${\displaystyle e_{0}}$および${\displaystyle p_{0}}$のプロットは、${\displaystyle \chi }$の関数として示される。

一般的な圧縮問題において、厳密解の近似として次のような冪級数解が使用される。

${\displaystyle e_{0}(V)=A+B\chi (V)+C\chi ^{2}(V)+D\chi ^{3}(V)+\cdots }$

${\displaystyle p_{0}(V)=-{\frac {de_{0}}{dV}}=-{\frac {de_{0}}{d\chi }}\,{\frac {d\chi }{dV}}={\frac {1}{V_{0}}}\,(B+2C\chi +3D\chi ^{2}+\cdots )\,}$

これをグリュナイゼンモデルに代入すると、次のようなミー・グリュナイゼンの状態方程式が得られる。

${\displaystyle p={\frac {1}{V_{0}}}\,(B+2C\chi +3D\chi ^{2}+\cdots )+{\frac {\Gamma _{0}}{V_{0}}}\left[e-(A+B\chi +C\chi ^{2}+D\chi ^{3}+\cdots )\right]\,}$

内部エネルギー${\displaystyle e_{0}}$が、${\displaystyle V=V_{0}}$（${\displaystyle \chi =0}$）のときに0であると仮定すると、${\displaystyle A=0}$となる。同様に、${\displaystyle p_{0}}$が${\displaystyle V=V_{0}}$のときに0であると仮定すると、${\displaystyle B=0}$となる。その結果、ミー・グリュナイゼンの状態方程式は次のように書き表せる。

${\displaystyle p={\frac {1}{V_{0}}}\left[2C\chi \left(1-{\tfrac {\Gamma _{0}}{2}}\chi \right)+3D\chi ^{2}\left(1-{\tfrac {\Gamma _{0}}{3}}\chi \right)+\cdots \right]+\Gamma _{0}E}$

ここで、${\displaystyle E}$は単位基準体積あたりの内部エネルギーを表す。この状態方程式にはいくつかの形式が存在する。

銅の厳密な状態方程式と、一次のミー・グリュナイゼンの状態方程式の比較。

一次項を方程式（2）に代入し、${\displaystyle C}$を解くと次のようになる。

${\displaystyle C={\frac {\rho _{0}C_{0}^{2}V_{0}}{2(1-s\chi )^{2}}}\,}$

これにより、${\displaystyle p}$の式は次のようになる。

${\displaystyle p={\frac {\rho _{0}C_{0}^{2}\chi }{(1-s\chi )^{2}}}\left(1-{\tfrac {\Gamma _{0}}{2}}\chi \right)+\Gamma _{0}E\,}$

これが、一般的に使用される一次のミー・グリュナイゼンの状態方程式である^[要出典]。