ルジャンドル変換

ルジャンドル変換（ルジャンドルへんかん、英: Legendre transformation）とは、凸解析において、関数の変数をその微分に変えるために用いられる変換である。このとき実数関数 f(x) は微分可能でなくてもよいが連続関数だとする^[1]。

名前はフランスの数学者、アドリアン＝マリ・ルジャンドルに因む。ルジャンドル変換は点と線の双対性、つまり凸な関数 y = f (x) は (x, y) の点の集合によって表現できるが、それらの傾きと切片の値で指定される接線の集合によっても等しく充分に表現できることに基いている。

凸関数をルジャンドル変換する際、変換前の関数が保持している情報は、変換後の関数においても完全に保たれる^[2]。解析力学においてはこの性質を利用して、ラグランジアンからルジャンドル変換によってハミルトニアンが得られる（⇒#解析力学）。物理学等において他にも広く応用されており、熱力学における熱力学関数間の変換などにも用いられる（⇒#熱力学）。

ルジャンドル変換をより一般化したものはルジャンドル＝フェンシェル変換と呼ばれる。

なお、与えられた関数をルジャンドル多項式やルジャンドル陪多項式を展開の基底関数に用いて、それら展開係数を求める変換のことも、ルジャンドル変換 (Legendre Transform) と呼ばれる。

定義

定義 (ルジャンドル変換) ― ${\displaystyle f~:~\mathbb {R} ^{n}\to \mathbb {R} \cup \{\pm \infty \}}$を関数とする。このとき、fのルジャンドル変換

${\displaystyle f^{*}~:~\mathbb {R} ^{n}\to \mathbb {R} \cup \{\pm \infty \}}$

は

${\displaystyle f^{*}(p):=\sup _{x\in \mathbb {R} ^{n}}\{\langle p,x\rangle -f(x)\}}$

により定義される^[3][4][5]。

ここで ${\displaystyle \langle \cdot ,\cdot \rangle }$は内積であり、supxは変数 x を動かしたときの上限を表す^{[注 1]}。 同じことだが下限を用いて

${\displaystyle f^{*}(p):=-\inf _{x\in \mathbb {R} ^{n}}\{f(x)-\langle p,x\rangle \}}$

とも表記できる。

ルジャンドル変換の直観的な意味は凸共役の項目を参照されたい。直観的な意味から、次が成立する事を示せる：

定理 (凸で滑らかな関数に対するルジャンドル変換の特徴づけ) ― fが凸でしかも滑らかであるとする。このとき、 ${\displaystyle x\in \mathbb {R} ^{n}}$を

${\displaystyle p=\nabla f(x)}$

が成立する点とすると、以下が成立する^[7]：

${\displaystyle f^{*}(p):=\langle p,x\rangle -f(x)}$

なお、${\displaystyle p=\nabla f(x)}$を満たすxが存在しない事もあり得ることに注意されたい^{[注 2]}。その場合、元の定義から${\displaystyle f^{*}(x)}$を求める必要がある。逆に${\displaystyle p=\nabla f(x)}$ を満たすxが一意に定まらず、複数存在することもあり得るが、その場合どのxを選んでも同じ${\displaystyle f^{*}(p)}$になる事がfの凸性から示せる。

関数 ${\displaystyle \scriptstyle f(x)}$ のルジャンドル変換 ${\displaystyle \scriptstyle f^{*}(p)=\sup _{x}\{px-f(x)\}}$（ただし ${\displaystyle \scriptstyle p={\dot {f}}(x)}$）は、${\displaystyle \scriptstyle x}$ における ${\displaystyle \scriptstyle f(x)}$ の接線の切片に対応している。

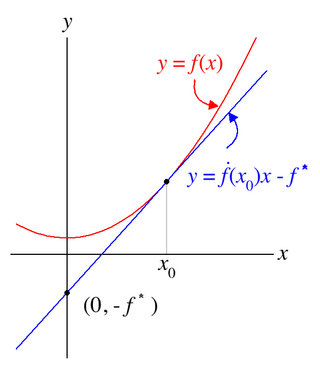
右図は上記の特徴づけを一次元の場合に直観的に説明したものである。${\displaystyle p\in \mathbb {R} }$に対し、

${\displaystyle p=f'(x_{0})}$

となる${\displaystyle x_{0}\in \mathbb {R} }$を取り、点x₀における${\displaystyle y=f(x)}$の接線

${\displaystyle y=f'(x_{0})x-f^{*}}$

を考えると、この接線が接点${\displaystyle (x_{0},f(x_{0}))}$を通る事から、

${\displaystyle f^{*}=f(x_{0})-f'(x_{0})x_{0}}$${\displaystyle =f(x_{0})-px_{0}}$${\displaystyle =f^{*}(p)}$

が従う。したがってルジャンドル変換は接線${\displaystyle y=f'(x_{0})x-f^{*}}$のy切片${\displaystyle -f^{*}}$にマイナスをつけたものである。

次にfが滑らかとは限らない場合のルジャンドル変換の振る舞いを見る。有限の値しか取らない凸関数fに対し、fは全点で連続であり^{[注 3]}、しかも任意の${\displaystyle d\in \mathbb {R} ^{n}}$に対しxにおけるd方向の（片側）方向微分

${\displaystyle \lim _{t\to +0}{f(x+td)-f(x) \over t}}$

が存在し、有現値である事が知られている^{[注 4]}（上式でtが正の方向から0に近づけていることに注意。負の方向から0に近づけたものとは値が異なることもあり得る^{[注 5]}）。

特に、（有限値しか取らない）凸関数fの定義域が１次元の場合は、左側方向微分${\displaystyle f'(x-0)}$と右側方向微分${\displaystyle f'(x+0)}$はいずれも存在して有限値である。これらを使って1次元のルジャンドル変換は以下のようにも特徴づけられる：

定理 (1次元の滑らかとは限らない凸関数に対するルジャンドル変換の特徴づけ) ― ${\displaystyle f~:~\mathbb {R} \to \mathbb {R} }$を（有限の値しか取らない）凸関数し、${\displaystyle p\in \mathbb {R} }$とする。このとき、${\displaystyle x\in \mathbb {R} ^{n}}$を

${\displaystyle f'(x-0)\leq p\leq f'(x+0)}$

を満たす値とすると、以下が成立する^[10]：

${\displaystyle f^{*}(x)=px-f(x)}$

前の定理と同様、そのようなxがそもそも存在しない場合もあるし、複数存在する場合にはどのxであっても${\displaystyle f^{*}(x)=px-f(x)}$は同じ値になる。

性質

二重共役

±∞を取らない凸関数は２回ルジャンドル変換を取るともとに戻る：

定理 ― （±∞を取らない）凸関数${\displaystyle f~:~\mathbb {R} ^{n}\to \mathbb {R} }$は${\displaystyle f^{**}=f}$を満たす^[11]。

なお${\displaystyle f}$が±∞を取る場合であっても、${\displaystyle f}$が恒等的に∞ではない場合、${\displaystyle x\in X}$において${\displaystyle f^{**}(x)=f(x)}$を満たす必要十分条件は、${\displaystyle f}$が${\displaystyle x}$において下半連続な事であることが示せる^[11]。凸関数は${\displaystyle \{x\in \mathbb {R} ^{n}\mid f(x)\neq \pm \infty \}}$の内点で連続であることが知られているので、下半連続性が問われるのは境界点だけである^[8]。

条件を満たさない場合、${\displaystyle f^{**}}$は${\displaystyle f}$に一致するとは限らない^[12]。条件を満たさない場合の詳細は凸共役の項目を参照されたい。

滑らかな関数に対する変換

また、f もそのルジャンドル変換 f ^* も2階微分可能なら、両者は逆数の関係にある^[13]。すなわち

$${\displaystyle f''(x)f^{*}{''}(p)=1\,.}$$

ただし x と p は p = f′(x) を満たすとする。

ヤングの不等式

以下の不等式が成り立つ。この種の不等式はヤングの不等式と呼ばれる。

$${\displaystyle f^{*}(p)+f(x)\geq px\,.}$$

ルジャンドル変換の定義より、

$${\displaystyle f^{*}(p)=\sup _{x}(px-f(x))\geq px-f(x)}$$

であるから、f(x) を両辺に足せば上述の不等式が成り立つ。

その他

• f (x) が下(上)に凸なら f ^*(p) も下(上)に凸。すなわちルジャンドル変換は凸性を保持する^[13]。
• f (x) の左微分と右微分が異なる（ f (x) が折れ線となる）点は、f ^*(p) が p に関して1次関数（直線）となる領域に対応する。逆に f (x) が x に関して直線となる領域は f ^*(p) が折れ線となる点に対応する^[14]。これは感覚的には、${\displaystyle f''(x)\to \infty }$ と ${\displaystyle f^{*}{''}(p)\to 0}$ が対応するとも解釈できる。
• 象徴的に書けば、以下のように x と p について対称な関係がある。

  ${\displaystyle p={\frac {\mathrm {d} f}{\mathrm {d} x}},\qquad x={\frac {\mathrm {d} f^{*}}{\mathrm {d} p}}}$

• f (x) の逆関数 f ^-1 (x) のルジャンドル変換は以下である（後述のヘルムホルツエネルギーとマシュー関数（英語版）の関係などに応用がある）。

  ${\displaystyle (f^{-1})^{*}(p)=-pf^{*}(1/p).}$

多変数関数

多変数関数に対しては、その一部の変数に関してだけのルジャンドル変換を考えることができる。

2変数関数 f(x, y) を x についてルジャンドル変換した関数を f^*(p, y) とする。このとき、変換されない変数 y はスペクテータと呼ばれる^[15]。スペクテータ y による偏微分はルジャンドル変換の影響を受けない。すなわち次式が成り立つ^[15]：

$${\displaystyle \left({\frac {\partial f(x,y)}{\partial y}}\right)_{x}=-\left({\frac {\partial f^{*}(p,y)}{\partial y}}\right)_{p}\,.}$$

応用例

熱力学

ルジャンドル変換で繋がっている熱力学関数とその変数のまとめ。

→「熱力学ポテンシャル」も参照

熱力学では、熱力学関数間の変換、すなわち内部エネルギー U(S, V) をエンタルピー H(S, p)、ヘルムホルツの自由エネルギー F(T, V) に、またそれらからギブスの自由エネルギー G(T, p) に変換する際にルジャンドル変換が用いられる。

$${\displaystyle {\begin{aligned}H(S,p)&=U(S,V)+pV,\\F(T,V)&=U(S,V)-TS,\\G(T,p)&=H(S,p)-TS\\&=F(T,V)+pV\\&=U(S,V)+pV-TS\,.\end{aligned}}}$$

ここで、V：体積、p：圧力、S：エントロピー、T：温度である。U が S, V について下に凸である^[16]ため、U(S, V), H(S, p), F(T, V), G(T, p) はルジャンドル変換を介して互いに等価である（同じ情報を持つ）。

ただしここではルジャンドル変換は

$${\displaystyle f^{\dagger }(p)=f(x)-xp\quad {\text{ at }}x{\text{ such that }}f'(x-0)\leq p\leq f'(x+0)}$$

という定義が用いられる^[17]。この定義でも上に述べた性質はほぼ同様に成り立つが、符号や凸性の変化などがある。たとえば逆変換は

$${\displaystyle f(x)=f^{\dagger }(p)+xp}$$

に変わるという不便さがある。しかし多変数関数をこの定義で変換した場合、凸性の上下については、変換した変数についてのみ逆転し残りの変数についてはもとのまま保持されるという簡便さがある。

熱力学では導関数の不連続性は相転移として現れる。

解析力学

→「シンプレクティック幾何学」も参照

解析力学におけるルジャンドル変換にThermodynamic square（英語版）を適用したときのオイラー＝ラグランジュ方程式。

Thermodynamic square（英語版）を適用したときの正準方程式。

解析力学では、ラグランジアン L をハミルトニアン H に変換する際に、ルジャンドル変換が用いられる。座標を q としたときに正準運動量を p = ∂L/∂·q として、ハミルトニアンは

$${\displaystyle H={\dot {q}}p-L}$$

と定義される^[18]。これによって、L(q, ·q) から H(q, p) になる。 実際これは以下の関係を満たす。

$${\displaystyle {\frac {\partial H}{\partial {\dot {q}}}}=p-{\frac {\partial L}{\partial {\dot {q}}}}=0\,.}$$

このハミルトニアンとオイラー＝ラグランジュ方程式あるいは最小作用の原理を組み合わせることで正準方程式が導かれる^[19]。 ハミルトニアンの全微分は、

$${\displaystyle \mathrm {d} H={\frac {\partial H}{\partial p}}\mathrm {d} p+{\frac {\partial H}{\partial q}}\mathrm {d} q+{\frac {\partial H}{\partial t}}\mathrm {d} t}$$

と書けるが、一方でハミルトニアンの定義より、

$${\displaystyle {\begin{aligned}\mathrm {d} H&=p\mathrm {d} {\dot {q}}+{\dot {q}}\mathrm {d} p-{\frac {\partial L}{\partial q}}\mathrm {d} q-{\frac {\partial L}{\partial {\dot {q}}}}\mathrm {d} {\dot {q}}-{\frac {\partial L}{\partial t}}\mathrm {d} t\\&=p\mathrm {d} {\dot {q}}+{\dot {q}}\mathrm {d} p-{\dot {p}}\mathrm {d} q-p\mathrm {d} {\dot {q}}-{\frac {\partial L}{\partial t}}\mathrm {d} t\\&={\dot {q}}\mathrm {d} p-{\dot {p}}\mathrm {d} q-{\frac {\partial L}{\partial t}}\mathrm {d} t\end{aligned}}}$$

となるので、ハミルトニアンの偏微分は以下の関係を満たす。この内、正準変数 p, q の偏微分に関する式をまとめて正準方程式 (canonical equations) と呼ぶ。

$${\displaystyle {\begin{cases}&{\dfrac {\partial H}{\partial p}}={\dot {q}}\\&{\dfrac {\partial H}{\partial q}}=-{\dot {p}}\\&{\dfrac {\mathrm {d} H}{\mathrm {d} t}}=-{\dfrac {\partial L}{\partial t}}\end{cases}}}$$

逆にハミルトニアンからラグランジアンを得る場合には、関数 L を以下のように定義し、

$${\displaystyle L={\dot {q}}p-H}$$

変数 p に対する偏微分が 0 になるようにする。すなわち、

$${\displaystyle {\frac {\partial L}{\partial p}}={\dot {q}}-{\frac {\partial H}{\partial p}}=0\,.}$$

結局このとき変数 ·q はハミルトニアンの運動量微分に等しくなる。

多変数の場合には、ラグランジアンのすべての一般化速度についてルジャンドル変換を施したものがハミルトニアンと呼ばれる。また部分的にルジャンドル変換をしたものはラウシアン（英語版） (Routhian) と呼ばれる^[20]。

正準変換

→「正準変換 § 母関数による構成」を参照

具体例

→「凸共役性 § 代表的な凸共役の表」も参照

滑らかな関数の例

最も簡単な例として特異性のない関数を挙げる^[21]。定数 s > 1 に対して

$${\displaystyle f(x)={\frac {\;x^{s}}{s}}\,,\quad x>0}$$

とする。この関数 f は下に凸かつ十分滑らかである。関数 f のルジャンドル変換 f^* は

$${\displaystyle f^{*}(p)={\frac {\;p^{t}}{t}}\,,\quad p>0}$$

となる。ただし t は 1/s + 1/t = 1 を満たす定数である。この例では f(x) と f ^*(p) は対称な形となる。特に s = t = 2 の場合、f(x) = x²/2 はルジャンドル変換で形を変えない。

導関数に定数となる領域がある例

f (x) がある区間で1次関数（直線）となる例を挙げる^[22]。

$${\displaystyle f(x)={\begin{cases}{\frac {x^{3}+x}{4}}&(0<x<1),\\x-{\frac {1}{2}}&(1\leq x<2),\\{\frac {x^{2}}{2}}-x+{\frac {3}{2}}&(2\leq x).\end{cases}}}$$

導関数 f'(x) が全領域で連続、かつ 1 < x < 2 で定数 f'(x) = 1 であることに注意する。この関数のルジャンドル変換は p = 1 で折れ線となり、

$${\displaystyle f^{*}(p)={\begin{cases}{\frac {1}{2}}\left({\frac {4p-1}{3}}\right)^{3/2}&({\frac {1}{4}}<p<1),\\{\frac {1}{2}}(p^{2}+2p-2)&(1\leq p)\end{cases}}}$$

となる。

斉次関数

f(x) が k 次の斉次関数であるなら、そのルジャンドル変換は

$${\displaystyle {\frac {\partial f}{\partial x}}x-f=(k-1)f}$$

である^[23]。特に k = 1 のとき、f(x) のルジャンドル変換は 0 となる。

注釈

1. ルジャンドル変換を

   $${\displaystyle f^{*}(p)=\max _{x}(px-f(x))}$$

   または

   $${\displaystyle f^{*}(p)=-\min _{x}(f(x)-px)}$$

   としている文献もあるが^[6]、この場合最大値や最小値の存在を暗に仮定している。 しかし例えば${\displaystyle f(x)=e^{-x}}$は${\displaystyle f^{*}(0)=0}$を達成する${\displaystyle x\in \mathbb {R} }$は存在しない。
2. 例えば、${\displaystyle f(x)=\mathrm {e} ^{-x}}$ や${\displaystyle g(x)={\begin{cases}{1 \over x}&{\text{if }}x>0\\\infty &{\text{otherwise}}\end{cases}}}$ は凸でしかも滑らかであるが、${\displaystyle p\geq 0}$に対しては${\displaystyle p=f'(x)}$、${\displaystyle p=g'(x)}$となる${\displaystyle x\in \mathbb {R} }$は存在しない。
3. より一般に（∞も取りうる）凸関数fに対し${\displaystyle \mathrm {dom} f=\{x\in \mathbb {R} ^{n}\mid f(x)\neq \pm \infty \}}$とすると、${\displaystyle \mathrm {dom} f}$の内点xでfは連続である^[8]。
   なお、「${\displaystyle \mathrm {dom} f}$の内点」という条件は必須である。例えば ${\displaystyle f(x)={\begin{cases}x^{2}&{\text{if }}x\geq 0\\\infty &{\text{otherwise}}\end{cases}}}$ は原点${\displaystyle x=0}$において連続ではないし、左側方向微分も存在しない。
4. より一般に、${\displaystyle x\in \mathrm {core} (\mathrm {dom} f)}$における任意の方向の片側方向微分が存在する^[9]。${\displaystyle \mathrm {core} }$の定義は凸共役の項目を参照されたい。
5. 例えば${\displaystyle y=|x|}$の${\displaystyle x=0}$における方向微分。