トップQs
タイムライン
チャット
視点
代数螺旋
ウィキメディアの一覧記事 ウィキペディアから
Remove ads
代数螺旋(だいすうらせん)は、代数的な式によって表される螺旋である。アルキメデスの螺旋、放物螺旋、双曲螺旋、リチュースなどがある。対数螺旋は代数螺旋には含まれない。
アルキメデスの螺旋
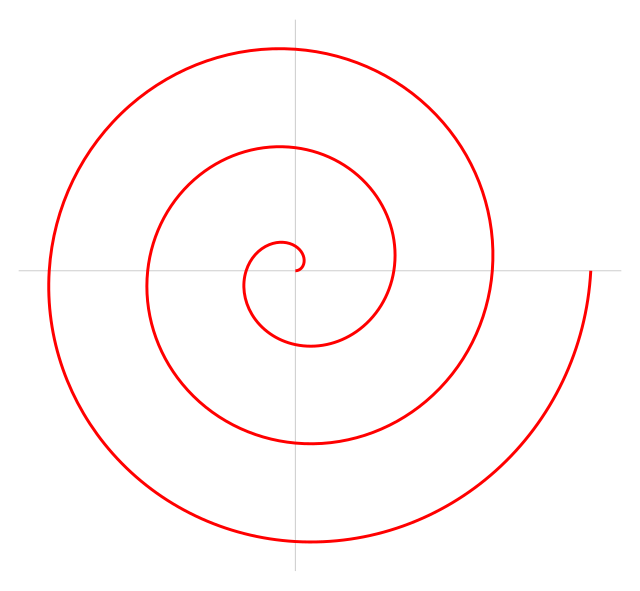
→詳細は「アルキメデスの螺旋」を参照
アルキメデスの螺旋(-らせん Archimedes' spiral)は極座標の方程式 によって表される曲線で、線同士の間隔が等しい渦巻である。 が負の場合も含めると、y 軸に対して線対称となる。アルキメデス螺旋とも。
放物螺旋

→詳細は「フェルマー螺旋」を参照
放物螺旋(ほうぶつらせん、Parabolic Spiral)は極座標の方程式 によって表される曲線である。渦は外側にいくほど( が大きくなるほど)間隔が狭くなっていく。
双曲螺旋

→詳細は「双曲螺旋」を参照
双曲螺旋(そうきょくらせん hyperbolic spiral)は極座標の方程式 によって表される曲線である[1]。
パラメータ表示では と表される。
y = a を漸近線に持つ。
が負の場合も含めると、y 軸に対して線対称となる。
リチュース

→詳細は「リチュース (数学)」を参照
リチュース(Lituus)は によって表される曲線である[1]。
が大きくなるにつれて、渦を巻いて原点()に近づいていく。
Remove ads
関連項目
出典
外部リンク
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads






