トップQs
タイムライン
チャット
視点
名称のあるグラフのギャラリー
ウィキペディアから
Remove ads
特徴的なグラフ
- バラバン10-ケージ
- バラバン11-ケージ
- ビディアキキューブ
- ブリンクマングラフ
- ブルグラフ
- バタフライグラフ
- フバータルグラフ
- ダイアモンドグラフ
- デューラーグラフ
- Ellingham–Horton 54-graph
- Ellingham–Horton 78-graph
- Errera graph
- フランクリングラフ
- フルフトグラフ
- Goldner–Harary graph
- Grötzsch graph
- Harries graph
- Harries–Wong graph
- Herschel graph
- ホフマングラフ
- Holt graph
- Horton graph
- Kittell graph
- Markström graph
- McGee graph
- Meredith graph
- Moser spindle
- Sousselier graph
- Poussin graph
- Robertson graph
- Young–Fibonacci graph
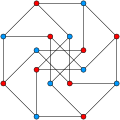
- Wagner graph
- Wiener–Araya graph
Remove ads
Highly symmetric graphs
強正則グラフ
→「強正則グラフ」も参照
- Clebsch graph
- Hall–Janko graph
- Hoffman–Singleton graph
- Higman–Sims graph
- Paley graph of order 13
- Shrikhande graph
- Schläfli graph
- Brouwer–Haemers graph
- Local McLaughlin graph
- Perkel graph
- Gewirtz graph
対称グラフ
→「対称グラフ」も参照
- メビウス-カントールグラフ
- パップスグラフ
- デザルググラフ
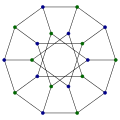
- ナウルグラフ
- コクセターグラフ
- トゥッテ-コクセターグラフ
- ディックグラフ
- Klein graph
- フォスターグラフ
- ビッグス-スミスグラフ
- The ラドグラフ
半対称グラフ
- グレイグラフ
- リュブリャナグラフ
- トゥッテ12-ケージ
Remove ads
Graph families
要約
視点
完全グラフ
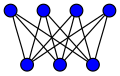
完全2部グラフ
→「完全2部グラフ」も参照
- , the utility graph
閉路グラフ
個の頂点を持つ閉路グラフはn-cycleと呼ばれで表される。
フレンドシップグラフ
フレンドシップグラフはn個の 閉路グラフC3 を一つの頂点で繋いで構成する。[2]

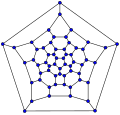
フラーレングラフ
グラフ理論においてフラーレンとは、3-正則平面グラフであって無限面を含めて全ての面が五角形または六角形であるもの。オイラーの多面体公式 V – E + F = 2(V, E, F はそれぞれ頂点数、辺数、面数)から、フラーレンにはちょうど12個の五角形と V/2–10 個の六角形がある。フラーレングラフは対応するフラーレン化合物のシュレーゲル図である。
- 20-fullerene (dodecahedral graph)
- 24-fullerene (Hexagonal truncated trapezohedron graph)
- 26-fullerene
- 60-fullerene (truncated icosahedral graph)
- 70-fullerene
同じ六角形の面の数で同型でないフラーレンを作るアルゴリズムがG. BrinkmannとA. Dressによって発表された。[3]
正多面体
4つの頂点の完全グラフは正四面体の骨格を形作る。このように超立方体グラフは正多面体の骨格を表している。
Truncated solids
- Truncated tetrahedron
- Truncated cube
- Truncated octahedron
- Truncated dodecahedron
- Truncated icosahedron
スナーク
スナーク はブリッジを持たない立方体グラフのうち辺彩色に4色必要なものの総称である。最も小さいスナークグラフはピーターセングラフである。
- Blanuša snark (first)
- Blanuša snark (second)
- Double-star snark
- Flower snark
- Loupekine snark (first)
- Loupekine snark (second)
- Szekeres snark
- Tietze graph
- Watkins snark
星
星 Skは任意のkについて完全2部グラフ K1,kの総称である。S3は爪とも呼ばれる。

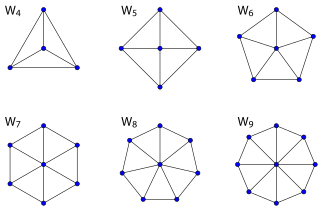
車輪グラフ
車輪グラフ Wnはn個の頂点を持ち、一つの頂点が(n − 1)-閉路グラフのすべての頂点と結ばれたものを言う。
Remove ads
脚注
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads