볼록 해석학

볼록 해석학(convex analysis)은 수학의 한 분야로, 볼록 함수와 볼록 집합의 속성을 연구하는 학문이며, 종종 최적화 이론의 하위 영역인 볼록 최소화에 응용된다.

3차원 볼록 다면체. 볼록 해석학은 유클리드 공간의 볼록 부분집합 연구뿐만 아니라 추상 공간의 볼록 함수 연구도 포함한다.

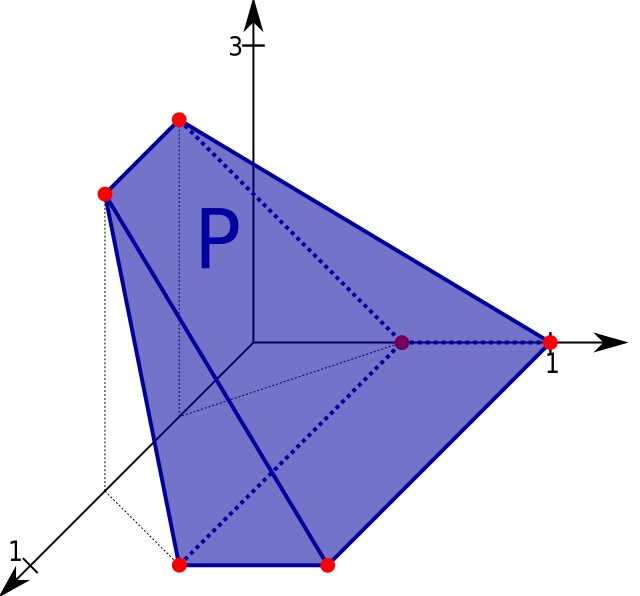
볼록 집합

 이 부분의 본문은 볼록 집합입니다.

일부 벡터 공간 ${\displaystyle X}$의 부분집합 ${\displaystyle C\subseteq X}$는 다음 동등한 조건 중 하나를 만족하면 볼록이다.

1. 만약 ${\displaystyle 0\leq r\leq 1}$이 실수이고 ${\displaystyle x,y\in C}$이면 ${\displaystyle rx+(1-r)y\in C.}$^[1]
2. 만약 ${\displaystyle 0<r<1}$이 실수이고 ${\displaystyle x\neq y}$인 ${\displaystyle x,y\in C}$이면 ${\displaystyle rx+(1-r)y\in C.}$

구간 위에서의 볼록 함수.

 이 부분의 본문은 볼록 함수입니다.

전체적으로, ${\displaystyle f:X\to [-\infty ,\infty ]}$는 벡터 공간의 볼록 부분집합인 정의역 ${\displaystyle \operatorname {domain} f=X}$를 가지는 확장된 실수 ${\displaystyle [-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}}$의 값을 가지는 사상이다. 사상 ${\displaystyle f:X\to [-\infty ,\infty ]}$는 다음이 성립하면 볼록 함수이다.

${\displaystyle f(rx+(1-r)y)\leq rf(x)+(1-r)f(y)}$

(Convexity ≤)

이는 ${\displaystyle 0<r<1}$인 임의의 실수와 ${\displaystyle x\neq y}$인 임의의 ${\displaystyle x,y\in X}$에 대해 성립한다. 만약 정의 부등식 (Convexity ≤)이 엄격한 부등식으로 대체되어도 ${\displaystyle f}$에 대해 이가 여전히 참이면

${\displaystyle f(rx+(1-r)y)<rf(x)+(1-r)f(y)}$

(Convexity <)

${\displaystyle f}$는 엄격하게 볼록하다고 한다.^[1]

볼록 함수는 볼록 집합과 관련이 있다. 특히, 함수 ${\displaystyle f}$는 그 후그래프가

함수 (검은색)는 그 그래프 위의 영역 (초록색)인 후그래프가 볼록 집합인 경우에만 볼록이다.

이변수 볼록 함수 ${\displaystyle x^{2}+xy+y^{2}}$의 그래프.

${\displaystyle \operatorname {epi} f:=\left\{(x,r)\in X\times \mathbb {R} ~:~f(x)\leq r\right\}}$

(Epigraph def.)

볼록 집합인 경우에만 볼록이다.^[2] 확장된 실수값 함수의 후그래프는 실해석학에서 실수값 함수의 그래프가 하는 역할과 유사한 역할을 볼록 해석학에서 한다. 특히, 확장된 실수값 함수의 후그래프는 추측을 공식화하거나 증명하는 데 도움이 될 수 있는 기하학적 직관을 제공한다.

함수 ${\displaystyle f:X\to [-\infty ,\infty ]}$의 정의역은 ${\displaystyle \operatorname {domain} f}$로 표시되는 반면, 그 유효 정의역은 집합이다.^[2]

${\displaystyle \operatorname {dom} f:=\{x\in X~:~f(x)<\infty \}.}$

(dom f def.)

함수 ${\displaystyle f:X\to [-\infty ,\infty ]}$는 ${\displaystyle \operatorname {dom} f\neq \varnothing }$이고 모든 ${\displaystyle x\in \operatorname {domain} f}$에 대해 ${\displaystyle f(x)>-\infty }$인 경우 유효하다고 한다.^[2] 다르게 말하면, 이는 ${\displaystyle f}$의 정의역에 ${\displaystyle f(x)\in \mathbb {R} }$인 ${\displaystyle x}$가 존재하고, ${\displaystyle f}$가 결코 ${\displaystyle -\infty }$와 같지 않음을 의미한다. 즉, 함수가 유효하다는 것은 정의역이 비어 있지 않고, ${\displaystyle -\infty }$ 값을 취하지 않으며, ${\displaystyle +\infty }$와 항등적으로 같지 않다는 것이다. 만약 ${\displaystyle f:\mathbb {R} ^{n}\to [-\infty ,\infty ]}$가 유효 볼록 함수라면, ${\displaystyle b\in \mathbb {R} ^{n}}$인 어떤 벡터와 ${\displaystyle r\in \mathbb {R} }$인 어떤 실수가 존재하여

${\displaystyle f(x)\geq x\cdot b-r}$     모든 ${\displaystyle x}$에 대해

여기서 ${\displaystyle x\cdot b}$는 이들 벡터의 스칼라곱을 나타낸다.

볼록 켤레

 이 부분의 본문은 볼록 켤레 함수입니다.

확장된 실수값을 가지는 함수 ${\displaystyle f:X\to [-\infty ,\infty ]}$(반드시 볼록일 필요는 없음)의 볼록 켤레는 ${\displaystyle X}$의 (연속) 쌍대 공간 ${\displaystyle X^{*}}$에서 ${\displaystyle [-\infty ,\infty ]}$로 가는 함수 ${\displaystyle f^{*}:X^{*}\to [-\infty ,\infty ]}$이며,^[3]

${\displaystyle f^{*}\left(x^{*}\right)=\sup _{z\in X}\left\{\left\langle x^{*},z\right\rangle -f(z)\right\}}$

여기서 괄호 ${\displaystyle \left\langle \cdot ,\cdot \right\rangle }$는 정준 쌍대성 ${\displaystyle \left\langle x^{*},z\right\rangle$ :=x^{*}(z)} 를 나타낸다. 만약 ${\displaystyle \operatorname {Func} (X;Y)}$가 ${\displaystyle X}$ 위의 ${\displaystyle Y}$-값 함수의 집합을 나타낸다면, ${\displaystyle f\mapsto f^{*}}$로 정의되는 사상 ${\displaystyle \operatorname {Func} (X;[-\infty ,\infty ])\to \operatorname {Func} \left(X^{*};[-\infty ,\infty ]\right)}$는 르장드르-펜첼 변환이라고 불린다.

준미분 집합과 펜첼-영 부등식

만약 ${\displaystyle f:X\to [-\infty ,\infty ]}$이고 ${\displaystyle x\in X}$이면 준미분 집합은

${\displaystyle {\begin{alignedat}{4}\partial f(x):&=\left\{x^{*}\in X^{*}~:~f(z)\geq f(x)+\left\langle x^{*},z-x\right\rangle {\text{ for all }}z\in X\right\}&&({\text{“}}z\in X{\text{''}}{\text{ can be replaced with: }}{\text{“}}z\in X{\text{ such that }}z\neq x{\text{''}})\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)\geq \left\langle x^{*},z\right\rangle -f(z){\text{ for all }}z\in X\right\}&&\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)\geq \sup _{z\in X}\left\langle x^{*},z\right\rangle -f(z)\right\}&&{\text{ The right hand side is }}f^{*}\left(x^{*}\right)\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)=f^{*}\left(x^{*}\right)\right\}&&{\text{ Taking }}z:=x{\text{ in the }}\sup {}{\text{ gives the inequality }}\leq .\\\end{alignedat}}}$

예를 들어, ${\displaystyle f=\|\cdot \|}$가 ${\displaystyle X}$의 노름인 중요한 특수 경우에,^{[proof 1]} ${\displaystyle 0\neq x\in X}$이면 이 정의는 다음으로 축소된다는 것을 보일 수 있다.

${\displaystyle \partial f(x)=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle =\|x\|{\text{ and }}\left\|x^{*}\right\|=1\right\}}$     그리고     ${\displaystyle \partial f(0)=\left\{x^{*}\in X^{*}~:~\left\|x^{*}\right\|\leq 1\right\}.}$

모든 ${\displaystyle x\in X}$와 ${\displaystyle x^{*}\in X^{*}}$에 대해, ${\displaystyle f(x)+f^{*}\left(x^{*}\right)\geq \left\langle x^{*},x\right\rangle ,}$ 이는 펜첼-영 부등식이라고 불린다. 이 부등식은 ${\displaystyle x^{*}\in \partial f(x)}$인 경우에만 등식 (즉, ${\displaystyle f(x)+f^{*}\left(x^{*}\right)=\left\langle x^{*},x\right\rangle }$)이 된다. 이런 방식으로 준미분 집합 ${\displaystyle \partial f(x)}$는 볼록 켤레 ${\displaystyle f^{*}\left(x^{*}\right)}$와 직접적으로 관련되어 있다.

이중 켤레

함수 ${\displaystyle f:X\to [-\infty ,\infty ]}$의 이중 켤레는 일반적으로 ${\displaystyle f^{**}:X\to [-\infty ,\infty ]}$로 표기되며, 켤레 함수의 켤레이다. 즉, 모든 ${\displaystyle x\in X}$에 대해 ${\displaystyle f^{**}(x):=\sup _{z^{*}\in X^{*}}\left\{\left\langle x,z^{*}\right\rangle -f^{*}\left(z^{*}\right)\right\}}$이다. 이중 켤레는 강한 또는 약한 쌍대성이 언제 성립하는지 (섭동 함수를 통해) 보여주는 데 유용하다.

모든 ${\displaystyle x\in X}$에 대해 부등식 ${\displaystyle f^{**}(x)\leq f(x)}$는 펜첼-영 부등식에서 비롯된다. 유효 함수의 경우, 펜첼-모로 정리에 따라 ${\displaystyle f}$가 볼록이고 하반연속일 필요충분조건으로 ${\displaystyle f=f^{**}}$가 성립한다.^[3][4]

볼록 최소화

 이 부분의 본문은 볼록 최적화입니다.

볼록 최소화 (원시) 문제는 볼록 함수 ${\displaystyle f:X\to [-\infty ,\infty ]}$와 볼록 부분집합 ${\displaystyle M\subseteq X}$가 주어졌을 때 다음 형태의 문제를 찾는 것이다.

${\displaystyle \inf _{x\in M}f(x)}$를 찾아라.

쌍대 문제

 이 부분의 본문은 쌍대성 (최적화)입니다.

최적화 이론에서 쌍대성 원리는 최적화 문제를 원시 문제 또는 쌍대 문제라는 두 가지 관점에서 볼 수 있다고 말한다.

일반적으로 두 쌍대 짝 분리된 국소 볼록 공간 ${\displaystyle \left(X,X^{*}\right)}$와 ${\displaystyle \left(Y,Y^{*}\right)}$가 주어졌다고 하자. 그러면 함수 ${\displaystyle f:X\to [-\infty ,\infty ]}$가 주어졌을 때, 원시 문제를 ${\displaystyle x}$를 찾아 다음을 만족하는 문제로 정의할 수 있다.

${\displaystyle \inf _{x\in X}f(x).}$

제약 조건이 있다면, 이는 ${\displaystyle f=f+I_{\mathrm {constraints} }}$로 설정하여 함수 ${\displaystyle f}$에 포함시킬 수 있으며, 여기서 ${\displaystyle I}$는 지시 함수이다. 그리고 ${\displaystyle F(x,0)=f(x)}$가 되는 섭동 함수 ${\displaystyle F:X\times Y\to [-\infty ,\infty ]}$를 정의한다.^[5]

선택된 섭동 함수에 대한 쌍대 문제는 다음으로 주어진다.

${\displaystyle \sup _{y^{*}\in Y^{*}}-F^{*}\left(0,y^{*}\right)}$

여기서 ${\displaystyle F^{*}}$는 ${\displaystyle F}$의 두 변수에 대한 볼록 켤레이다.

쌍대성 간격은 다음 부등식의 우변과 좌변의 차이이다.^[6][5][7]

${\displaystyle \sup _{y^{*}\in Y^{*}}-F^{*}\left(0,y^{*}\right)\leq \inf _{x\in X}F(x,0).}$

이 원리는 약한 쌍대성과 동일하다. 만약 두 변이 서로 같다면, 이 문제는 강한 쌍대성을 만족한다고 한다.

강한 쌍대성이 성립하기 위한 많은 조건들이 있다. 예를 들면:

• ${\displaystyle F=F^{**}}$ 여기서 ${\displaystyle F}$는 원시 문제와 쌍대 문제를 연결하는 섭동 함수이고 ${\displaystyle F^{**}}$는 ${\displaystyle F}$의 이중 켤레이다.
• 원시 문제가 선형 최적화 문제이다.
• 볼록 최적화 문제에 대한 슬레이터 조건.^[8][9]

라그랑주 쌍대성

부등식 제약 조건이 있는 볼록 최소화 문제의 경우,

${\displaystyle \min {}_{x}f(x)}$ 제약 조건 ${\displaystyle g_{i}(x)\leq 0}$ (${\displaystyle i=1,\ldots ,m}$).

라그랑주 쌍대 문제는 다음과 같다.

${\displaystyle \sup {}_{u}\inf {}_{x}L(x,u)}$ 제약 조건 ${\displaystyle u_{i}(x)\geq 0}$ (${\displaystyle i=1,\ldots ,m}$).

여기서 목적 함수 ${\displaystyle L(x,u)}$는 다음과 같이 정의되는 라그랑주 쌍대 함수이다.

${\displaystyle L(x,u)=f(x)+\sum _{j=1}^{m}u_{j}g_{j}(x)}$

같이 보기

• 경제학에서의 볼록성
  • 비볼록성 (경제학)
• 볼록성 주제 목록
• 베르너 펜첼