상위 질문
타임라인
채팅
관점

체크메이트

위키백과, 무료 백과사전

체크메이트
Remove ads
다른 뜻에 대해서는 체크메이트 (동음이의) 문서를 참고하십시오.

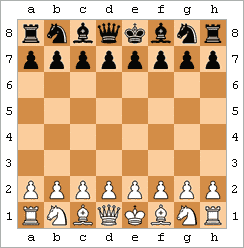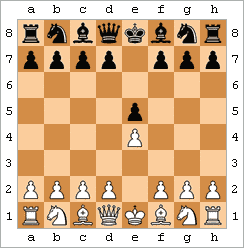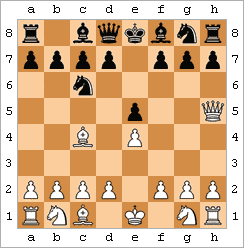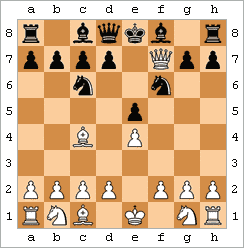
체크메이트 또는 줄여서 메이트는 체스 및 기타 체스 유사 게임에서 플레이어의 킹이 체크 상태에 있고(포획 위협을 받으며) 탈출할 수 있는 방법이 없는 모든 게임 포지션을 의미한다. 상대를 체크메이트하면 게임에서 승리한다.

Thumb
흑이 체크메이트되어 게임에서 패배한다.

체스에서 킹은 실제로 포획되지 않는다. 플레이어는 킹이 체크메이트되는 즉시 패배한다. 공식 경기에서는 필연적으로 패배한 게임은 체크메이트되기 전에 기권하는 것이 일반적으로 좋은 에티켓으로 간주된다.[1][2]

만약 플레이어가 체크 상태가 아니지만 합법적인 수가 없다면, 이는 스테일메이트이며 게임은 즉시 화국으로 끝난다. 체크메이트 수는 대수기보법에서 해시 기호 "#"를 사용하여 기록된다. 예를 들어: 34.Qg3#.

이 문서는 체스 기보에 대수기보법을 사용합니다.
Remove ads

예시

체크메이트는 모든 기물이 아직 보드 위에 있는 상태에서 한 쪽이 단 두 수 만에 발생할 수도 있고(바보 메이트와 같이 게임의 오프닝 단계에서), 미들게임 포지션에서 발생할 수도 있으며(도널드 번과 보비 피셔 간의 1956년 경기인 세기의 게임과 같이),[3] 또는 엔드게임 포지션에서 단 세 개의 기물만으로 여러 수 후에 발생할 수도 있다.

어원

체크메이트(checkmate)라는 용어는 반하트 어원 사전에 따르면 "샤 마트"(페르시아어: شاه مات)라는 페르시아어 문구가 변형된 것으로, "왕은 무력하다"라는 뜻이다.[4] 페르시아어 "마트(māt)"는 왕에게 적용되지만, 산스크리트어 "마타(māta)"(역시 "마트"로 발음)는 왕국이 적에게 "철저히 횡단, 측정, 분배"되었다는 의미로 적용되었다. "마타"는 동사 "마(mā)"의 과거 분사이다.[5] 다른 사람들은 아랍 세계를 통해 체스가 유럽에 전해졌고, 아랍어 마타(아랍어: مَاتَ)가 "죽었다" 또는 "죽었다"는 뜻이므로 "왕은 죽었다"는 의미라고 주장한다.[6][7] 모가담은 '메이트(mate)'라는 단어의 어원을 추적했다. 이 단어는 "남아있다"를 의미하는 페르시아어 동사 만단(페르시아어: ماندن)에서 유래했으며, 이는 라틴어 maneō와 그리스어 메노(고대 그리스어: μένω, "나는 남아있다"를 의미)와 동족이다. 이는 "버려진"이라는 의미로 "남아있다"는 뜻이며, 공식적인 번역은 "놀란"으로, 군사적인 의미에서는 "기습당한"이다.[8] "샤"(페르시아어: شاه)는 군주를 의미하는 페르시아어 단어이다. 플레이어들은 왕이 체크 상태에 있을 때 "샤"라고 외치곤 했다. "마트"(페르시아어: مات)는 "곤경에 처한", "무력한", 또는 "패배한"을 의미하는 페르시아어 형용사이다. 따라서 왕이 기습당하고, 곤경에 처하고, 무력하고, 패배하거나, 자신의 운명에 버려지면 메이트 상태가 된다.[9]

현대 페르시아어에서 '메이트'라는 단어는 얼어붙어 입을 벌린 채 멍하니 쳐다보고 혼란스러워 반응하지 못하는 사람을 묘사한다. '멍해진(stupefied)' 또는 '기절한(stunned)'이라는 단어와 밀접한 상관관계를 가진다. 따라서 '메이트'를 "응답할 수 없는"으로 해석하는 것도 가능하다. 왕이 메이트(샤-마트) 상태에 있다는 것은 왕이 응답할 수 없음을 의미하며, 이는 상대방의 마지막 수에 대해 플레이어의 킹이 할 수 있는 응답이 없다는 것과 일치한다. 이 해석은 킹을 죽이는 것이 아니라 항복 외에는 실행 가능한 응답을 남겨두지 않는다는 게임의 원래 의도에 훨씬 더 가깝고, 이는 샤나메에 자세히 설명된 기원 이야기와 더 잘 일치한다.

현대 용법에서 체크메이트라는 용어는 반박할 수 없는 전략적 승리를 의미하는 은유이다.[10]

Remove ads

역사

초기 산스크리트 체스(약 500~700년)에서는 킹이 포획될 수 있었고, 이것으로 게임이 종료되었다. 페르시아인들(약 700~800년)은 킹이 공격받고 있다는 경고(현대 용어로 체크를 선언하는 것)의 개념을 도입했다. 이는 게임의 조기 및 우발적인 종료를 피하기 위한 것이었다. 나중에 페르시아인들은 킹이 체크 상태로 이동되거나 체크 상태에 남겨질 수 없다는 추가 규칙을 도입했다. 결과적으로 킹은 포획될 수 없었으며,[11] 체크메이트는 게임을 끝내는 유일한 결정적인 방법이 되었다.[12]

약 1600년 이전에는 상대방의 모든 기물을 포획하여 킹 하나만 남기는 것으로도 게임에서 이길 수 있었다. 이 플레이 방식은 현재 전멸(annihilation) 또는 로바도(robado)라고 불린다.[13] 중세 시대에 플레이어들은 체크메이트로 이기는 것을 더 고귀하다고 여기기 시작했고, 그래서 전멸은 잠시 동안 준승(half-win)이 되었다가 결국 폐지되었다.[12]

두 개의 주요 기물

두 개의 주요 기물(퀸 또는 룩)은 래더 체크메이트라고 알려진 기술을 사용하여 보드 가장자리에서 쉽게 메이트를 강요할 수 있다.[14] 이 과정은 두 기물을 인접한 행 또는 열에 배치하고, 한 기물로 킹을 체크하고 다른 기물로 킹이 보드 위로 올라가는 것을 차단하여 킹을 보드 가장자리로 강제하는 것이다.[15] 그림에서 백은 흑 킹을 한 줄씩 가장자리로 몰아넣어 체크메이트한다. 래더 체크메이트는 두 개의 룩, 두 개의 퀸, 또는 룩과 퀸으로 체크메이트하는 데 사용될 수 있다.[15]

Thumb
퀸과 룩을 이용한 체크메이트. 1.Qg5+ Ke4 2.Rf4+ Ke3 3.Qg3+ Ke2 4.Rf2+ Ke1 5.Qg1#[16]

기본 체크메이트

요약
관점

한쪽이 킹만 가지고 있고 다른 쪽이 체크메이트를 강제하는 데 필요한 최소한의 기물만 가지고 있을 때 네 가지 기본적인 체크메이트가 있다. 즉, (1) 한 퀸, (2) 한 룩, (3) 서로 다른 색깔의 칸에 있는 두 비숍, 또는 (4) 비숍과 나이트이다. 킹은 이 모든 체크메이트를 달성하는 데 도움을 주어야 한다.[17] 이기는 쪽이 더 많은 기물을 가지고 있다면 체크메이트는 더 쉽다.

퀸을 이용한 체크메이트가 가장 흔하고 달성하기 쉽다. 이는 종종 폰이 퀸으로 승진한 후에 발생한다. 룩을 이용한 체크메이트도 흔하지만, 두 비숍을 이용하거나 비숍과 나이트를 이용한 체크메이트는 드물게 발생한다. 두 비숍 체크메이트는 비교적 달성하기 쉽지만, 비숍과 나이트 체크메이트는 어렵고 정밀함을 요구한다.

킹과 퀸

처음 두 다이어그램은 퀸을 사용한 기본적인 체크메이트 포지션을 보여준다. 이 포지션은 보드의 어느 가장자리에서든 발생할 수 있다. 당연히 정확한 위치는 다이어그램과 다를 수 있다. 첫 번째 체크메이트 포지션에서는 퀸이 상대 킹 바로 앞에 있고 백 킹이 퀸을 보호하고 있다. 두 번째 체크메이트 포지션에서는 킹들이 오포지션 상태이고 퀸이 킹의 행(또는 열)에서 메이트한다.

abcdefgh
8
Thumb
e4 black king
a1 white queen
b1 white king
8
77
66
55
44
33
22
11
abcdefgh
백은 이 위치에서 쉽게 체크메이트한다.

퀸을 가진 쪽이 움직일 때, 최적의 플레이가 이루어진다면 어떤 시작 위치에서든 최대 열 수 안에 체크메이트를 강제할 수 있지만, 보통은 더 적은 수가 필요하다.[20][21] 폰이 방금 퀸으로 승진한 위치에서는 최대 아홉 수가 필요하다.[22]

다이어그램에 있는 위치에서 백은 흑 킹을 사각형 안에 가두고 그 사각형을 줄여 킹을 보드 가장자리로 이동시켜 쉽게 체크메이트한다:

 1. Qf6 Kd5 2. Qe7 Kd4 3. Kc2 Kd5 4. Kc3 Kc6 5. Kc4 Kb6 6. Qd7 Ka6 7. Qb5+[a] Ka7 8. Kc5 Ka8 9. Kc6 Ka7 10. Qb7#[23]

스테일메이트 방지

이기는 쪽은 상대 킹을 스테일메이트 시키지 않도록 조심해야 하며, 수비하는 쪽은 그러한 위치에 들어가고 싶어 한다. 발생할 수 있는 다섯 가지 일반적인 스테일메이트 유형이 있으며, 더 강한 쪽은 이를 피해야 한다. 처음 두 가지는 더 흔하다.[24]

킹과 룩

첫 번째 다이어그램은 룩을 이용한 기본적인 체크메이트 포지션을 보여주는데, 이는 보드의 어느 가장자리에서든 발생할 수 있다. 흑 킹은 보드 가장자리의 어느 칸에든 있을 수 있고, 백 킹은 그와 오포지션에 있으며, 룩은 해당 행이나 열의 어느 칸에서든 체크할 수 있다 (룩이 포획되지 않는다고 가정할 때). 두 번째 다이어그램은 킹들이 오포지션 상태가 아니지만 수비하는 킹이 코너에 있어야 하는 약간 다른 위치를 보여준다.

룩을 가진 쪽이 움직일 때, 어떤 시작 위치에서든 최대 16수 안에 체크메이트를 강제할 수 있다.[24] 다시, 킹과 룩 대 킹 메이트가 어떻게 달성되는지 시연을 보려면 위키북스 – Chess/The Endgame을 참조하라.

세 번째 다이어그램 위치에서 백은 흑 킹을 사각형 안에 가두고 그 사각형을 줄여 킹을 보드 가장자리로 몰아넣어 체크메이트한다:

1. Kd3+ Kd5 2. Re4 Kd6 3. Kc4! Kc6 4. Re6+ Kc7 5. Kc5 Kd7 6. Kd5 Kc7 7. Rd6 Kb7 8. Rc6 Ka7 9. Kc5 Kb7 10. Kb5 Ka7 11. Rb6 Ka8 12. Kc6 Ka7 13. Kc7 Ka8 14. Ra6# (두 번째 체크메이트 위치, 회전됨).[26]

스테일메이트 방지

스테일메이트 패턴은 두 가지이다.[27]

킹과 두 비숍

두 비숍 체크메이트는 상대방의 두 비숍과 킹에 의해 외로운 킹이 체크메이트되는 것이다.[b] 우세한 쪽은 외로운 킹을 코너로 몰아넣고 두 비숍과 킹이 협력하여 메이트를 강요할 수 있다. 유일한 조건은 두 비숍이 서로 다른 색깔의 칸을 이동해야 한다는 것이다.[c][29] 메이트를 달성하는 데 최대 19수가 필요하다.

두 비숍을 이용한 체크메이트

킹과 비숍들은 협력하여 적 킹을 보드 가장자리로 몰아넣은 다음 코너로 몰아넣어 메이트를 전달한다.[28] "그 과정은 다소 길지만, 열린 보드에서 두 비숍의 힘을 엿볼 수 있게 해주기 때문에 매력적이다."[30]

두 비숍 체크메이트를 통해 세 가지 기본적인 체크메이트 위치가 가능하다.[31] 첫 번째는 코너에서의 체크메이트이다. 두 번째 위치는 코너 칸 옆의 옆 칸에서의 체크메이트이다(이 위치는 이론적으로 가장자리의 어디에서든 발생할 수 있지만, 코너에 인접한 곳에서만 강제될 수 있다). 비숍을 가진 쪽이 움직일 때, 매우 드문 위치(가능한 위치의 0.03%)를 제외하고는 최대 19수 안에 체크메이트를 강제할 수 있다.[32][33] 세 번째 체크메이트 위치는 가능하지만 강제할 수는 없다.[31]

킹의 도움을 받아 두 비숍이 체크메이트를 강요하는 것은 그리 어렵지 않다. 다음 두 가지 원칙이 적용된다.

  • 비숍들은 보드의 중앙 근처, 그리고 인접한 대각선에 있을 때 가장 좋다. 이것은 상대 킹을 차단한다.
  • 킹은 비숍과 함께 공격적으로 사용되어야 한다.
세이라완에서 인용
abcdefgh
8
Thumb
d4 black king
c1 white bishop
d1 white king
f1 white bishop
8
77
66
55
44
33
22
11
abcdefgh
두 비숍과 킹은 메이트를 강요할 수 있다.

세이라완의 포지션에서 백은 흑 킹을 보드의 한쪽으로 몰아넣고, 다시 코너로 몰아넣어 체크메이트로 승리한다. 이는 보드의 어느 쪽이든, 어느 코너든 가능하다. 그 과정은 다음과 같다.

1. Ke2 Ke4 (흑은 킹을 중앙 근처에 두려고 한다) 2. Be3 Ke5 (킹을 뒤로 강제하는데, 이는 자주 발생한다) 3. Kd3 Kd5 4. Bd4 Ke6 5. Ke4 Kd6 (흑은 중앙 근처에 머무르기 위해 다른 접근 방식을 시도한다) 6. Bc4 (백은 좋은 위치에 있다; 비숍들은 중앙에 있고 킹은 활동적이다) 6... Kc6 (흑은 옆으로 가는 것을 피한다) 7. Ke5 Kd7 (흑은 a8-코너를 피하려고 한다) 8. Bd5 (흑 킹을 c6에 못 가게 한다) 8... Kc7 9. Bc5 Kd7 10. Bd6! (킹을 보드 가장자리로 몰아넣는 중요한 수) 10... Ke8 (흑은 여전히 코너를 피한다) 11. Ke6 (이제 흑 킹은 보드 가장자리를 벗어날 수 없다) 11... Kd8 12. Bc6 (킹을 코너 쪽으로 강제한다) 12... Kc8 (흑 킹은 c8과 d8에 갇힌다; 백 킹은 a7과 b7을 커버해야 한다) 13. Kd5 (13. Ke7?는 스테일메이트이다) 13... Kd8 14. Kc5 Kc8 15. Kb6 Kd8 (이제 백은 킹이 코너로 이동하는 것을 허용해야 한다) 16. Bc5 Kc8 17. Be7! (킹을 코너 쪽으로 강제하는 중요한 수) 17... Kb8 18. Bd7! (이전 수와 같은 원리) 18... Ka8 19. Bd8 (백은 템포를 포기하는 수를 두어야 한다; 이 수는 Bc5, Bf8, Be6 또는 Ka6과 함께 그러한 수이다) 19... Kb8 20. Bc7+ Ka8 21. Bc6# (이 섹션의 첫 번째 다이어그램과 같이).[34]

이것은 이 위치에서 강제 체크메이트 중 가장 짧은 것은 아니다. 뮐러와 람프레히트는 15수 솔루션을 제시하지만, 흑의 부정확한 수(엔드게임 테이블베이스에 따르면)가 포함되어 있다.[32]

스테일메이트 방지

실만에서 인용
abcdefgh
8
Thumb
a8 black king
c7 white bishop
b6 black cross
c6 white king
c4 white bishop
8
77
66
55
44
33
22
11
abcdefgh
1.Kb6는 스테일메이트가 된다.


스테일메이트의 한 가지 예시는 이 위치이며, 여기서 1.Kb6 (x로 표시됨)는 스테일메이트가 될 것이다.[35]

킹, 비숍, 나이트

 이 부분의 본문은 비숍과 나이트 체크메이트입니다.

기본 체크메이트 중 이것이 가장 강제하기 어려운 이유는 이 두 기물이 멀리서 적 킹에 대한 선형 방어막을 형성할 수 없기 때문이다. 또한, 체크메이트는 비숍이 제어하는 코너에서만 강제될 수 있다.[33][36]

비숍과 나이트를 이용한 체크메이트

비숍과 나이트, 또는 비숍과 나이트 체크메이트를 사용한 두 가지 기본적인 체크메이트 위치가 표시되어 있다.[37] 첫 번째 위치는 비숍에 의한 체크메이트로, 흑 킹은 코너에 있다. 비숍은 대각선을 따라 다른 칸에도 있을 수 있고, 백 킹과 나이트는 g8과 h7을 공격하는 칸에 있어야 한다. 두 번째 위치는 나이트에 의한 체크메이트로, 흑 킹은 코너 옆의 옆 칸에 있다. 나이트는 흑 킹을 체크하는 다른 칸에 있을 수 있다. 백 킹은 비숍을 보호하고 나이트가 커버하지 않는 칸을 커버하는 칸에 있어야 한다.

비숍과 나이트를 가진 쪽이 움직일 때, 포크로 비숍과 나이트를 동시에 공격하여 둘 다 방어할 수 없는 경우를 제외하고는 어떤 시작 위치에서든 최대 33수 안에 체크메이트를 강제할 수 있다.[38] 그러나 메이팅 과정은 정확한 플레이를 요구하는데, 몇 가지 실수는 화국(50수 규칙 또는 스테일메이트에 의해)으로 이어질 수 있기 때문이다.

이 체크메이트 절차를 배워야 하는지에 대한 의견은 다르다. 제임스 하웰은 그의 책에서 두 비숍을 이용한 체크메이트는 거의 발생하지 않기 때문에 생략하지만, 비숍과 나이트 체크메이트는 포함한다. 하웰은 자신이 세 번 경험했으며(항상 수비하는 쪽에서), 두 비숍을 이용한 체크메이트보다 더 자주 발생한다고 말한다.[39] 반면에 제러미 실먼은 두 비숍을 이용한 체크메이트는 포함하지만 비숍과 나이트 체크메이트는 포함하지 않는데, 그는 단 한 번만 경험했고 그의 친구 존 왓슨은 한 번도 경험하지 못했기 때문이다.[40] 실먼은 다음과 같이 말한다: "...그것을 마스터하는 데는 상당한 시간이 걸릴 것이다. 체스를 희망하는 사람이 평생에 한두 번밖에 달성하지 못할 엔드게임을 배우기 위해 그가 체스 공부를 위해 아껴둔 귀한 시간의 상당 부분을 정말로 소비해야 할까?"

스테일메이트 방지

abcdefgh
8
Thumb
a3 white knight
c3 white king
b1 black king
d1 white bishop
8
77
66
55
44
33
22
11
abcdefgh
1.Na3+? 후, 1...Kc1!은 화국을 만든다.

이 위치는 1966년 A. H. 브랜턴의 엔드게임 연구 끝부분에서 나온 스테일메이트의 한 예시이다. 백은 방금 1.Na3+?를 두었다. 흑이 1...Kc1!을 둔다면, 백은 비숍을 살리기 위해 비숍을 움직여야 하는데, 만약 비숍이 포획되면 기물이 부족하여 무승부가 되기 때문이다. 그러나 어떤 비숍 수를 두더라도 위치는 스테일메이트가 된다.[41]

Remove ads

흔한 체크메이트

요약
관점

백-랭크 메이트

 이 부분의 본문은 백-랭크 체크메이트입니다.
버제스, p. 16
abcdefgh
8
Thumb
d8 black cross
g8 black king
d7 white rook
f7 black pawn
g7 black pawn
h7 black pawn
e1 white king
8
77
66
55
44
33
22
11
abcdefgh
백은 1.Rd8#으로 승리한다.


백-랭크 체크메이트는 룩이나 퀸이 후방 열(즉, 게임 시작 시 기물(폰이 아닌)이 서 있는 줄)을 따라 체크메이트하는 것으로, 체크메이트된 킹이 보드 위로 이동할 수 없는 이유는 킹이 두 번째 열에 있는 아군 기물(보통 폰)에 의해 막혀 있기 때문이다.[42] 백-랭크 체크메이트의 예시가 다이어그램에 나와 있다. 이것은 복도 메이트(corridor mate)로도 알려져 있다.

스콜라 메이트

 이 부분의 본문은 스콜라 메이트입니다.

스콜라 메이트 (또한 4수 체크메이트로도 알려짐)는 다음 수들로 달성되는 체크메이트이다:

1. e4 e5 2. Qh5 Nc6 3. Bc4 Nf6?? 4. Qxf7#

수는 다른 순서로 또는 약간의 변형으로 플레이될 수 있지만, 기본 아이디어는 동일하다: 퀸과 비숍이 f7(또는 흑이 메이트를 수행하는 경우 f2)에 대한 간단한 메이팅 공격에서 결합한다.[43] 네 수만에 체크메이트하는 다른 방법들도 있다.

바보 메이트

 이 부분의 본문은 바보 메이트입니다.

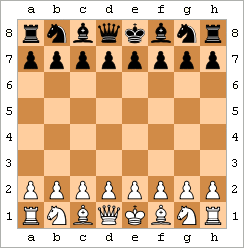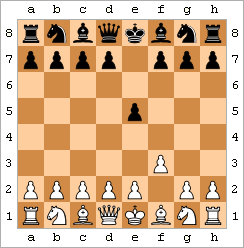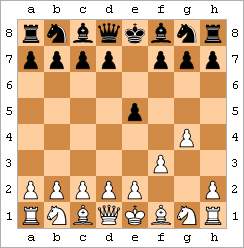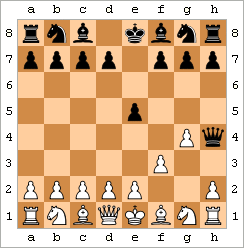
바보 메이트는 2수 체크메이트로도 알려져 있으며, 가장 빠른 체크메이트이다. 대표적인 예시는 다음 수들로 구성된다:

1. f3 e5 2. g4 Qh4#

그 결과 표시된 위치가 된다.[44] (이 패턴은 약간의 변형이 있을 수 있다. 예를 들어 백은 f3 대신 f4를 두거나 g-폰을 먼저 움직일 수 있고, 흑은 ...e5 대신 ...e6을 둘 수 있다.)

스모더드 메이트

 이 부분의 본문은 스모더드 메이트입니다.
팀만 대 쇼트, 1990[45]

스모더드 메이트는 나이트가 킹을 체크메이트하는 것으로, 체크메이트된 킹이 자신의 기물에 둘러싸여(또는 질식되어) 움직일 수 없는 경우이다.[46]

이 메이트는 보통 보드의 코너에서 발생하는데, 킹을 둘러싸는 데 더 적은 기물이 필요하기 때문이다. 가장 흔한 형태의 스모더드 메이트는 인접한 다이어그램에 나와 있다. f7의 나이트가 h8의 킹을 메이트하는데, 킹은 g8의 룩과 g7, h7의 폰 때문에 체크에서 벗어날 수 없다. 마찬가지로 백은 백 킹이 h1에 있고 나이트가 f2에 있을 때 메이트될 수 있다.

Remove ads

드문 체크메이트

요약
관점

일부 드문 포지션에서는 킹과 나이트가 킹과 폰을 상대로 체크메이트를 강제할 수 있다.

스탬마의 메이트

틀:Chess diagram-fen

스탬마의 메이트(필립 스탬마의 이름을 따서 명명됨)를 보여주는 다이어그램에서, 백이 움직일 차례일 때 백이 승리한다.[47]

1. Nb4+ Ka1
2. Kc1 a2
3. Nc2#

흑이 먼저 움직일 차례일 때도 백이 승리한다:

1... Ka1
2. Nc1 a2
3. Nb3#

틀:Chess diagram-fen

이 체크메이트는 2001년 쿠바 체스 챔피언십의 헤수스 노게이라스–마이켈 곤고라 경기에서 발생했다[48] (다이어그램 참조), 경기 진행은 다음과 같다:

81. Kc2 Ka1
82. Nc5 Ka2

만약 82...a2라면 83.Nb3#이다.

83. Nd3

첫 번째 다이어그램의 위치에 도달하며, 흑이 움직일 차례이다.

83... Ka1
84. Nc1 1–0

흑은 여기서 기권했다; 경기는 84...a2 85.Nb3#으로 계속되었을 것이다.[49]

틀:Chess diagram-fen

나이트가 d2에 있는 유사한 포지션은 500년 이상 된 것으로, 루카 파치올리가 1498년 작성한 그의 필사본 'De ludo scachorum'(라틴어로 "체스 게임")에서 "Partito n. 23"으로 확인되었으며, 최근 Aboca Museum Edizioni에서 재출판되었다('Gli scacchi').

1. Nf3 Ka1
2. Nd4 Ka2
3. Ne2 Ka1
4. Nc1 a2
5. Nb3#

특이한 메이트

킹과 나이트가 킹과 비숍, 나이트 또는 룩을 체크메이트할 수 있는 위치가 있거나, 킹과 비숍이 다른 색 칸의 비숍이나 나이트와 함께 킹을 체크메이트할 수 있는 위치가 있지만, 보드에 다른 기물이 없다면 체크메이트를 강제할 수는 없다(예시 다이어그램 참조).[50] 그럼에도 불구하고, 이는 이러한 기물 조합이 FIDE 체스 규칙에 따라 "불충분한 메이팅 기물" 또는 "체크메이트 불가능"으로 인해 화국으로 판정되는 것을 막는다. 미국 체스 연맹 규칙은 다르다. 마이너 기물 대 마이너 기물의 일반적인 위치에서, 플레이어는 남은 시간이 제한적이라면 무승부를 주장할 수 있다.[51]

두 개와 세 개의 나이트

두 나이트
 이 부분의 본문은 투 나이트 엔드게임입니다.

킹과 두 나이트로는 체크메이트를 강제할 수 없지만, 체크메이트 위치는 가능하다(첫 번째 다이어그램 참조). 두 번째 다이어그램에서 흑이 1...Ka8??를 두면 백은 2.Nbc7#으로 체크메이트할 수 있지만, 흑은 1...Kc8을 두어 위협을 피할 수 있다. 수비하는 쪽의 임무는 쉽다. 다음 수에서 체크메이트될 수 있는 위치로 이동하는 것을 피하기만 하면 되고, 그러한 상황에서는 항상 다른 수를 사용할 수 있다.[52]

세 번째 다이어그램에서 한 나이트는 c1을 지키고 있어 다른 나이트가 체크메이트를 시도해야 한다. 1.Ndc3+ Ka1 다음에 백은 e2의 나이트를 c2로 옮겨야 한다. 그러나 백이 2.Nd4를 두면 흑은 스테일메이트가 된다.[53]

어떤 상황에서는 두 나이트와 킹이 킹과 폰(또는 드물게 더 많은 폰)을 상대로 체크메이트를 강제할 수 있다. 실제로 실행하기는 매우 어려운 승리 계획은 나이트 중 하나로 상대 폰을 봉쇄하고, 상대 킹을 스테일메이트 위치로 이동시킨 다음, 다른 나이트를 가져와 체크메이트하는 것이다.[53] (자세한 내용은 투 나이트 엔드게임 참조)

세 나이트

세 나이트와 킹은 외로운 킹을 상대로 20수 이내에 체크메이트를 강제할 수 있다(외로운 킹이 나이트를 빠르게 포획할 수 없다고 가정할 때).[54] 이러한 상황은 일반적으로 체스 문제에서만 볼 수 있는데, 나이트 중 적어도 하나는 승진된 기물이어야 하고, 폰을 퀸 외의 다른 기물로 승진시킬 이유가 거의 없기 때문이다(언더프로모션 참조).

Remove ads

같이 보기

내용주

  1. [a]
    7.Kc5는 두 수 더 빠르게 승리한다.
  2. [b]
    "하나의 나이트나 하나의 비숍을 상대로는 수비자가 원하더라도 패배할 수 없다."[28]
  3. [c]
    언더프로모션만이 같은 색깔의 칸에 비숍이 놓이게 할 수 있다.

각주

Loading related searches...

Wikiwand - on

Seamless Wikipedia browsing. On steroids.

Remove ads
Remove ads