진리 함수

논리학에서 진리 함수(truth function)^[1]는 진릿값을 입력으로 받아 고유한 진릿값을 출력하는 함수이다. 다시 말해, 진리 함수의 입력과 출력은 모두 진릿값이다. 진리 함수는 항상 정확히 하나의 진릿값을 출력하며, 동일한 진릿값(들)을 입력하면 항상 동일한 진릿값이 출력된다. 전형적인 예는 명제 논리에서 복합 명제가 논리 연산으로 연결된 개별 명제들을 사용하여 구성되는 경우이다. 만약 복합 명제의 진릿값이 구성 명제(들)의 진릿값에 의해 전적으로 결정된다면, 복합 명제는 진리 함수라고 불리며, 사용된 모든 논리 연산은 진리 함수적이라고 한다.^[2]

고전 명제 논리는 진리 함수적 논리이다.^[3] 이는 모든 명제가 참 또는 거짓 중 정확히 하나의 진릿값을 가지며, 모든 논리 연산이 진리 함수적(대응하는 진리표를 가짐)이므로 모든 복합 명제가 진리 함수이기 때문이다.^[4] 반면에 양상 논리는 비진리 함수적이다.

개요

복합 문장의 진릿값이 하위 문장의 진릿값의 함수인 경우, 논리 연산은 진리 함수적이다. 논리 연산의 집합은 각 구성원이 진리 함수적일 경우 진리 함수적이다. 예를 들어, "그리고" 연산은 진리 함수적이다. 왜냐하면 "사과는 과일이고 당근은 채소이다"와 같은 문장은 "사과는 과일이다"와 "당근은 채소이다"라는 각 하위 문장이 참일 때만 참이고, 그렇지 않으면 거짓이기 때문이다. 영어와 같은 자연어의 일부 논리 연산은 진리 함수적이 아니다.

"x는 ...라고 믿는다" 형식의 논리 연산은 진리 함수적이 아닌 연산의 전형적인 예이다. 예를 들어 메리가 2000년 4월 20일에 앨 고어가 미국 대통령이었다고 잘못 믿지만, 달이 녹색 치즈로 만들어졌다고는 믿지 않는다고 가정하자. 그렇다면 다음 문장은

"메리는 앨 고어가 2000년 4월 20일에 미국 대통령이었다고 믿는다"

는 참이지만, 다음 문장은

"메리는 달이 녹색 치즈로 만들어졌다고 믿는다"

는 거짓이다. 두 경우 모두, 각 구성 문장(즉, "앨 고어는 2000년 4월 20일에 미국 대통령이었다"와 "달은 녹색 치즈로 만들어졌다")은 거짓이지만, "메리는 ...라고 믿는다"라는 구를 접두사로 붙여 형성된 각 복합 문장은 진릿값이 다르다. 즉, "메리는 ...라고 믿는다" 형식의 문장의 진릿값은 구성 문장의 진릿값만으로는 결정되지 않으므로, (단항) 논리 연산 (또는 단항이므로 단순히 연산자)은 비진리 함수적이다.

공식 구성에 사용되는 고전 논리 연산(예: &, →)은 진리 함수적이다. 인수로 다양한 진릿값을 사용할 때의 값은 일반적으로 진리표로 주어진다. 진리 함수적 명제 논리는 공식이 참 또는 거짓으로 해석될 수 있는 형식 체계이다.

이항 진리 함수 표

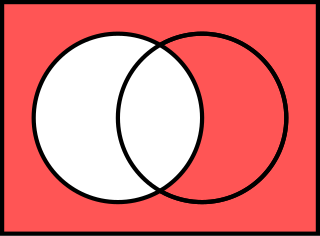
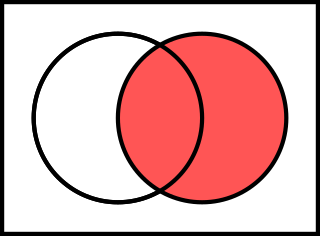
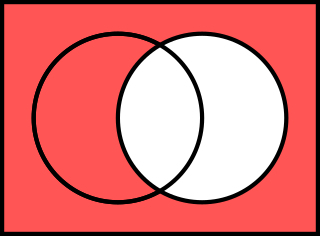
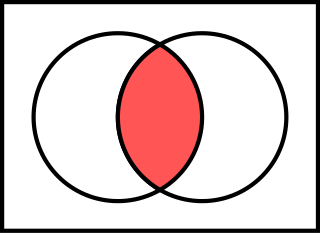
2가 논리에서 두 입력 P와 Q에 대한 16가지 가능한 진리 함수가 있으며, 이를 불 함수라고도 한다. 이 함수들 각각은 고전 논리에서 특정 논리 연산의 진리표에 해당하며, 인수의 하나 또는 둘 모두에 의존하지 않는 함수와 같은 몇 가지 퇴화된 경우도 포함한다. 다음 진리표에서는 간결성을 위해 참은 1, 거짓은 0으로 표시한다.

모순/거짓 Notation Equivalent formulas Truth table Venn diagram ${\displaystyle \bot }$ "bottom" P ∧ ¬P Opq   Q 0 1 P 0    0   0  1    0   0	항진식/참 Notation Equivalent formulas Truth table Venn diagram ${\displaystyle \top }$ "top" P ∨ ¬P Vpq   Q 0 1 P 0    1   1  1    1   1
명제 P Notation Equivalent formulas Truth table Venn diagram P p Ipq   Q 0 1 P 0    0   0  1    1   1	P의 부정 Notation Equivalent formulas Truth table Venn diagram ¬P ~P Np Fpq   Q 0 1 P 0    1   1  1    0   0
명제 Q Notation Equivalent formulas Truth table Venn diagram Q q Hpq   Q 0 1 P 0    0   1  1    0   1	Q의 부정 Notation Equivalent formulas Truth table Venn diagram ¬Q ~Q Nq Gpq   Q 0 1 P 0    1   0  1    1   0
논리곱 Notation Equivalent formulas Truth table Venn diagram P ∧ Q P & Q P · Q P AND Q P ↛¬Q ¬P ↚ Q ¬P ↓ ¬Q Kpq   Q 0 1 P 0    0   0  1    0   1	비논리곱/선택 부정 Notation Equivalent formulas Truth table Venn diagram P ↑ Q P | Q P NAND Q P → ¬Q ¬P ← Q ¬P ∨ ¬Q Dpq   Q 0 1 P 0    1   1  1    1   0
논리합 Notation Equivalent formulas Truth table Venn diagram P ∨ Q P OR Q P ← ¬Q ¬P → Q ¬P ↑ ¬Q ¬(¬P ∧ ¬Q) Apq   Q 0 1 P 0    0   1  1    1   1	비논리합/합동 부정 Notation Equivalent formulas Truth table Venn diagram P ↓ Q P NOR Q P ↚ ¬Q ¬P ↛ Q ¬P ∧ ¬Q Xpq   Q 0 1 P 0    1   0  1    0   0
함축 비포함 Notation Equivalent formulas Truth table Venn diagram P ↛ Q P ${\displaystyle \not \supset }$ Q P ${\displaystyle >}$ Q P NIMPLY Q P ∧ ¬Q ¬P ↓ Q ¬P ↚ ¬Q Lpq   Q 0 1 P 0    0   0  1    1   0	실질 함축 Notation Equivalent formulas Truth table Venn diagram P → Q P ⊃ Q P ${\displaystyle \leq }$ Q P IMPLY Q P ↑ ¬Q ¬P ∨ Q ¬P ← ¬Q Cpq   Q 0 1 P 0    1   1  1    0   1
역 함축 비포함 Notation Equivalent formulas Truth table Venn diagram P ↚ Q P ${\displaystyle \not \subset }$ Q P ${\displaystyle <}$ Q P ↓ ¬Q ¬P ∧ Q ¬P ↛ ¬Q Mpq   Q 0 1 P 0    0   1  1    0   0	역 함축 Notation Equivalent formulas Truth table Venn diagram P ← Q P ⊂ Q P ${\displaystyle \geq }$ Q P ∨ ¬Q ¬P ↑ Q ¬P → ¬Q Bpq   Q 0 1 P 0    1   0  1    1   1
비동치/배타적 논리합 Notation Equivalent formulas Truth table Venn diagram P ↮ Q P ≢ Q P ⨁ Q P XOR Q P 틀:Eqv ¬Q ¬P 틀:Eqv Q ¬P ↮ ¬Q Jpq   Q 0 1 P 0    0   1  1    1   0	동치/쌍조건 Notation Equivalent formulas Truth table Venn diagram P 틀:Eqv Q P ≡ Q P XNOR Q P IFF Q P ↮ ¬Q ¬P ↮ Q ¬P 틀:Eqv ¬Q Epq   Q 0 1 P 0    1   0  1    0   1

함수적 완전성

 이 부분의 본문은 함수적 완전성입니다.

함수는 합성으로 표현될 수 있으므로, 진리 함수적 논리 계산은 함수적으로 완전하기 위해 위에 언급된 모든 함수에 대한 전용 기호를 가질 필요가 없다. 이는 명제 논리에서 특정 복합 명제의 논리적 동치로 표현된다. 예를 들어, 고전 논리에서 ¬P ∨ Q는 P → Q와 동치이다. 따라서 "¬"(부정)와 "∨"(논리합)가 이미 사용 중이라면 조건 연산자 "→"는 고전 기반 논리 체계에 필수적이지 않다.

명제 논리에서 표현 가능한 모든 명제를 표현할 수 있는 최소 연산자 집합을 최소 함수적 완전 집합이라고 한다. 최소 완전 집합의 연산자는 NAND만 {↑} 또는 NOR만 {↓}으로 달성된다.

아리티가 2를 초과하지 않는 최소 함수적 완전 연산자 집합은 다음과 같다.^[5]

하나의 원소

{↑}, {↓}.

두 개의 원소

${\displaystyle \{\vee ,\neg \}}$, ${\displaystyle \{\wedge ,\neg \}}$, ${\displaystyle \{\to ,\neg \}}$, ${\displaystyle \{\gets ,\neg \}}$, ${\displaystyle \{\to ,\bot \}}$, ${\displaystyle \{\gets ,\bot \}}$, ${\displaystyle \{\to ,\nleftrightarrow \}}$, ${\displaystyle \{\gets ,\nleftrightarrow \}}$, ${\displaystyle \{\to ,\nrightarrow \}}$, ${\displaystyle \{\to ,\nleftarrow \}}$, ${\displaystyle \{\gets ,\nrightarrow \}}$, ${\displaystyle \{\gets ,\nleftarrow \}}$, ${\displaystyle \{\nrightarrow ,\neg \}}$, ${\displaystyle \{\nleftarrow ,\neg \}}$, ${\displaystyle \{\nrightarrow ,\top \}}$, ${\displaystyle \{\nleftarrow ,\top \}}$, ${\displaystyle \{\nrightarrow ,\leftrightarrow \}}$, ${\displaystyle \{\nleftarrow ,\leftrightarrow \}}$.

세 개의 원소

${\displaystyle \{\lor ,\leftrightarrow ,\bot \}}$, ${\displaystyle \{\lor ,\leftrightarrow ,\nleftrightarrow \}}$, ${\displaystyle \{\lor ,\nleftrightarrow ,\top \}}$, ${\displaystyle \{\land ,\leftrightarrow ,\bot \}}$, ${\displaystyle \{\land ,\leftrightarrow ,\nleftrightarrow \}}$, ${\displaystyle \{\land ,\nleftrightarrow ,\top \}}$.

대수적 속성

일부 진리 함수는 해당 논리 연산을 포함하는 정리로 표현될 수 있는 속성을 가지고 있다. 이항 진리 함수(또는 해당 논리 연산)가 가질 수 있는 속성 중 일부는 다음과 같다.

• 결합법칙: 같은 결합 연산자가 연속으로 두 개 이상 포함된 식에서, 피연산자의 순서가 바뀌지 않는 한 연산의 순서는 중요하지 않다.
• 교환법칙: 논리 연산의 피연산자는 식의 진릿값에 영향을 주지 않고 서로 바꿀 수 있다.
• 분배법칙: ·로 표시되는 논리 연산이 +로 표시되는 다른 논리 연산에 대해 분배된다는 것은 모든 피연산자 a, b, c에 대해 a · (b + c) = (a · b) + (a · c)가 성립함을 의미한다.
• 멱등법칙: 연산의 피연산자가 동일할 때, 해당 논리 연산은 피연산자를 결과로 반환한다. 다시 말해, 해당 연산은 진리 보존적이면서 거짓 보존적이다(아래 참조).
• 흡수 법칙: 한 쌍의 논리 연산자 ${\displaystyle \land ,\lor }$는 모든 피연산자 a, b에 대해 ${\displaystyle a\land (a\lor b)=a\lor (a\land b)=a}$일 경우 흡수 법칙을 만족한다.

진리 함수 집합은 다음 다섯 가지 속성 각각에 대해 이를 결여하는 구성원을 적어도 하나 포함할 때에만 함수적으로 완전하다.

• 단조: 모든 a₁, ..., a_n, b₁, ..., b_n ∈ {0,1}에 대해 a₁ ≤ b₁, a₂ ≤ b₂, ..., a_n ≤ b_n일 때 f(a₁, ..., a_n) ≤ f(b₁, ..., b_n)이다. 예를 들어, ${\displaystyle \vee ,\wedge ,\top ,\bot }$.
• 아핀: 각 변수에 대해, 다른 모든 변수의 값이 고정되어 있을 때, 해당 변수의 값을 변경하면 연산의 진릿값이 항상 변경되거나 전혀 변경되지 않는다. 예를 들어, ${\displaystyle \neg ,\leftrightarrow }$, ${\displaystyle \not \leftrightarrow ,\top ,\bot }$.
• 자기 쌍대: 연산의 진릿값 할당을 진리표에서 위에서 아래로 읽는 것이 아래에서 위로 읽은 값의 보수를 취하는 것과 같다. 즉, f(¬a₁, ..., ¬a_n) = ¬f(a₁, ..., a_n)이다. 예를 들어, ${\displaystyle \neg }$.
• 진리 보존: 모든 변수가 참의 진릿값으로 할당된 해석이 이러한 연산의 결과로 참의 진릿값을 산출한다. 예를 들어, ${\displaystyle \vee ,\wedge ,\top ,\rightarrow ,\leftrightarrow ,\subset }$. (타당성 참조)
• 거짓 보존: 모든 변수가 거짓의 진릿값으로 할당된 해석이 이러한 연산의 결과로 거짓의 진릿값을 산출한다. 예를 들어, ${\displaystyle \vee ,\wedge ,\nleftrightarrow ,\bot ,\not \subset ,\not \supset }$. (타당성 참조)

항수

 항수 (수학) 문서를 참고하십시오.

구체적인 함수는 연산자로도 지칭될 수 있다. 2가 논리에는 2개의 널항 연산자(상수), 4개의 단항연산, 16개의 이항 연산자, 256개의 삼항 연산자, 그리고 ${\displaystyle 2^{2^{n}}}$개의 n항 연산자가 있다. 3가 논리에는 3개의 널항 연산자(상수), 27개의 단항연산, 19683개의 이항 연산자, 7625597484987개의 삼항 연산자, 그리고 ${\displaystyle 3^{3^{n}}}$개의 n항 연산자가 있다. k가 논리에는 k개의 널항 연산자, ${\displaystyle k^{k}}$개의 단항 연산자, ${\displaystyle k^{k^{2}}}$개의 이항 연산자, ${\displaystyle k^{k^{3}}}$개의 삼항 연산자, 그리고 ${\displaystyle k^{k^{n}}}$개의 n항 연산자가 있다. k가 논리의 n항 연산자는 ${\displaystyle \mathbb {Z} _{k}^{n}\to \mathbb {Z} _{k}}$ 함수이다. 따라서 이러한 연산자의 수는 ${\displaystyle |\mathbb {Z} _{k}|^{|\mathbb {Z} _{k}^{n}|}=k^{k^{n}}}$이며, 위의 숫자들이 여기서 유도되었다.

그러나 특정 항수를 가진 일부 연산자는 실제로 일부 입력에 대해 더 낮은 항수 연산을 수행하고 나머지 입력은 무시하는 퇴화된 형태이다. 위에 언급된 256개의 삼항 불 연산자 중 ${\displaystyle {\binom {3}{2}}\cdot 16-{\binom {3}{1}}\cdot 4+{\binom {3}{0}}\cdot 2}$개는 포함배제의 원리를 사용하여 이항 또는 그 이하 항수 연산자의 퇴화된 형태이다. 삼항 연산자 ${\displaystyle f(x,y,z)=\lnot x}$는 실제로 하나의 입력에 적용되고 다른 두 입력은 무시하는 단항 연산자이다.

"부정"은 단항 연산자이며, 단일 항(¬P)을 취한다. 나머지는 이항 연산자이며, 두 항을 취하여 복합 명제(P ∧ Q, P ∨ Q, P → Q, P ↔ Q)를 만든다.

논리 연산자 집합 Ω는 다음과 같이 서로소 부분 집합으로 분할될 수 있다.

${\displaystyle \Omega =\Omega _{0}\cup \Omega _{1}\cup \ldots \cup \Omega _{j}\cup \ldots \cup \Omega _{m}\,.}$

이 분할에서 ${\displaystyle \Omega _{j}}$는 항수 j의 연산자 기호 집합이다.

더 익숙한 명제 논리에서는 ${\displaystyle \Omega }$가 일반적으로 다음과 같이 분할된다.

널항 연산자: ${\displaystyle \Omega _{0}=\{\bot ,\top \}}$

단항 연산자: ${\displaystyle \Omega _{1}=\{\lnot \}}$

이항 연산자: ${\displaystyle \Omega _{2}\supset \{\land ,\lor ,\rightarrow ,\leftrightarrow \}}$

구성성 원리

진리표를 사용하는 대신, 논리 연산 기호는 의미의 구성성 원리에 의해 상세히 설명된 바와 같이, 해석 함수와 함수적으로 완전한 진리 함수 집합(Gamut 1991)을 통해 해석될 수 있다. I를 해석 함수라 하고, Φ, Ψ를 두 임의의 문장이라 하며, 진리 함수 f_nand를 다음과 같이 정의하자.

• f_nand(T,T) = F; f_nand(T,F) = f_nand(F,T) = f_nand(F,F) = T

그러면 편의를 위해 f_not, f_or, f_and 등은 f_nand를 통해 다음과 같이 정의된다.

• f_not(x) = f_nand(x,x)
• f_or(x,y) = f_nand(f_not(x), f_not(y))
• f_and(x,y) = f_not(f_nand}(x,y))

또는 대안적으로 f_not, f_or, f_and 등은 직접 다음과 같이 정의된다.

• f_not(T) = F; f_not(F) = T;
• f_or(T,T) = f_or(T,F) = f_{or}(F,T) = T; for(F,F) = F}
• f_and(T,T) = T; f_and(T,F) = f_and(F,T) = f_and(F,F) = F

그러면

• I(~) = I(틀:Not) = f_not
• I(&) = I(틀:And) = f_and
• I(v) = I(틀:Or-) = f_or
• I(~Φ) = I(틀:NotΦ) = I(틀:Not)(I(Φ)) = f_not(I(Φ))
• I(Φ틀:AndΨ) = I(틀:And)(I(Φ), I(Ψ)) = f_and(I(Φ), I(Ψ))

등.

따라서 S가 논리 연산자를 나타내는 논리 기호 v₁...v_n과 비논리 기호 c₁...c_n으로 구성된 기호열인 문장이라고 하자. 그러면 I(v₁)...I(v_n)이 f_nand(또는 다른 함수적으로 완전한 진리 함수 집합)를 통해 v₁부터 v_n까지를 해석하도록 제공된 경우에만 ${\displaystyle I(s)}$의 진릿값은 c₁...c_n의 진릿값, 즉 I(c₁)...I(c_n)에 의해 전적으로 결정된다. 다시 말해, 예상대로 S는 모든 비논리 기호의 해석 하에서만 참 또는 거짓이다.

정의

위에 정의된 함수들을 사용하여, 명제의 진리 함수에 대한 형식적인 정의를 내릴 수 있다.^[6]

PROP를 모든 명제 변수의 집합이라고 하자.

${\displaystyle PROP=\{p_{1},p_{2},\dots \}}$

진리 할당은 임의의 함수 ${\displaystyle \phi :PROP\to \{T,F\}}$로 정의한다. 진리 할당은 따라서 각 명제 변수를 특정 진릿값과 연결하는 것이다. 이는 명제의 진리표의 특정 행과 실질적으로 동일하다.

진리 할당 ${\displaystyle \phi }$에 대해, 그 확장된 진리 할당 ${\displaystyle {\overline {\phi }}}$를 다음과 같이 정의한다. 이는 ${\displaystyle \phi }$를 모든 명제 형식의 집합과 동일한 정의역을 갖는 새로운 함수 ${\displaystyle {\overline {\phi }}}$로 확장한다. ${\displaystyle {\overline {\phi }}}$의 치역은 여전히 ${\displaystyle \{T,F\}}$이다.

1. ${\displaystyle A\in PROP}$이면 ${\displaystyle {\overline {\phi }}(A)=\phi (A)}$이다.
2. A와 B가 임의의 명제 형식인 경우,
   1. ${\displaystyle {\overline {\phi }}(\neg A)=f_{\text{not}}({\overline {\phi }}(A))}$이다.
   2. ${\displaystyle {\overline {\phi }}(A\land B)=f_{\text{and}}({\overline {\phi }}(A),{\overline {\phi }}(B))}$이다.
   3. ${\displaystyle {\overline {\phi }}(A\lor B)=f_{\text{or}}({\overline {\phi }}(A),{\overline {\phi }}(B))}$이다.
   4. ${\displaystyle {\overline {\phi }}(A\to B)={\overline {\phi }}(\neg A\lor B)}$이다.
   5. ${\displaystyle {\overline {\phi }}(A\leftrightarrow B)={\overline {\phi }}((A\to B)\land (B\to A))}$이다.

마지막으로, 확장된 진리 할당을 정의했으므로, 이를 사용하여 명제의 진리 함수를 정의할 수 있다. 명제 A에 대한 진리 함수 ${\displaystyle f_{A}}$는 모든 진리 할당의 집합과 동일한 정의역을 가지며, ${\displaystyle \{T,F\}}$를 치역으로 가진다.

이는 각 진리 할당 ${\displaystyle \phi }$에 대해 ${\displaystyle f_{A}(\phi )={\overline {\phi }}(A)}$로 정의된다. ${\displaystyle {\overline {\phi }}(A)}$에 의해 주어진 값은 ${\displaystyle \phi }$로 식별된 행에 있는 A의 진리표의 마지막 열에 표시된 값과 동일하다.

컴퓨터 과학

논리 연산자는 디지털 회로에서 논리 회로로 구현된다. 거의 모든 디지털 회로(주요 예외는 DRAM)는 NAND, NOR, NOT, 그리고 전송 게이트로 구성된다. 일반적으로 2개 입력 대신 3개 이상의 입력을 가진 NAND 및 NOR 게이트는 상당히 일반적이지만, 논리적으로는 2개 입력 게이트의 캐스케이드와 동등하다. 다른 모든 연산자는 위의 2개 이상의 논리 게이트의 논리적으로 동등한 조합으로 분해하여 구현된다.

"NAND만", "NOR만", "NOT과 AND"의 "논리적 동등성"은 튜링 동치와 유사하다.

모든 진리 함수가 NOR만으로 표현될 수 있다는 사실은 아폴로 가이던스 컴퓨터에 의해 입증되었다.

같이 보기

• 버트런드 러셀과 앨프리드 노스 화이트헤드,
  수학 원리, 2판
• 루트비히 비트겐슈타인,
  논리철학 논고, 명제 5.101
• 비트 연산
• 이항 함수
• 불 도메인
• 불 논리
• 불리언 값 함수
• 불 대수학 주제 목록
• 논리 상수
• 양상 연산자
• 명제 논리
• 진리 함수적 명제 논리