모듈러 군

수학에서 모듈러 군(영어: modular group) 또는 보형군(保型群)은 정수 계수의 뫼비우스 변환의 군이다. 무한 이산 군이며, 두 개의 생성원 ${\displaystyle S}$, ${\displaystyle T}$로 주어진다. 기호는 ${\displaystyle \operatorname {PSL} (2,\mathbb {Z} )}$ 또는 ${\displaystyle \Gamma }$.

정의

모듈러 군 ${\displaystyle \Gamma }$는 다음과 같은 표시를 갖는 군이다.

${\displaystyle \Gamma =\langle {\mathsf {S}},{\mathsf {T}}|{\mathsf {S}}^{2}=({\mathsf {S}}{\mathsf {T}})^{3}=1\rangle }$

즉, 이는 2차 순환군과 3차 순환군의 자유곱이다.

${\displaystyle \Gamma =\operatorname {Cyc} (2)\star \operatorname {Cyc} (3)}$

성질

모듈러 군은 가산 무한 개의 원소를 가지는 군이며, 아벨 군이 아니다. 그 중심은 자명군이다.

상반평면 위의 작용

모듈러 군은 상반평면 ${\displaystyle \mathbb {H} =\{\tau \in \mathbb {C} \colon \operatorname {Im} \tau >0\}}$에 유리 함수로 작용한다. 이 경우 생성원 ${\displaystyle {\mathsf {S}}}$, ${\displaystyle {\mathsf {T}}}$의 작용은 다음과 같다.

${\displaystyle {\mathsf {S}}\colon z\mapsto -1/z}$

${\displaystyle {\mathsf {T}}\colon z\mapsto z+1}$

따라서 모듈러 군의 일반적인 원소는 다음과 같이 작용한다.

${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}\colon z\mapsto {\frac {az+b}{cz+d}}}$. (${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2;\mathbb {Z} )}$)

이 경우 행렬 ${\displaystyle +M,-M\in \operatorname {SL} (2;\mathbb {Z} )}$의 작용이 같으므로, 이는 ${\displaystyle \operatorname {SL} (2;\mathbb {Z} )/(-I)=\operatorname {PSL} (2;\mathbb {Z} )=\Gamma }$의 작용임을 알 수 있다.

모듈러 군의 작용의 표준적인 기본 영역(영어: fundamental domain)은 다음과 같다.

${\displaystyle \{z\in \mathbb {H} \colon |\operatorname {Re} (z)|\leq 1/2,\;|z|\geq 1\}}$

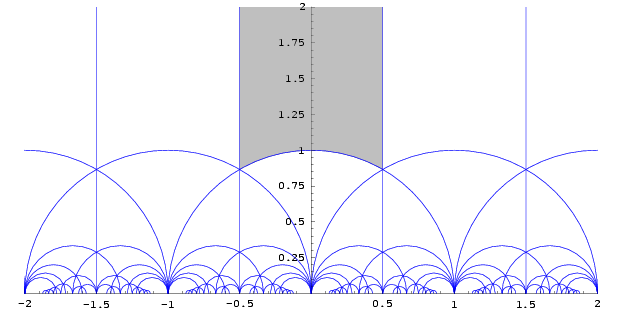
보다 일반적으로, 이 작용은 리만 구의 반구

${\displaystyle \{\tau \in \mathbb {C} \colon \operatorname {Im} \tau \geq 0\}\sqcup \{\infty \}=\mathbb {H} \sqcup \mathbb {P} _{\mathbb {R} }^{1}}$

위로 확장될 수 있다. 이 경우, 이는 실수 사영 직선 ${\displaystyle \mathbb {P} _{\mathbb {R} }^{1}=\mathbb {R} \sqcup \{\infty \}}$ 위에 다음과 같이 따로 작용한다. 사실, 이 작용은 대수적 수의 집합(+∞) 또는 유리수체(+∞)로 제한될 수 있다. 즉, 모듈러 군은 다음과 같은 부분 집합 위에 각각 작용한다.

• ${\displaystyle \mathbb {H} }$ (허수 성분이 양수인 복소수)
• ${\displaystyle \mathbb {R} \setminus {\bar {\mathbb {Q} }}}$ (초월수)
• ${\displaystyle {\bar {\mathbb {Q} }}\cap \mathbb {R} \setminus \mathbb {Q} }$ (대수적 무리수)
• ${\displaystyle \mathbb {Q} \sqcup \{\infty \}}$ (유리수 및 무한대)

유리수체 위의 작용

모듈러 군은 유리수 사영 직선 ${\displaystyle \mathbb {P} _{\mathbb {Q} }^{1}=\mathbb {Q} \sqcup \{\infty \}}$ 위에 작용한다. 구체적으로, 다음과 같은 집합을 생각하자.

${\displaystyle X=\{(p,q)\in \mathbb {Z} ^{2}\colon \gcd\{p,q\}=1,\;pq\neq 0\}}$

그렇다면, 그 위에 ${\displaystyle \operatorname {SL} (2;\mathbb {Z} )}$의 다음과 같은 작용을 정의할 수 있다.

${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}\cdot {\frac {p}{q}}={\frac {ap+bq}{cp+dq}}\qquad \left({\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2;\mathbb {Z} )\right)}$

이 경우, 위 행렬이 특수 선형군에 속하므로 그 행렬식이 1이다. 즉, ${\displaystyle ad-bc=1}$다. 따라서, ${\displaystyle \gcd\{p,q\}=1}$일 때

${\displaystyle \gcd\{ap+bq,cp+dq\}=1}$

이게 된다. 이 작용은 추이적 작용이다. 즉, 임의의 ${\displaystyle (p,q),(p',q')\in X}$에 대하여, 항상 ${\displaystyle M\cdot (p,q)=(p',q')}$인 ${\displaystyle M\in \operatorname {SL} (2;\mathbb {Z} )}$이 존재한다.

이제, 다음과 같은 전사 함수를 생각하자.

${\displaystyle X\to \mathbb {P} _{\mathbb {Q} }^{1}=\mathbb {Q} \sqcup \{\infty \}}$

${\displaystyle (p,q)\mapsto {\frac {p}{q}}\qquad (q\neq 0)}$

${\displaystyle (\pm 1,0)\mapsto \infty }$

즉, ${\displaystyle (p,q)}$를 약분 불가능 분수 ${\displaystyle p/q}$로 간주하자. 물론 ${\displaystyle p/q=(-p)/(-q)}$이므로, 이는 ${\displaystyle \operatorname {SL} (2;\mathbb {Z} )}$의 몫군 ${\displaystyle \operatorname {PSL} (2;\mathbb {Z} )}$의, 유리수 사영 직선 위의 작용을 정의한다. 이 작용 역시 따라서 추이적 작용이다.

이 작용 아래 ${\displaystyle {\mathsf {S}}}$와 ${\displaystyle {\mathsf {T}}}$의 작용은 다음과 같다.

${\displaystyle {\mathsf {S}}\cdot {\frac {p}{q}}=-{\frac {q}{p}}}$

${\displaystyle {\mathsf {T}}\cdot {\frac {p}{q}}={\frac {p+q}{q}}={\frac {p}{q}}+1}$

이 작용은 모듈러 군의, 복소수 상반평면 위의 작용을 유리수로 제한한 것이다.

꼬임군과의 관계

모듈러 군의 보편 중심 확대는 3차 꼬임군 ${\displaystyle \operatorname {Braid} (3)}$이다. 즉, 다음과 같은 가환 그림이 존재한다.

${\displaystyle {\begin{matrix}\operatorname {Cyc} (\infty )&\hookrightarrow &\operatorname {Braid} (3)&\twoheadrightarrow &\operatorname {PSL} (2;\mathbb {Z} )\\\|&&\downarrow &&\downarrow \\\operatorname {Cyc} (\infty )&\hookrightarrow &{\overline {\operatorname {SL} (2;\mathbb {R} )}}&\twoheadrightarrow &\operatorname {PSL} (2;\mathbb {R} )\end{matrix}}}$

여기서 ${\displaystyle {\overline {\operatorname {SL} (2;\mathbb {R} )}}}$는 2차원 실수 특수선형군의 범피복군이며, ${\displaystyle \operatorname {Cyc} (\infty )}$는 무한 순환군(정수의 덧셈군)이다.

합동 부분군

모듈러 군은 합동 부분군(영어: congruence subgroup)이라는 일련의 부분군들을 가진다. 일반적으로, 합동 부분군은 (아래에 정의된) ${\displaystyle \Gamma (N)}$을 부분군으로 가지는 ${\displaystyle \Gamma }$의 부분군 ${\displaystyle \Gamma (N)\subset G\subset \Gamma (1)}$이다. 이 경우, 이러한 최소 ${\displaystyle N}$을 합동 부분군 ${\displaystyle G}$의 준위(영어: level 레벨^[*], 독일어: Stufe 슈튜페^[*])라고 한다.

흔히 쓰이는 합동 부분군으로는 ${\displaystyle \Gamma (N)}$, ${\displaystyle \Gamma _{0}(N)}$, ${\displaystyle \Gamma _{1}(N)}$이 있다. 이들은 다음과 같은 관계를 가진다.

${\displaystyle \Gamma (N)\subset \Gamma _{1}(N)\subset \Gamma _{0}(N)}$

모듈러 군 Γ(N)

모듈러 군 ${\displaystyle \Gamma }$는 주합동 부분군(主合同部分群, 영어: principal congruence subgroup)이라는 중요한 부분군들을 가진다. ${\displaystyle N\geq 2}$가 양의 정수라고 하면, 2×2 정수 행렬의 모든 수를 ${\displaystyle N}$에 대한 동치류들로 치환하는 다음과 같은 군 준동형이 존재한다.

${\displaystyle \Gamma =\operatorname {PSL} (2;\mathbb {Z} )\to \operatorname {PSL} (2;\mathbb {Z} /N\mathbb {Z} )}$

이 군 준동형의 핵을 레벨 N의 주합동 부분군 ${\displaystyle \Gamma (N)}$이라고 한다. 즉, 다음과 같은 짧은 완전열이 있다.

${\displaystyle 1\to \Gamma (N)\hookrightarrow \Gamma \twoheadrightarrow \operatorname {PSL} (2;\mathbb {Z} /N\mathbb {Z} )\to 1}$

구체적으로, ${\displaystyle \Gamma (N)}$은 다음과 같은 꼴의 행렬들로 이루어진다. 행렬

${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$

에 대하여,

${\displaystyle a\equiv d\equiv \pm 1{\pmod {N}}}$

${\displaystyle b\equiv c\equiv 0{\pmod {N}}}$

특히, ${\displaystyle \Gamma (2)=\Lambda }$는 Λ 모듈러 군(영어: modular group Λ)라고 불린다. 이 경우 ${\displaystyle \operatorname {SL} (2;\mathbb {Z} /2)\cong \operatorname {Sym} (3)}$은 3차 순환군이므로 크기가 6이다. 즉, ${\displaystyle \Lambda }$는 지표가 6인 부분군이다.

모듈러 군 Γ₁(N)

모듈러 군 Γ₁(N)은 ${\displaystyle \Gamma }$의 부분군이며, 다음과 같은 꼴의 원소를 포함한다. 행렬

${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$

에 대하여,

${\displaystyle a\equiv d\cong 1}$

${\displaystyle c\equiv 0{\pmod {N}}}$

모듈러 군 Γ₀(N)

모듈러 군 Γ₀(N)은 ${\displaystyle \Gamma }$의 부분군이며, 다음과 같은 꼴의 원소를 포함한다. 행렬

${\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$

에 대하여,

${\displaystyle c\equiv 0{\pmod {N}}}$

즉, 위와 같이 ${\displaystyle \Gamma \to \operatorname {PSL} (2;\mathbb {Z} /N\mathbb {Z} )}$와 같은 군 준동형에서, 상이 상삼각행렬인 원소들이다. ${\displaystyle \Gamma (N)}$은 ${\displaystyle \Gamma _{0}(N)}$의 부분군이다.

참고 문헌

• Apostol, Tom M. (1990). 《Modular functions and Dirichlet series in number theory》. Graduate Texts in Mathematics (영어) 41 2판. Springer. doi:10.1007/978-1-4612-0999-7. ISBN 978-0-387-97127-8. ISSN 0072-5285. Zbl 0697.10023. CS1 관리 - 추가 문구 (링크)

외부 링크

• Panchishkin, A. A. (2001). “Modular group”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. ISBN 978-1-55608-010-4.
• Weisstein, Eric Wolfgang. “Modular Group Gamma”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• Weisstein, Eric Wolfgang. “Modular Group Lambda”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• Weisstein, Eric Wolfgang. “Modular Group Gamma_0”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• 이철희. “모듈라 군(modular group)”. 《수학노트》.

같이 보기

• 푹스 군
• 모듈러 형식
• 2차원 실수 특수선형군
• 뫼비우스 변환