Neeuklidinė geometrija

Neeuklidinė geometrija – plačiąja prasme, bet kokia geometrija, kuri skiriasi nuo Euklidinės (parabolinės) geometrijos.^[1] Tačiau tradiciškai terminas „neeuklidinė geometrija“ yra labiau taikomas siauresne prasme ir apima tik dvi geometrines sistemas: Lobačevskio hiperbolinę geometriją ir į ją panašią sferinę geometriją arba (Rymano geometriją ir elipsinę geometriją).

Trikampis elipsinėje, hiperbolinėje ir euklidinėje geometrijoje.

Neeuklidinėse geometrijose kreivės yra naudojamos kaip tiesės Euklidinėje geometrijoje. Nulinis kreivumas atitinka Euklidinę geometriją, teigiamas kreivumas - sferinę, Riemanno arba elipsinę geometriją, o neigiamas kreivumas – Lobačevskio geometriją.

Trikampiai neeuklidinėse geometrijose

Sferos paviršius nėra Euklidinis ir dėl to trikampio kampų suma yra didesnė nei 180°. Nors lokaliai Euklido geometrijos dėsniai yra tinkami, pavyzdžiui, mažame trikampyje žemės paviršiuje trikampio kampų suma yra beveik lygi 180°.

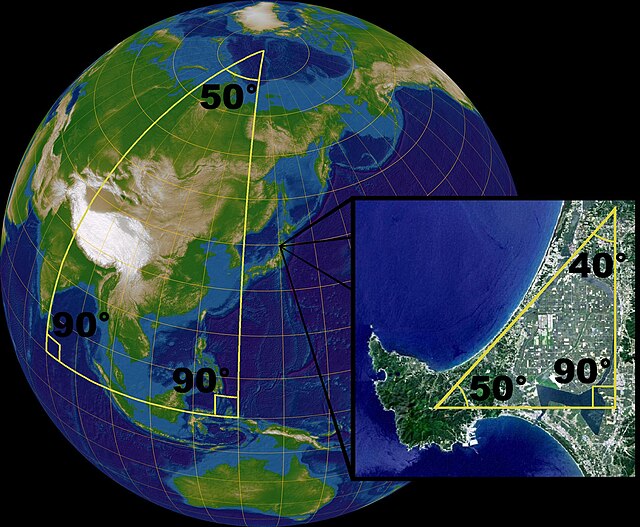
Neeuklidinėse geometrijose kaip ir Euklidinėse galima nubrėžti trikampius, tačiau skiriasi jų savybės. Neeuklidinėse geometrijose nėra nei stačių kampų, nei nevienodų panašių trikampių. Trikampio vidinių kampų suma yra lygi 180° tik Euklidinėje geometrijoje, bet ne kitose.