ആയാസം

ഒരു വസ്തുവിന്റെ ആകാരത്തിൽ വ്യത്യസം ഉണ്ടാക്കാൻ തക്കവണ്ണം പ്രതിമാത്ര വിസ്തീർണത്തത്തിൽ അനുഭവപ്പെടുന്ന ബലമാണ് ആയാസം (Stress).^[2]

Figure 1.1 ബലമേറ്റിയ വിരൂപണക്ഷമമായ ഒരു വസ്തുവിനെ ഒരു തുടർമാനമായി(continuum) കണക്കാക്കുന്നു.

Figure 1.2 അക്ഷീയമായി ബലമേറ്റിയ സ്ഫടികാകാരമായ ദണ്ഡിലെ അക്ഷീയ ആയാസം (Axial stress)

Figure 1.3 സ്ഫടികകാര ബാറിലെ അഭിലംബ ആയാസം. പരിച്ഛേദതലത്തിലെ ആയാസം ഏകതാനമാകണമെന്നില്ല. എന്നിരുന്നാലും ശരാശരി അഭിലംബ ആയാസം കണക്കാക്കാൻ ${\displaystyle \sigma _{\mathrm {avg} }\,\!}$ ഉപയോഗിക്കാം.

Figure 1.4 സ്ഫടികാകാര ബാറിലെ അപരൂപണ ആയാസം. പരിച്ഛേദതലത്തിലെ ആയാസം ഏകതാനമാകണമെന്നില്ല. എന്നാലും ശരാശരി അപരൂപണ ആയാസം ${\displaystyle \tau _{\mathrm {avg} }\,\!}$ എന്ന് കണക്കാക്കാം.^[1]

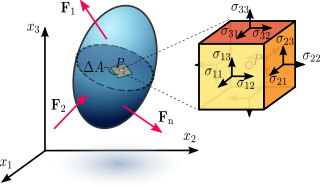
പദാർത്ഥകണികകൾ തമ്മിലുളള ആന്തരികബലത്തിന്റെ അളവാണ് ആയാസം.^[2] ഈ ആന്തരികബലങ്ങൾ ആ വസ്തുവിൽ പ്രയോഗിച്ച ബാഹ്യബലത്തിന്റെ പ്രതിബലമാണ്. ഈ പ്രതിബലം വസ്തുവിനെ വിഭജിക്കാനോ, സമ്മർദ്ദിക്കാനോ, നിരക്കിനീക്കാനോ കാരണമായേക്കാവുന്നതാണ്.^[2] ബാഹ്യബലങ്ങൾ പ്രതലബലങ്ങളോ (surface force) കായബലങ്ങളോ (body force) ആകാം. പദാർത്ഥത്തിലെ ഒരു സാങ്കല്പിക തലത്തിനിടയിലൂടെ ഒരു കണം തൊട്ടടുത്ത കണത്തിന്മേൽ ചെലുത്തുന്ന ശരാശരി ബലം പ്രതി വിസ്തീർണം ആണ് ആയാസം. The formula for uniaxial normal stress is:

${\displaystyle {\sigma }={\frac {F}{A}}}$

ഇതിൽ σ എന്നാൽ ആയാസം, F എന്നാൽ ബലം, A എന്നാൽ പ്രതലവിസ്തീർണ്ണം.

സാർവ്വദേശീയ ഏകകവ്യവസ്ഥ (SI unit)പ്രകാരം, ബലത്തെ ന്യൂട്ടനിലും വിസ്തീർണത്തെ ചതുശ്രമീറ്ററിലും ആണ് അളക്കുന്നത്. ഇതിൽ നിന്നും, ആയാസത്തിന്റെ ഏകകം ന്യൂട്ടൺ പ്രതി ച.മീറ്റർ (N/m²) ആണെന്നു കാണാം. ആയാസത്തിന്റെ എസ് ഐ ഏകകത്തെ പാസ്കൽ (pascal) എന്നാണ് അറിയപ്പെടുന്നത്. 1 pascal (symbol Pa) is equal to 1 N/m² ഇംപീരിയൽ ഏകകവ്യവസ്ഥയിൽ ഇത് പൗണ്ട്ബലം പ്രതി ചതുരശ്രഇഞ്ച് ("psi")ആയി ആണ് അളക്കപ്പെടുന്നത്. ആയാസത്തിന്റെ മാനവും (dimension) മർദ്ദത്തിന്റെ മാനവും ഒന്നുതന്നെയാണ്.

തുടർമാനബലതന്ത്രത്തിൽ (continuum mechanics) ബലമേറ്റപ്പെട്ട (loaded) വിരൂപണക്ഷമമായ (deformable) ഒരു വസ്തു ഒരു തുടർമാനം (continuum) പോലെ പെരുമാറും. അതായത്, ആന്തരികബലങ്ങൾ ആ വസ്തുവിന്റെ വ്യാപ്തത്തിലുടനീളം തുടർച്ചയായി വിതരണം ചെയ്യപ്പെടും. ഈ ബലങ്ങൾ ആ വസ്തുവിന്റെ വിരൂപണത്തിന് കാരണമാകുന്നു. വസ്തുവിന്റ പ്രബലത (Strength) പര്യാപ്തമല്ലെങ്കിൽ അത് സ്ഥിരമായ ആകൃതിമാറ്റത്തിനോ ഘടനാമാറ്റത്തിനോ വിധേയമായേക്കാം.

1. Walter D. Pilkey, Orrin H. Pilkey (1974). Mechanics of solids. p. 292.
2. Daintith, John, ed. (2005). A Dictionary of Physics (Fifth ed.). Oxford University Press. p. 509. ISBN 978-0-19-280628-4.