Bulatan

Dalam bidang matematik, bulatan ditakrifkan sebagai lokus bagi titik yang bergerak dari satu titik tetap pada jarak malar. Jarak tersebut dikenali sebagai jejari (lazimnya ditandakan dengan simbol j atau r), manakala titik tetap tersebut dikenali sebagai titik tengah atau pusat(lazimnya ditandakan dengan simbol O atau θ).

Bulatan; O ialah titik tengah, r ialah jejari, P ialah suatu titik pada lilitan bulatan.

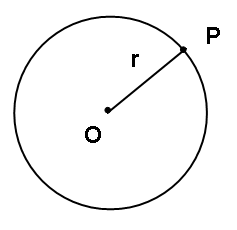
Dua kali ganda jejari dikenali sebagai diameter. Diameter boleh juga ditakrifkan sebagai tembereng garis yang melalui titik tengah, dengan kedua-dua hujungnya menyentuh hujung bulatan.

Ciri-ciri metrik

Lilitan

Perimeter bagi bulatan juga dikenali sebagai lilitan atau ukur lilit. Jika panjang jejari diberikan, panjang lilitan p bagi suatu bulatan boleh dihitung dengan menggunakan rumus berikut:

${\displaystyle p=2\pi {j}\!}$

atau, jika diameter diberikan,

${\displaystyle p=\pi {d}\!}$

di mana j ialah jejari, d ialah diameter dan π ialah pi (π ≈ 3.142...).

Luas

Keluasan bulatan boleh dihitung dengan menggunakan rumus berikut:

${\displaystyle \mathrm {keluasan} =\pi j^{2}\,}$

atau, jika diameter diberikan,

${\displaystyle \mathrm {keluasan} ={\frac {\pi d^{2}}{4}}\approx 0{.}7854d^{2}}$

Persamaan

Persamaan Cartesian

Sebuah segi tiga bersudut tepat di dalam sebuah bulatan pada satah Cartesian.

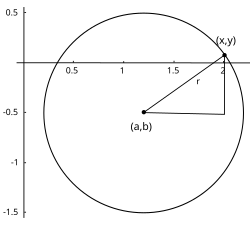
Dalam satu satah Cartesian, sebuah bulatan dengan pusat pada titik (a,b) dengan jejari, j memiliki persamaan seperti di bawah:

${\displaystyle (x-a)^{2}+(y-b)^{2}=j^{2}.}$

Persamaan ini menuruti Teorem Pythagoras yang diaplikasikan pada mana-mana titik di bulatan. Dalam hal ini, jejari bulatan dianggap sebagai hipotenus bagi sebuah segi tiga bersudut tepat dengan panjang sisi-sisi lain ialah |x − a| dan |y − b|.

Sekiranya pusat bulatan berada di titik asalan, (0,0), persamaan boleh diringkaskan menjadi ${\displaystyle x^{2}+y^{2}=j^{2}.}$

Lihat juga

• Elips
• Pi
• Sfera

Pautan luar

• Kategori berkenaan Bulatan di Wikimedia Commons
• Takrifan kamus bulatan di Wikikamus