ဧရိယာ

ဧရိယာသည် ပမာဏတစ်ခုဖြစ်ပြီး နှစ်ဖက်မြင်ပုံ ( two-dimensional figure) သို့ ပုံသဏ္ဌာန်၊ သို့ ပြင်ညီရှိ planar lamina တို့၏ ပမာဏကို ဖော်ပြသည်။

The combined area of these three shapes is approximately 15.57 squares.

ပုံတစ်ခု၏ ဧရိယာကို တိကျသောအရွယ်အစားရှိသည် စတုရန်းနှင့် နှိုင်းယှဉ်၍ တိုင်းတာနိုင်သည်။^[၁] အပြည်ပြည်ဆိုင်ရာယူနစ်စနစ် (SI) တွင် ဧရိယာ၏ စံယူနစ်မှာ စတုရန်းမီတာ (m² ဟုရေးရသည်) ဖြစ်ပြီး ထိုစတုရန်း၏ဧရိယာကို ရရှိစေသော အနားတစ်ခုသည် ၁ မီတာ ရှည်သည်။^[၂] ၃ စတုရန်းမီတာ ဧရိယာရှိသော ပုံသဏ္ဍန်တစ်ခုသည် ထိုကဲ့သို့ပင် ၃ မီတာရှည်သော အနားရှိသည့် စတုရန်း၏ ဧရိယာနှင့် တူညီသောဧရိယာရှိမည်ဖြစ်သည်။ သင်္ချာပညာရပ်တွင် unit square ဆိုသည်မှာ ဧရိယာသည် ၁ ရှိရမည်ဖြစ်ပြီး အခြားသောပုံသဏ္ဌာန်များနှင့် မျက်နှာပြင်များသည် dimensionless real number များဖြစ်ကြသည်။

တြိဂံ၊ ထောင့်မှန်စတုဂံနှင့် စက်ဝိုင်းကဲ့သို့.ရိုးရှင်းသောပုံများအတွက် ဧရိယာရှာရန် ဆိုင်ရာပုံသေနည်းများကို သိရှိကြပြီးဖြစ်သည်။ ထိုပုံသေနည်းများကို အသုံးပြု၍ မည်သည့် ဗဟုဂံအတွက်မဆို ဧရိယာရှာရန် ဗဟုဂံအား တြိဂံများအဖြစ်သို့ ပိုင်းဖြတ်ခြင်းဖြင့် ရှာနိုင်သည်။^[၃] မျဉ်းကွေးများဖြင့် ပိုင်းခြားထားသောပုံများအတွက် ကဲကုလပ်ဖြင့် ထိုဧရိယာများကို တွက်ထုတ်ရန် လိုအပ်ပေသည်။ Indeed, အမှန်တော့ ထိုကဲ့သို့ တွက်ချက်နိုင်ခဲ့ခြင်းပင်လျှင် ကဲကုလပ်ဘာသာရပ်သမိုင်းအတွက်  တိုးတက်ပြောင်းလဲမှုကြီးဖြစ်ခဲ့သည်။^[၄]

ယူနစ်များ

A square metre quadrat made of PVC pipe.

အလျားယူနစ်တိုင်းတွင် ဆိုင်ရာ ဧရိယာ၏ ယူနစ်များရှိကြသည်။  ထိုကြောင့် ဧရိယာကို စတုရန်းမီတာ (m²)၊ စတုရန်းစင်တီမီတာ (cm²)၊ စတုရန်းမီလီမီတာ (mm²)၊ စတုရန်းကီလိုမီတာ (km²)၊ စတုရန်းပေ (ft²)၊ စတုရန်းကိုက် (yd²)၊ စတုရန်းမိုင် (mi²) အစရှိသဖြင့်တို့နှင့် တိုင်းတာနိုင်သည်။ အက္ခရာသင်္ချာနည်းအရ ထိုယူနစ်များသည် သက်ဆိုင်ရာ အလျားယူနစ်များ၏ နှစ်ထပ်ကိန်းများအဖြစ် မှတ်ယူနိုင်သည်။

ဧရိယာ၏ SI ယူနစ်သည် စတုရန်းမီတာဖြစ်သော်ကြောင့် SI မှ ဆင်းသက်လာသော ယူနစ်ဟု မှတ်ယူနိုင်သည်။

ယူနစ်များပြောင်းလဲခြင်း

Although there are 10 mm in 1 cm, there are 100 mm² in 1 cm².

အလျားနှင့် အနံ  ၁ မီတာရှိသော စတုန်းရန်း၏ဧရိယာကို တွက်ချက်မည်ဆိုလျှင်:

၁ မီတာ x ၁ မီတာ = ၁ စတုရန်းမီတာ (m2)

ထို့ကြောင့် နောက်ထပ် အနားမတူညီသော စတုရန်း၏ ဧရိယာကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်:

၃ မီတာ x ၂ မီတာ = ၆ စတုရန်းမီတာ (m²)

သို့ပေမယ် ဒါဟာ ၆ မီလီယံ စတုရန်းမီလီမီတာနှင့် ညီမျှမှာ ဖြစ်သည်။ အောက်တွင်ဖော်ပြထားသည်တို့အား ဆက်လက်ကြည့်ရှုကြည့်ပါ-

• ၁ စတုရန်း ကီလိုမီတာ = ၁,၀၀၀,၀၀၀ စတုရန်းမီတာ
• ၁ စတုရန်း မီတာ = ၁၀,၀၀၀ စင်တီမီတာစတုရန်း= ၁,၀၀၀,၀၀၀ စတုရန်း
• ၁ စတုရန်း စင်တီမီတာ = ၁၀၀ စတုရန်း မီလီမီတာ

မက်ထရစ်စနစ်မဟုတ်သော ယူနစ်များ

မက်ထရစ်စနစ်မဟုတ်သော ယူနစ်များတွင် စတုရန်းယူနစ်နှစ်ခုအကြားပြောင်းလဲခြင်းသည် သင့်လျော်သော အလျားယူနှစ်များအကြား နှစ်ထပ်ကိန်းပြောင်းလဲခြင်းဖြစ်သည်။

၁ ပေ = ၁၂ လက်မ

စတုရန်းပေနှင့် စတုရန်းလက်မအကြား ဆက်နွယ်ချက်မှာ အောက်ပါအတိုင်းဖြစ်သည်။

၁ စတုရန်းပေ = ၁၄၄ စတုရန်းလက်မ

အဲဒီ၌ ၁၄၄ = ၁၂^၂ = ၁၂ × ၁၂။ ထိုအတူပင်:

• ၁ စတုရန်းကိုက် = ၉ စတုရန်းပေ
• ၁ စတုရန်းမိုင် = ၃,၀၉၇,၆၀၀ စတုရန်းကိုက် = ၂၇,၈၇၈,၄၀၀ စတုရန်းပေ
  

ဖြည့်စွက်ချက်အနေဖြင့် အောက်ဖော်ပြပါ ပြောင်းလဲခြင်းများလည်း ပါဝင်ပေသည်:

• ၁ စတုရန်းလက်မ = 6.4516 စတုရန်းစင်တီမီတာ
• ၁ စတုရန်းပေ = 0.09290304 စတုရန်းမီတာ
• ၁ စတုရန်းကိုက် = 0.83612736 စတုရန်းမီတာ
• ၁ စတုရန်းမိုင် = 2.589988110336 စတုရန်းကီလိုမီတာ

သမိုင်းကြောင်း

စက်ဝိုင်းဧရိယာ

တြိဂံ၏ဧရိယာ

ဟီးရိုး(Heron (or Hero) of Alexandria)သည် တြိဂံများကို ၎င်းတို့၏ အနားများအရ ရှာဖွေသော ဧရိယာရှာရန် ပုံသေနည်းဖြစ်သည့် Heron's formula ကို တွေ့ရှိခဲ့ပြီး ထိုသက်သေပြချက်ကို ၆၀ ရာစုပတ်ဝန်းကျင်တွင် ရေးသားခဲ့သော ၎င်း၏ စာအုပ်ဖြစ်သည့် Metrica တွင် တွေ့နိုင်သည်။ အာခီမီးဒီးစ်သည် ထိုပုံသေနည်းကို နှစ်ရာစုကျော်ကတည်းက ဖော်ပြပြီးဖြစ်သည်ဟုလည်းဆိုသည်။^[၅] Metrica သည် ရှေးခေတ်က တွေ့ရှိခဲ့သော သင်္ချာဆိုင်ရာ အသိဗဟုသုတများကို စုစည်းထားခြင်းဖြစ်ပြီး ထိုပုံသေနည်းသည် ရည်ညွှန်းစာအုပ်ထက် အလျင်ဦးစွာ ပေါ်ထွက်ခဲ့သည်မှာလည်း ဖြစ်နိုင်သည်။^[၆]

Classical age၊ ၄၉၉ ခုနှစ်တွင် အိန္ဒိယလူမျိုး နက္ခတ္တပညာရှင်နှင့် သင်္ချာပညာရှင်ဖြစ်သူ Aryabhata သည် တြိဂံ၏ ဧရိယာကို ၎င်း၏ အခြေအနားတစ်ဝက်နှင့် အမြင့်မြှောက်ခြင်းဖြစ်သည်ဟု Aryabhatiya (section 2.6) တွင် ဖော်ပြခဲ့သည်။

Heron ၏ ပုံသေနည်းနှင့်တူညီသော ပုံသေနည်းကို တရုတ်၌လည်း ဆက်စပ်ခြင်းမရှိပဲ တွေ့ရှိခဲ့သည်။ ၎င်းပုံသေနည်းကို Qin Jiushao ရေးသားသော" Mathematical Treatise in Nine Sections" (ရိုးရှင်းတရုတ်: 数书九章; ရိုးရာတရုတ်: 數書九章; ပင်ယင်: Shùshū Jiǔzhāng; Wade–Giles: Shushu Chiuchang) တွင်ဖော်ပြခဲ့သည်။

စတုဂံဧရိယာ

၇ ရာစုတွင် ဗြဟ္မပုတ္တရ(Brahmagupta)သည် ယခုအခါတွင် ဗြဟ္မပုတ္တရပုံသေနည်း(Brahmagupta's formula)ဟုသိရှိကြသည့် စက်ဝိုင်းအတွင်း ရေးဆွဲထားသော စတုဂံများ(cyclic quadrilateral)၏ ဧရိယာကို ရှာဖွေနိုင်မည့်ပုံသေနည်းကို ဖော်ထုတ်ခဲ့သည်။ ၁၈၄၂ ခုနှစ်တွင် ဂျာမန်သင်္ချာပညာရှင်များဖြစ်ကြသော Carl Anton Bretschneider နှင့် Karl Georg Christian von Staudt တို့သည် မည်သို့သော စတုဂံများ၏ ဧရိယာကိုမဆို ရှာဖွေနိုင်မည့် ပုံသေနည်းကို သီးခြားစီ တွေ့ရှိခဲ့သည်။ နောင်တွင် ၎င်းပုံသေနည်းကို Bretschneider's formula ဟု လူသိများလာသည်။

ယေဘုယျ ဗဟုဂံ ဧရိယာ

၁၇ ရာစုတွင် ရနေး ဒေးကာ့၏ ကာတေးရှန်းကိုဩဒိနိတ်(Cartesian coordinates) ပေါ်ထွန်းလာသောအခါ ၁၉ ရာစု၌ ဂေါက်၏ ထိပ်စွန်းများ(vertex)၏ တည်နေရာ သတ်မှတ်နိုင်ခြင်းနှင့်အတူ မည်သို့သော ဗဟုဂံမဆို ဧရိယာရှာဖွေနိုင်မည့် surveyor's formula သည်လည်း ဖွံဖြိုးလာသည်။

ဧရိယာပုံသေနည်းများ

ဗဟုဂံ

For a non-self-intersecting (simple) polygon, the Cartesian coordinates ${\displaystyle (x_{i},y_{i})}$ (i=0, 1, ..., n-1) of whose n vertices are known, the area is given by the surveyor's formula:^[၇]

${\displaystyle A={\frac {1}{2}}|\sum _{i=0}^{n-1}(x_{i}y_{i+1}-x_{i+1}y_{i})|,}$

where when i=n-1, then i+1 is expressed as modulus n and so refers to 0.

ထောင့်မှန်စတုဂံ

ဖော်ပြပါထောင့်မှန်စတုဂံ၏ ဧရိယာသည် lw ဖြစ်သည်။

အခြေခံအကျဆုံး ဧရိယာပုံသေနည်းမှာ ထောင့်မှန်စတုဂံ၏ ဧရိယာပုံသေနည်းဖြစ်သည်။ အလျား l နှင့် အနံ w ပေးထားသော ထောင့်မှန်စတုဂံ၏ ဧရိယာအား တွက်ရန်ပုံသေနည်းမှာ:^[၁][၈]

A = lw (ထောင့်မှန်စတုဂံ)

ဆိုလိုသည်မှာ ထောင်မှန်စတုဂံ၏ ဧရိယာသည် အလျားနှင့် အနံမြှောက်ခြင်းဖြစ်သည်။ သီးသန့်အခြေအနေဖြစ်သည့်  l = w ဖြစ်သော စတုရန်းတို့တွင် ဘေးအနား s ရှိသော စတုရန်း၏ ဧရိယာသည် ဖော်ပြပါပုံသေနည်းအတိုင်း ဖြစ်သည်:^[၉]

A = s² (စတုရန်း)

ထောင့်မှန်စတုဂံ၏ ဧရိယာပုံသေနည်းသည် ဧရိယာ၏ အခြေခံဂုဏ်သတ္တိများမှ ဆင်းသက်လာခဲ့ခြင်းဖြစ်ပြီး ၎င်းကို ဖွင့်ဆိုချက် သို့ စစ်မှန်သော အမှန်တရားအဖြစ် ယူကြသည်။ အခြားအနေဖြင့်လည်း အကယ်၍ ဂျီဩမေတြီသာ ဂဏန်းသင်္ချာထက် စောစီးစွာ တိုးတက်ဖွံ့ဖြိုးခဲ့မည်ဆိုပါက ဤပုံသေနည်းကို ကိန်းစစ်များ၏ မြှောက်ခြင်းကို ဖော်ပြရာတွင် သုံးနိုင်ပေလိမ်မည်။

တူညီသောဧရိယာရှိသော ပုံများ

ခွဲခြမ်းစိတ်ဖြာလေ့လာခြင်း၊ အနားပြိုင်စတုဂံနှင့် တြိဂံများ

အခြားရိုးရှင်းသော ဧရိယာ၏ ပုံသေနည်းများသည် ခွဲခြမ်းစိတ်ဖြာလေ့လာနည်းမှ ရရှိလာသည်။ ထိုအထဲတွင် ပုံများအား အစိတ်အပိုင်းများအဖြစ် ဖြတ်ထောက်ပြီး ထိုအစိတ်အပိုင်းများ၏ ဧရိယာကို မူလပုံ၏ ဧရိယာသို့ ပေါင်းထည့်ခြင်းတို့ ပါဝင်သည်။

ဥပမာအားဖြင့် မည်သည့် အနားပြိုင်စတုဂံကိုဖြစ်စေ တြာပီဇီယံ(အနားမပြိုင်စတုဂံ)နှင့် ထောင့်မှန်တြိဂံအဖြစ် ဘယ်ဘက်တွင်ပြသထားသောပုံကဲ့သို့ စိတ်ပိုင်းနိုင်သည်။ တြိဂံကို အနားမပြိုင်စတုဂံ၏ တခြားသောဘက်သို့ထားလိုက်မည်ဆိုပါက ထောင့်မှန်စတုဂံပုံကို ရရှိလာမည်ဖြစ်သည်။ ထိုသည်ကို ကြည့်ခြင်းအားဖြင့် အနားပြိုင်စတုဂံ၏ ဧရိယာသည် ထောင်မှန်စတုဂံ၏ ဧရိယာနှင့် အတူတူပင်ဖြစ်နေသည်:

A = bh  (အနားပြိုင်စတုဂံ)

တူညီသော တြိဂံများ

ထိုအနားပြိုင်စတုဂံကိုပင် ၎င်း၏ထောင့်ဖြတ်မျဉ်းအတိုင်း ဖြတ်လိုက်မည်ဆိုပါက ညာဘက်တွင်ပြသထားသော ပုံအတိုင်း ထပ်တူညီသော တြိဂံနှစ်ခုရရှိမည်ဖြစ်သည်။ ထိုသည်ကို ကြည့်ခြင်းအားဖြင့် တြိဂံတစ်ခုစီ၏ဧရိယာသည် ထိုအနားပြိုင်စတုဂံ၏ ဧရိယာတစ်ဝက်စီဖြစ်နေမည်ဖြစ်သည်:

${\displaystyle A={\frac {1}{2}}bh}$  (တြိဂံ)

ထိုကဲ့သို့သော အကြောင်းပြချက်များကို အသုံးပြု၍ အနားမညီစတုဂံ^[၁၀]နှင့် ပိုမို ရှုပ်ထွေးသော ဗဟုဂံတို့၏ ဧရိယာများကို ရှာဖွေနိုင်သည်။^[၁၁]

မျဉ်းကွေးများပါဝင်သော ပုံများ၏ ဧရိရှာကို ရှာဖွေခြင်း

စက်ဝိုင်း

A circle can be divided into sectors which rearrange to form an approximate parallelogram.

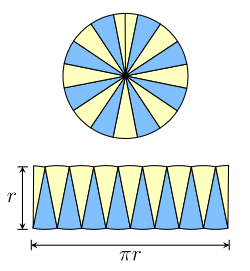
စက်ဝိုင်းအတွက် ဧရိယာရှာရန်ပုံသေနည်း (သေချာစွာ ပြောရမည်ဆိုလျှင် စက်ဝိုင်းတစ်ခုဖြင့် ပတ်ရံထားသော ဧရိယာ သို့ အပြားတစ်ခု၏ ဧရိယာ)သည် အနားပြိုင်စတုဂံတို့၏ ဧရိယာကို ရှာဖွေနည်းကဲ့သို့ တူညီသောနည်းကို အခြေခံထားခြင်းဖြစ်သည်။ ပေးထားသော စက်ဝိုင်း၏ အချင်းဝက်သည် r ဖြစ်မည်ဆိုပါက ထိုစက်ဝိုင်းကို စက်ဝိုင်းစိတ်များအဖြစ် ညာဘက်တွင်ပြသထားသောပုံအတိုင်း ခွဲစိတ်နိုင်မည်ဖြစ်သည်။ စက်ဝိုင်းစိတ်တိုင်းတစ်ခုစီသည် တြိဂံပုံနီးနီးဖြစ်နေပြီး ထိုစက်ဝိုင်းစိတ်များကို ပြန်လည်နေကျချစီလိုက်မည်ဆိုပါက အနာပြိုင်စတုဂံပုံနှင့် တူလုနီးပါး ရရှိလာမည်ဖြစ်သည်။ ထိုအနားပြိုင်စတုဂံ၏ အမြင့်သည် r ဖြစ်ပြီး အကျယ်သည် စက်ဝန်းမျဉ်း၏ တဝက် သို့ πr ဖြစ်သည်။  ထိုကြောင့် စက်ဝိုင်း၏ စုစုပေါင်းဧရိယာသည် r × πr, သို့ πr² ဖြစ်သည်:

A = πr²  (စက်ဝိုင်း)

ဤပုံသေနည်းတွင် ခွဲခြမ်းစိတ်ဖြာလေ့လာခြင်းကို အသုံးပြုထားလင့်ကစား ခန့်မှန်းခြေမျှသာရရှိသည် စက်ဝိုင်းကို စက်ဝိုင်းစိတ်များ ပို၍ပို၍ခွဲနိုင်လေလေ မှားနိုင်ချေနည်းနိုင်သမျှ နည်းလေဖြစ်သည်။ အနားပြိုင်စတုဂံနှင့် တူလှနီးပါပုံ၏ ဧရိယာ ကန့်သတ်ချက်သည် စက်ဝိုင်းဧရိယာ  πr² အတိအကျပင်ဖြစ်သည်။

ဤအကြောင်းပြချက်သည် အမှန်စင်စစ် ကဲကုလပ်၏ သဘောသဘာဝကို ရိုးရှင်းစွာ အသုံးချခြင်းပင်ဖြစ်သည်။ ရှေးကာလက စက်ဝိုင်း၏ ဧရိယာရှာဖွေရန် method of exhaustion နည်းကို ထိုနည်းအတိုင်း အသုံးပြုခဲ့ဘူးသည်။ ယခုအခါ ထို method of exhaustion နည်းကို အင်တီဂရယ် ကဲကုလပ်၏ ရှေ့ပြေးအဖြစ် အသိအမှတ်ပြုခဲ့ကြသည်။ ခေတ်မှီနည်းများဖြစ်သော definite integral နည်းကို အသုံးပြု၍ စက်ဝိုင်း၏ ဧရိယာကို အောက်ပါအတိုင်းတွက်ထုတ်နိုင်သည်:

${\displaystyle A\;=\;2\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx\;=\;\pi r^{2}.}$

ဘဲဥပုံ အီလစ်များ

ဘဲဥပုံဖြင့် ပတ်ရံထားသော ဧရိယာအတွက် ပုံသေနည်းမှာ စက်ဝိုင်းပုံသေနည်းနှင့် ဆက်နွယ်နေပြီး semi-major နှင့် semi-minor axes များဖြစ်သည့် x နှင့် y ရှိသော အီလစ်အတွက် ပုံသေနည်းမှာ:^[၁]

${\displaystyle A=\pi xy.}$