Symmetrische groep

In de groepentheorie, een onderdeel van de wiskunde, is de symmetrische groep ${\displaystyle S_{n}}$ van een eindige verzameling ${\displaystyle M}$ met ${\displaystyle n}$ elementen de groep van alle permutaties van ${\displaystyle M}$.^[1] De groepsoperatie is de samenstelling van afbeeldingen. In plaats van ${\displaystyle S_{n}}$ wordt de symmetrische groep van ${\displaystyle M}$ ook wel genoteerd als ${\displaystyle \operatorname {Sym} (M)}$. Aangezien er ${\displaystyle n!}$ permutaties zijn van ${\displaystyle n}$ verschillende elementen, is de orde, het aantal elementen van de symmetrische groep ${\displaystyle S_{n}}$ gelijk aan ${\displaystyle n!}$.

Cayley-graaf van de symmetrische groep ${\displaystyle S_{4}}$
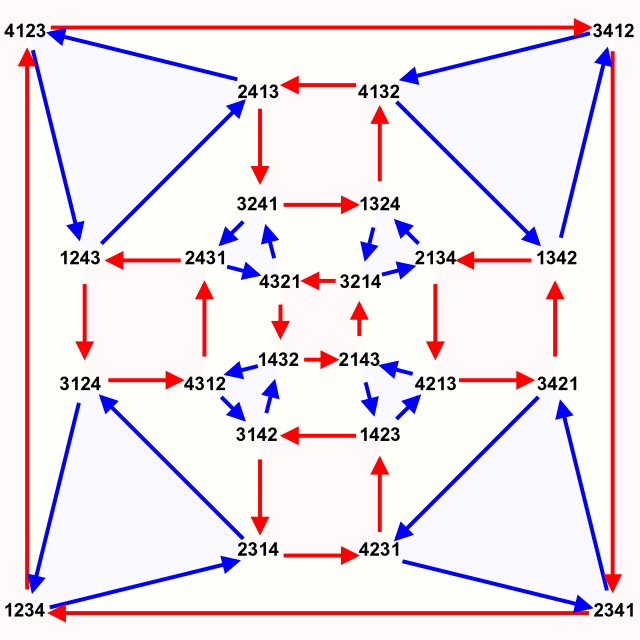
voortbrengers

 2314

 2341

Iedere permutatiegroep van een verzameling met ${\displaystyle n}$ elementen is een ondergroep van ${\displaystyle S_{n}}$.

Voorbeeld

De symmetrische groep ${\displaystyle S_{3}}$ van alle permutaties van een verzameling met drie elementen, voor het gemak de verzameling {1,2,3}, bestaat uit de volgende zes permutaties:

123, 132, 213, 231, 312, 321

In cykelnotatie zijn dat:

(1)(2)(3), (1)(23), (12)(3), (123), (132) en (13)(2) (de eerste is de identiteit)

Het product van 213 en 312 verkrijgt men door de beide permutaties achter elkaar uit te voeren: 213 o 312 = 321. In cykelnotatie: (12)(132) = (13).

Symmetrische groep versus symmetriegroep

Het begrip 'symmetrische groep' moet wel worden onderscheiden van het begrip 'symmetriegroep'. Zo is bijvoorbeeld ${\displaystyle S_{4}}$, met 24 elementen, de symmetrische groep van de verzameling hoekpunten van een vierkant, en de dihedrale groep ${\displaystyle D_{4}}$, met 8 elementen, de symmetriegroep van die verzameling. De overige 16 permutaties zijn geen isometrieën.

O is algebraïsch de symmetrische groep ${\displaystyle S_{4}}$, waarbij de elementen 1-op-1 overeenkomen met de permutaties van de lichaamsdiagonalen van de kubus.^[2]

Voetnoten

1. De notatie ${\displaystyle S_{n}}$ wordt ook gebruikt voor een van de zeven reeksen symmetriegroepen in 3D.
2. Rotation of group of rigid motions of cube is isomorphic to S4