Algorytm Floyda-Warshalla

Algorytm Floyda-Warshalla wykorzystujący metodę programowania dynamicznego algorytm służący do znajdowania najkrótszych ścieżek pomiędzy wszystkimi parami wierzchołków w grafie ważonym^[1]. Graf może zawierać gałęzie zarówno o dodatniej i o ujemnej wadze („długości”), lecz nie może zawierać ujemnych cykli (cykli, w których suma wag krawędzi jest ujemna).

Algorytm Floyda-Warshalla

Rodzaj	problem najkrótszej ścieżki
Struktura danych	graf skierowany
Złożoność
Czasowa	${\displaystyle O(|V|^{3})}$
Pamięciowa	${\displaystyle O(|V|^{2})}$

Opis algorytmu

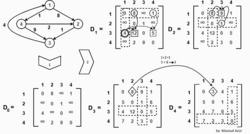
Algorytm Floyda-Warshalla korzysta z tego, że jeśli najkrótsza ścieżka pomiędzy wierzchołkami ${\displaystyle v_{1}}$ i ${\displaystyle v_{2}}$ prowadzi przez wierzchołek ${\displaystyle u,}$ to jest ona połączeniem najkrótszych ścieżek pomiędzy wierzchołkami ${\displaystyle v_{1}}$ i ${\displaystyle u}$ oraz ${\displaystyle u}$ i ${\displaystyle v_{2}.}$ Na początku działania algorytmu inicjowana jest tablica długości najkrótszych ścieżek, tak że dla każdej pary wierzchołków ${\displaystyle (v_{1},v_{2})}$ ich odległość wynosi:

${\displaystyle d[v_{1},\,v_{2}]={\begin{cases}0,&{\mbox{gdy}}\ v_{1}=v_{2}\\w(v_{1},\,v_{2}),&{\mbox{gdy}}\ (v_{1},\,v_{2})\in E\\+\infty ,&{\mbox{gdy}}\ (v_{1},\,v_{2})\notin E\end{cases}}}$

Algorytm jest dynamiczny i w kolejnych krokach włącza do swoich obliczeń ścieżki przechodzące przez kolejne wierzchołki. Tak więc w ${\displaystyle k}$-tym kroku algorytm zajmie się sprawdzaniem dla każdej pary wierzchołków, czy nie da się skrócić (lub utworzyć) ścieżki pomiędzy nimi przechodzącej przez wierzchołek numer ${\displaystyle k}$ (kolejność wierzchołków jest obojętna, ważne tylko, żeby nie zmieniała się w trakcie działania programu). Po wykonaniu ${\displaystyle |V|}$ takich kroków długości najkrótszych ścieżek są już wyliczone.

Wydajność algorytmu

• Złożoność obliczeniowa: ${\displaystyle O(|V|^{3})}$^[1]
• Złożoność pamięciowa: ${\displaystyle O(|V|^{2})}$^[2]

Zapis w pseudokodzie

Dla grafu ${\displaystyle G}$ i funkcji wagowej ${\displaystyle w}$ otrzymamy tablicę ${\displaystyle d[v_{1}][v_{2}]}$ odległości pomiędzy wierzchołkami ${\displaystyle v_{1}}$ i ${\displaystyle v_{2}.}$

Floyd-Warshall(G,w)

dla każdego wierzchołka v1 w V[G] wykonaj
  dla każdego wierzchołka v2 w V[G] wykonaj
    d[v1][v2] = nieskończone
    poprzednik[v1][v2] = niezdefiniowane
  d[v1][v1] = 0
dla każdej krawędzi (v1,v2) w E[G]
  d[v1][v2] = w(v1,v2)
  poprzednik[v1][v2] = v1
dla każdego wierzchołka u w V[G] wykonaj
  dla każdego wierzchołka v1 w V[G] wykonaj
    dla każdego wierzchołka v2 w V[G] wykonaj
      jeżeli d[v1][v2] > d[v1][u] + d[u][v2] to
        d[v1][v2] = d[v1][u] + d[u][v2]
        poprzednik[v1][v2] = poprzednik[u][v2]

Zobacz też

• algorytm Johnsona
• problem najkrótszej ścieżki