Diagram Arganda

Diagram Arganda jest sposobem geometrycznego przedstawienia liczby zespolonej na płaszczyźnie^[1]. Liczbie zespolonej ${\displaystyle x+y{\sqrt {-1}}}$ odpowiada w nim punkt ${\displaystyle (x,y)}$ w kartezjańskim układzie współrzędnych na płaszczyźnie. Początek układu współrzędnych odpowiada liczbie zero, a oś odciętych – zbiorowi liczb rzeczywistych.

Historia

Diagram Arganda został po raz pierwszy zastosowany przez matematyka duńskiego Caspara Wessela w 1797 roku, lecz jego dzieło zostało odkryte dopiero po upływie 100 lat, w 1897 roku, gdy Duńska Akademia Nauk wydała jego francuski przekład^[2]. W roku 1806 Szwajcar Jean-Robert Argand opublikował pracę Próba pewnego sposobu przedstawienia wielkości urojonych w konstrukcjach geometrycznych^[3], w której zinterpretował same liczby i oba działania na nich (dodawanie i mnożenie). Książka Arganda, wydana anonimowo, stała się znana po publikacji jej przez Josepha Gergonne’a w Rocznikach matematyki czystej i stosowanej^[4]. Tamże została opublikowana żywa dyskusja na temat interpretacji wielkości urojonych^[5]. Pierwszym matematykiem, który posługiwał się diagramem we właściwy sposób był Carl Friedrich Gauss w dysertacji z 1799 roku.

Praca Wessela

Wessel nie zajmował się subtelnościami w rodzaju pytań o równość odcinków skierowanych (wektorów) na płaszczyźnie, a dla dodawania i mnożenia sprawdzał tylko poszczególne prawa rachunku. Wektor łączący początek układu współrzędnych z punktem ${\displaystyle (0,1)}$ oznaczał przez ${\displaystyle \varepsilon }$ i znalazł następujące wyniki^[6]:

Jednostki podstawowe Wessela

${\displaystyle \cdot }$	${\displaystyle -1}$	${\displaystyle +1}$	${\displaystyle -\varepsilon }$	${\displaystyle +\varepsilon }$
${\displaystyle -1}$	${\displaystyle +1}$	${\displaystyle -1}$	${\displaystyle +\varepsilon }$	${\displaystyle -\varepsilon }$
${\displaystyle +1}$	${\displaystyle -1}$	${\displaystyle +1}$	${\displaystyle -\varepsilon }$	${\displaystyle +\varepsilon }$
${\displaystyle -\varepsilon }$	${\displaystyle +\varepsilon }$	${\displaystyle -\varepsilon }$	${\displaystyle -1}$	${\displaystyle +1}$
${\displaystyle +\varepsilon }$	${\displaystyle -\varepsilon }$	${\displaystyle +\varepsilon }$	${\displaystyle +1}$	${\displaystyle -1}$

Na tej podstawie wnioskował, że ${\displaystyle \varepsilon ={\sqrt {-1}}.}$ Następnie odcinkowi skierowanemu przyporządkował liczbę zespoloną w postaci trygonometrycznej ${\displaystyle r(\cos v+\varepsilon \sin v).}$ Na tak określonych liczbach zespolonych rozważał wszystkie działania i udowodnił wzór de Moivre’a (również dla wykładnika ułamkowego) oraz rozwiązał wiele zadań o trójkątach sferycznych.

Diagram Arganda – ujęcie formalne

Wystarczy określić mnożenie.

Ponieważ

${\displaystyle (x,y)=x+iy,}$

więc

${\displaystyle (a,0)+(x,y)=a+x+iy=(a+x,y)}$

${\displaystyle (a,0)\cdot (x,y)=a\cdot (x+iy)=ax+iay=(ax,ay),}$

czyli liczbę zespoloną ${\displaystyle (a,0)}$ można identyfikować z liczbą rzeczywistą i wtedy

${\displaystyle (x,y)=(x,0)+(0,y)=x+y(0,1).}$

Zatem ${\displaystyle i=(0,1)}$ i ${\displaystyle (0,1)^{2}=-1.}$

Wtedy

${\displaystyle {\begin{aligned}&(a,b)\cdot (x,y)\\[2px]={}&(a+b(0,1))\cdot (x+y(0,1))\\[2px]={}&ax+ay(0,1)+bx(0,1)+by(0,1)^{2}\\[2px]={}&ax-by+(ay+bx)\cdot (0,1)\\[2px]={}&(ax-by,ay+bx).\end{aligned}}}$

Diagram Arganda w ujęciu H.S.M. Coxetera[7]

Suma liczb zespolonych

Punkty na płaszczyźnie dodaje się tak, jak odpowiadające im wektory wychodzące z początku układu (czyli zera):

${\displaystyle (x,y)+(a,b)=(x+a,y+b).}$

Innymi słowy, aby dodać ${\displaystyle (a,b),}$ stosujemy przesunięcie przekształcające punkt ${\displaystyle (0,0)}$ w punkt ${\displaystyle (a,b).}$

Mnożenie liczby zespolonej przez liczbę całkowitą

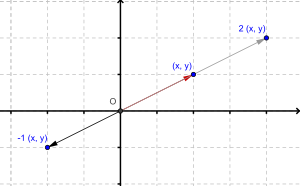
Mnożenie punktu przez liczbę rzeczywistą jest jednokładnością. Na przykład:

${\displaystyle 2(x,y)=(x,y)+(x,y)=(2x,2y)}$

${\displaystyle -1(x,y)=-(x,y)=(-x,-y)}$

${\displaystyle k\cdot (x,y)=(k\cdot x,k\cdot y)}$

${\displaystyle 0\cdot (x,y)=(0,0).}$

Mnożenie przez ${\displaystyle -1}$ jest półobrotem wokół punktu ${\displaystyle O.}$ Dlatego mnożenie przez pierwiastek kwadratowy z ${\displaystyle -1}$ jest takim przekształceniem, którego kwadrat (czyli złożenie przekształcenia z samym sobą) jest półobrotem wokół punktu ${\displaystyle O,}$ czyli ćwierćobrót wokół punktu ${\displaystyle O}$ (czyli obrót o kąt prosty)^[8].

Mnożenie liczb zespolonych; współrzędne kartezjańskie

Mnożenie liczb zespolonych; współrzędne biegunowe

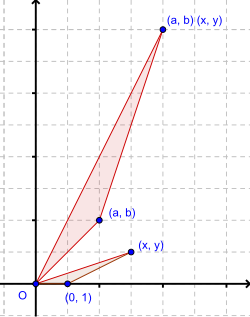
Wobec tego mnożenie przez dowolną liczbę zespoloną powinno być przekształceniem, dla którego punkt ${\displaystyle O}$ jest punktem stałym i które zawiera zarówno jednokładności o środku w ${\displaystyle O,}$ jak i obroty dokoła ${\displaystyle O}$ jako przypadki szczególne. Mnożenie dowolnego punktu ${\displaystyle (x,y)}$ przez ustalony punkt ${\displaystyle (a,b)}$ definiuje się jako podobieństwo spiralne o środku ${\displaystyle O,}$ które przeprowadza punkt ${\displaystyle (1,0)}$ w punkt ${\displaystyle (a,b)}$^[9]. Jeżeli punkty ${\displaystyle (a,b)}$ i ${\displaystyle (x,y)}$ mają współrzędne biegunowe odpowiednio ${\displaystyle (s,\eta )}$ i ${\displaystyle (r,\theta ),}$ czyli

${\displaystyle a=s\cos \eta ,\ b=s\sin \eta ,\ x=r\cos \theta ,\ y=r\sin \theta .}$

Wówczas podobieństwo spiralne, w którym mnoży się ${\displaystyle r}$ przez ${\displaystyle s}$ i dodaje ${\displaystyle \eta }$ do ${\displaystyle \theta ,}$ przekształca współrzędne

${\displaystyle r\cos \theta =x,\ r\sin \theta =y}$

na współrzędne

${\displaystyle {\begin{aligned}sr\cos(\theta +\eta )&=sr(\cos \theta \cos \eta -\sin \theta \sin \eta )\\&=(s\cos \eta )(r\cos \theta )-(s\sin \eta )(r\sin \theta )\\&=ax-by,\end{aligned}}}$

${\displaystyle {\begin{aligned}sr\sin(\theta +\eta )&=sr(\sin \theta \cos \eta -\cos \theta \sin \eta )\\&=(s\cos \eta )(r\sin \theta )-(s\sin \eta )(r\cos \theta )\\&=ay+bx.\end{aligned}}}$

Stąd wzór

${\displaystyle (a,b)(x,y)=(ax-by,\ ay+bx).}$