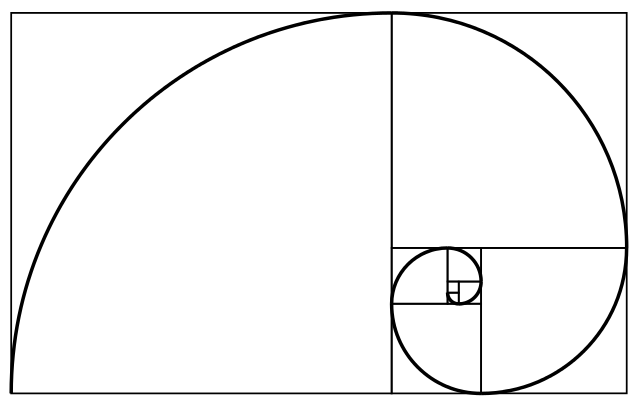
Złota spirala

Złota spirala – szczególny przypadek spirali logarytmicznej, w której współczynnik ${\displaystyle b}$ jest stałą zależną od ${\displaystyle \varphi }$ (gdzie ${\displaystyle \varphi }$ jest „złotą liczbą”). Cechą charakterystyczną złotej spirali jest to, że co 90° jej szerokość zwiększa się (lub zmniejsza) dokładnie ${\displaystyle \varphi }$ razy.

Przybliżona oraz dokładna złota spirala: zielona spirala jest zbudowana z ćwiartek okręgów, natomiast czerwona spirala jest złotą spiralą. Pokrywające się fragmenty zaznaczono na żółto. Stosunki długości boków kolejnych kwadratów są równe φ.

Spirala Fibonacciego, zbudowana z ćwiartek okręgów, których promienie są kolejnymi liczbami Fibonacciego. Jest przybliżeniem złotej spirali, ale nie jest złotą spiralą

Wzór

Ogólne wzory na spiralę logarytmiczną we współrzędnych biegunowych:

${\displaystyle r=ae^{b\theta }}$

oraz

${\displaystyle \theta ={\frac {1}{b}}\ln(r/a),}$

(gdzie ${\displaystyle e}$ – podstawa logarytmu naturalnego) mają również zastosowanie w przypadku złotej spirali. W tym przypadku ${\displaystyle \theta }$ jest kątem prostym, ${\displaystyle b}$ jest stałą rzeczywistą, zaś ${\displaystyle r/a=\varphi }$ (gdzie ${\displaystyle \varphi }$ jest „złotą liczbą”). Stąd mamy wzór:

${\displaystyle e^{b\theta }=\varphi .}$

Wartość ${\displaystyle b}$ wyraża się wzorem:

${\displaystyle b={\frac {\ln {\varphi }}{\theta }}.}$

Wartość ${\displaystyle b}$ może być dodatnia lub ujemna, w zależności od tego, w którą stronę skierowany jest kąt prosty ${\displaystyle \theta .}$ Wartość bezwzględna z ${\displaystyle b}$ wynosi:

${\displaystyle |b|={\frac {\ln \varphi }{90^{\circ }}}={\frac {0{,}0053468}{1^{\circ }}}}$ dla ${\displaystyle \theta }$ wyrażonego w stopniach;

${\displaystyle |b|={\frac {\ln \varphi }{\pi /2}}=0{,}306349}$ dla ${\displaystyle \theta }$ wyrażonego w radianach.

Przybliżenia złotej spirali

Znanych jest wiele spiral będących przybliżeniami złotej spirali i często mylonych z nią. Przykładem może być spirala Fibonacciego, która nie jest spiralą logarytmiczną.

Zobacz też

• ciąg Fibonacciego
• spirala
• spirala logarytmiczna
• złoty podział

Bibliografia

• Fractals in Music: introductory mathematics for musical analysis. High Art Press, 1999, s. 14–16. ISBN 0-9671727-6-4. (ang.).
• Divine Proportion: Φ Phi in Art, Nature, and Science. Sterling Publishing Co, 2005, s. 127–129. ISBN 1-4027-3522-7. (ang.).

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Golden Spiral, [w:] MathWorld, Wolfram Research (ang.). [dostęp 2025-07-19].
• Golden Spiral demonstracja autorstwa Yu-Sung Chang, The Wolfram Demonstrations Project