Grafo de Heawood

No campo da matemática da teoria dos grafos o grafo de Heawood é um grafo não-orientado com 14 vértices e 21 arestas.^[1] O grafo é cúbico, e todos os ciclos do grafo têm seis ou mais arestas. Todos os menores grafos cúbicos têm ciclos mais curtos, de modo que este grafo é o gaiola-6, o menor grafo cúbico de cintura 6.

Grafo de Heawood
Nomeado após	Percy John Heawood
Vértices	14
Arestas	21
Raio	3
Diâmetro	3
Cintura	6
Automorfismos	336 (PGL2(7))
Número cromático	2
Índice cromático	3
Propriedades	Cúbico gaiola distância-transitivo distância-regular Toroidal Hamiltoniano simétrico

É também o grafo de Levi do plano de Fano, o grafo que representa a incidência entre os pontos e linhas nesta geometria. É um grafo distância-regular; o seu grupo de simetrias é PGL₂(7).^[2]

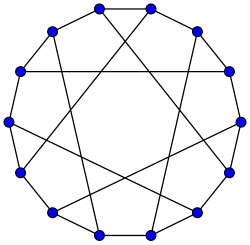
Há 24 correspondências perfeitas no grafo de Heawood; para cada correspondência, o conjunto de arestas fora das correspondências forma um ciclo Hamiltoniano. Por exemplo, a figura mostra os vértices do grafo colocados em um ciclo, com as diagonais internas do ciclo formando uma correspondência. Subdividindo as arestas do ciclo em duas correspondências, podemos particionar o grafo de Heawood em três correspondências perfeitas (isto é, usando 3 cores em suas arestas) em oito formas diferentes (Brouwer).

O grafo de Heawood foi batizado em honra de Percy John Heawood, que em 1890 provou que cada subdivisão do toro em polígonos pode ser colorida, no máximo, com sete cores.^[3][4] O grafo de Heawood forma uma subdivisão do toro com sete regiões adjacentes mutuamente, mostrando que esse limite é apertado.

O grafo de Heawood tem número de cruzamento 3, e é o menor grafo cúbico com este número de cruzamento. Incluindo o grafo de Heawood, existem 8 grafos distintos de ordem 14 com número de cruzamento 3.

O grafo de Heawood é um grafo distância-unidade.^[5]

Propriedades algébricas

O grupo de automorfismo do grafo de Heawood é isomórfico ao grupo linear projetivo PGL₂(7), um grupo de ordem 336.^[6] Ele atua transitivamente sobre os vértices, nas arestas e nos arcos do grafo. Portanto o grafo Heawood é um grafo simétrico. Ele tem automorfismos que levam qualquer vértice para qualquer outro vértice e qualquer aresta para qualquer outra aresta. De acordo com o censo Foster, o grafo de Heawood, referenciado como F014A, é o único grafo cúbico simétrico com 14 vértices.^[7][8]

O polinômio característico do grafo de Heawood é ${\displaystyle (x-3)(x+3)(x^{2}-2)^{6}}$. É o único grafo com este polinômio característico, tornando-se um grafo determinado pelo seu espectro.

Incorporado em um Toro

O grafo de Heawood é um grafo toroidal; ou seja, ele pode ser incorporado sem cruzamentos em um toro. Uma incorporação deste tipo coloca seus vértices e arestas em um espaço euclidiano tri-dimensional como o conjunto de vértices e arestas de um poliedro convexo com a topologia de um toro, o poliedro de Szilassi.

Galeria

• 
  O poliedro de Szilassi.
• 
  O grafo de Heawood tem número de cruzamento 3.
• 
  O índice cromático do grafo de Heawood é 3.
• 
  O número cromático do grafo de Heawood é 2.
• 
  A incorporação do grafo de Heawood em um toro (mostrado como um quadrado com condições de contorno periódicas) particionando-o em sete regiões mutuamente adjacentes

Referências

1. Weisstein, Eric W. «Heawood Graph». MathWorld (em inglês)
2. BROUWER, Andries E. «Heawood graph». Additions and Corrections to the book Distance-Regular Graphs(Brouwer, Cohen, Neumaier; Springer; 1989)
3. BROWN, Ezra (2002). «The many names of (7,3,1)» (PDF). Mathematics Magazine. 75 (2). pp. 83–94. JSTOR 3219140. doi:10.2307/3219140
4. Heawood, P. J. (1890). «Map colouring theorems». Quarterly J. Math. Oxford Ser. 24. pp. 322–339
5. GERBRACHT, Eberhard H.-A. (2009). «Eleven unit distance embeddings of the Heawood graph». Arxiv
6. BONDY, J. A.; MURTY, U. S. R. (1976). Graph Theory with Applications. New York: North Holland. p. 237. ISBN 0-444-19451-7. Consultado em 15 de outubro de 2010. Arquivado do original em 13 de abril de 2010 !CS1 manut: Nomes múltiplos: lista de autores (link)
7. Royle, G. "Cubic Symmetric Graphs (The Foster Census)." Arquivado em 20 de julho de 2008, no Wayback Machine.
8. Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002.