Hipocicloide

A Hipocicloide é uma curva cíclica definida por um ponto de uma circunferência que rola, sem deslizar, dentro de um círculo diretor^[1].

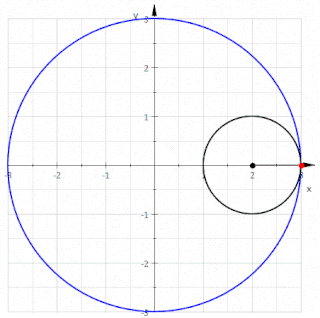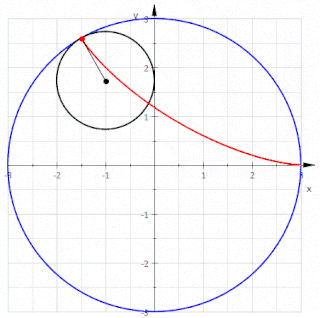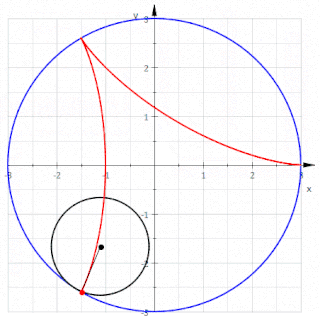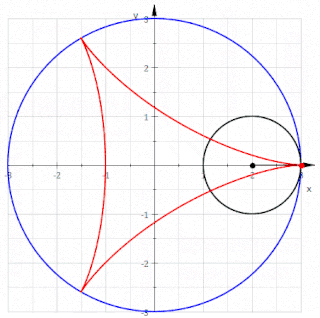
Definição Matemática

Uma Hipocicloide pode ser definida pelas seguintes equações paramétricas:

${\displaystyle f(\theta )=(R-r)\cos \theta +r\cos({\frac {R-r}{r}}\theta )\,\qquad (1)}$

${\displaystyle g(\theta )=(R-r)\operatorname {sen} \theta -r\operatorname {sen}({\frac {R-r}{r}}\theta )\,\qquad (2)}$

em que ${\displaystyle R,}$ é o raio do círculo base e ${\displaystyle r,}$ o raio do círculo rolante. Com ${\displaystyle k={R \over r}}$, este sistema também pode ser escrito:

${\displaystyle f(\theta )=r(k-1)\cos \theta +r\cos \left((k-1)\theta \right)\,}$

${\displaystyle g(\theta )=r(k-1)\operatorname {sen} \theta -r\operatorname {sen} \left((k-1)\theta \right).\,}$

Evoluta da Hipocicloide

Evoluta de uma hipocicloide com k = 5 e r = 5.

Na geometria diferencial de curvas, a evoluta da curva é o local de todos os seus centros de curvatura. A evoluta de uma hipocicloide é outra hipocicloide, como pode-se observar na figura ao lado. A evoluta de uma hipocicloide pode ser descrita pelas seguintes equações paramétricas:

${\displaystyle X_{e}(\theta )=f(\theta )-{\frac {(f'^{2}(\theta )+g'^{2}(\theta ))g'(\theta )}{f'(\theta )g''(\theta )-f''(\theta )g'(\theta )}}\,}$

${\displaystyle Y_{e}(\theta )=g(\theta )-{\frac {(f'^{2}(\theta )+g'^{2}(\theta ))f'(\theta )}{f'(\theta )g''(\theta )-f''(\theta )g'(\theta )}}\,}$

Involuta da Hipocicloide

Involuta de uma hipocicloide com k = 5 e r = 5

A involuta de uma hipocicloide é outra hipocicloide, como pode-se observar na figura ao lado. A involuta de uma hipocicloide pode ser descrita pelas seguintes equações paramétricas:

${\displaystyle X_{i}(\theta )=f(\theta )-{\frac {sf'(\theta )}{\sqrt {f'^{2}(\theta )+g'^{2}(\theta )}}}\,}$

${\displaystyle Y_{i}(\theta )=g(\theta )-{\frac {sg'(\theta )}{\sqrt {(f'^{2}(\theta )+g'^{2}(\theta )}}}\,}$

em que ${\displaystyle s}$ pode ser calculado da seguinte forma:

${\displaystyle s=\int _{0}^{\theta }{\sqrt {f'^{2}(\theta )+g'^{2}(\theta )}}d\theta \,}$

Encurtada

Hipocicloide Encurtada

Se o ponto da curva estiver dentro da circunferência, a curva descrita será uma hipocicloide encurtada, como na figura ao lado (curva vermelha)^[2].

Alongada

Hipocicloide Alongada

Se o ponto da curva estiver fora da circunferência, a curva descrita será uma hipocicloide alongada, como na figura ao lado (curva vermelha).^[2]

Exemplos

• Exemplos de hipocicloides
• 
  k=3 - uma deltóide
• 
  k=4 - uma astróide
• 
  k=5
• 
  k=6
• 
  k=2.1
• 
  k=3.8
• 
  k=5.5
• 
  k=7.2

Referências

1. Carvalho, Benjamim - Desenho Geométrico. Ed. Ao Livro Técnico, São Paulo: 1988, cap. 13, p. 288
2. Curvas cíclicas. Página acessada em 24-07-2011.