Двоичный логарифм

Двоичный логарифм — логарифм по основанию 2. Другими словами, двоичный логарифм числа ${\displaystyle b}$ есть решение уравнения ${\displaystyle 2^{x}=b.}$

График двоичного логарифма

Двоичный логарифм вещественного числа ${\displaystyle b}$ существует, если ${\displaystyle b>0.}$ Согласно стандарту ISO 31-11, он обозначается^[1] ${\displaystyle \operatorname {lb} b,}$ ${\displaystyle \operatorname {lb} (b)}$ или ${\displaystyle \log _{2}b}$. Примеры:

${\displaystyle \operatorname {lb} 1=0;\,\operatorname {lb} 2=1;\,\operatorname {lb} 16=4}$

${\displaystyle \operatorname {lb} 0{,}5=-1;\,\operatorname {lb} {\frac {1}{256}}=-8}$

История

Исторически двоичные логарифмы нашли своё первое применение в теории музыки, когда Леонард Эйлер установил: двоичный логарифм отношения частот двух музыкальных тонов равен количеству октав, которое отделяет один тон от другого. Эйлер также опубликовал таблицу двоичных логарифмов целых чисел от 1 до 8 с точностью до семи десятичных знаков^[2][3].

С созданием информатики выяснилось, что двоичные логарифмы необходимы для определения количества битов, требующихся для кодирования сообщения. Другие области, в которых часто используется двоичный логарифм, включают комбинаторику, биоинформатику, криптографию, проведение спортивных турниров и фотографию. Стандартная функция для вычисления двоичного логарифма предусмотрена во многих распространённых системах программирования.

Алгебраические свойства

В нижеследующей таблице предполагается, что все значения положительны^[4]:

	Формула	Пример
Произведение	${\displaystyle \operatorname {lb} (xy)=\operatorname {lb} (x)+\operatorname {lb} (y)}$	${\displaystyle \operatorname {lb} (256)=\operatorname {lb} (16\cdot 16)=\operatorname {lb} (16)+\operatorname {lb} (16)=4+4=8}$
Частное от деления	${\displaystyle \operatorname {lb} \!\left({\frac {x}{y}}\right)=\operatorname {lb} (x)-\operatorname {lb} (y)}$	${\displaystyle \operatorname {lb} \left({\frac {1}{32}}\right)=\operatorname {lb} (1)-\operatorname {lb} (32)=0-5=-5}$
Степень	${\displaystyle \operatorname {lb} (x^{p})=p\operatorname {lb} (x)}$	${\displaystyle \operatorname {lb} (1024)=\operatorname {lb} (2^{10})=10\operatorname {lb} (2)=10}$
Корень	${\displaystyle \operatorname {lb} {\sqrt[{p}]{x}}={\frac {\operatorname {lb} (x)}{p}}}$	${\displaystyle \operatorname {lb} {\sqrt {8}}={\frac {1}{2}}\operatorname {lb} 8={\frac {3}{2}}=1{,}5}$

Существует очевидное обобщение приведенных формул на случай, когда допускаются отрицательные переменные, например:

${\displaystyle \operatorname {lb} |xy|=\operatorname {lb} (|x|)+\operatorname {lb} (|y|),}$

${\displaystyle \operatorname {lb} \!\left|{\frac {x}{y}}\right|=\operatorname {lb} (|x|)-\operatorname {lb} (|y|),}$

Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:

${\displaystyle \operatorname {lb} (x_{1}x_{2}\dots x_{n})=\operatorname {lb} (x_{1})+\operatorname {lb} (x_{2})+\dots +\operatorname {lb} (x_{n})}$

Связь двоичного, натурального и десятичного логарифмов:

${\displaystyle \operatorname {lb} x\approx 1{,}442695\ln x}$

${\displaystyle \operatorname {lb} x\approx 3{,}321928\lg x}$

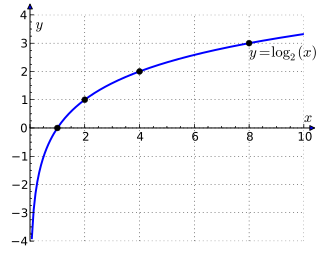
Функция двоичного логарифма

Если рассматривать логарифмируемое число как переменную, мы получим функцию двоичного логарифма: ${\displaystyle y=\operatorname {lb} x}$. Она определена при всех ${\displaystyle x>0,}$ область значений: ${\displaystyle E(y)=(-\infty$ ;+\infty )} . График этой функции часто называется логарифмикой, она обратна для функции ${\displaystyle y=2^{x}}$. Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой^[5]:

${\displaystyle {\frac {d}{dx}}\operatorname {lb} x={\frac {\operatorname {lb} e}{x}}}$

Ось ординат ${\displaystyle (x=0)}$ является вертикальной асимптотой, поскольку:

${\displaystyle \lim _{x\to 0+0}\operatorname {lb} x=-\infty }$

Применение

Теория информации

Двоичный логарифм натурального числа ${\displaystyle N}$ позволяет определить число цифр ${\displaystyle b(N)}$ во внутреннем компьютерном (битовом) представлении этого числа:

${\displaystyle b(N)=\lfloor \operatorname {lb} N\rfloor +1}$ (скобки обозначают целую часть числа)

Информационная энтропия — мера количества информации, также основана на двоичном логарифме

Сложность рекурсивных алгоритмов

Оценка асимптотической сложности рекурсивных алгоритмов, основанных на принципе «разделяй и властвуй»^[6] — таких, как быстрая сортировка, быстрое преобразование Фурье, двоичный поиск и т. п.

Комбинаторика

Если двоичное дерево содержит ${\displaystyle n}$ узлов, то его высота не меньше, чем ${\displaystyle \log _{2}n}$ (равенство достигается, если ${\displaystyle n}$ является степенью 2)^[7]. Соответственно, число Стралера — Философова для речной системы с ${\displaystyle n}$ притоками не превышает^[8] ${\displaystyle \log _{2}n+1}$.

Изометрическая размерность частичного куба с ${\displaystyle n}$ вершинами не меньше, чем ${\displaystyle \log _{2}n.}$ Число рёбер куба не более, чем ${\displaystyle {\frac {1}{2}}n\log _{2}n,}$ равенство имеет место, когда частичный куб является графом гиперкуба^[9].

Согласно теореме Рамсея, неориентированный граф с ${\displaystyle n}$ вершинами содержит либо клику, либо независимое множество, размер которого логарифмически зависит от ${\displaystyle n.}$ Точный размер этого множества неизвестен, но наилучшие в настоящий момент оценки содержат двоичные логарифмы.

Другие применения

Число кругов игры по олимпийской системе равно двоичному логарифму от числа участников соревнований^[10].

В теории музыки, чтобы решить вопрос о том, на сколько частей делить октаву, требуется отыскать рациональное приближение для ${\displaystyle \log _{2}{\frac {3}{2}}\approx 0{,}585.}$ Если разложить это число в непрерывную дробь, то третья подходящая дробь (7/12) позволяет обосновать классическое деление октавы на 12 полутонов^[11].