Конциклические точки

Конциклические точки (или гомоциклические точки) — точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек^[1].

Пересекающиеся в центре срединные перпендикуляры, проведённые к хордам круга, соединяющим всевозможные пары трёх конциклических точек

Четыре конциклические точки, являющиеся сторонами вписанного в окружность четырехугольника. На рис. показаны два равных угла

Серединные перпендикуляры

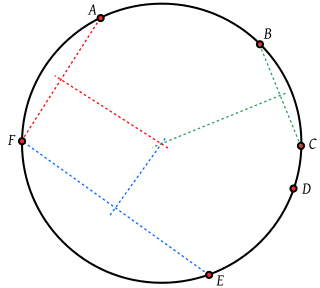
В общем случае центр O окружности, на которой лежат точки P и Q, должен быть таким, чтобы расстояния OP и OQ были равны . Поэтому точка O должна лежать на срединном перпендикуляре (или на медиатрисе) отрезка PQ^[2]. Необходимым и достаточным условием того, чтобы n различных точек лежали на одной окружности является то, что n(n − 1)/2 медиатрис отрезков, имеющих своими концами любые пары из n точек, все одновременно пересекались в одной точке, а именно: в центре O.

Вписанные многоугольники

Треугольники

Вершины каждого треугольника лежат на окружности^[3]. Окружность, проходящая через 3 вершины треугольника, называется описанной окружностью треугольника. Несколько других наборов точек, которые определяются из треугольника, также лежат на одной окружности, то есть являются конциклическими точками; см. Окружность Эйлера^[4] и Окружность Лестера^[5].

Радиус окружности, на которой находятся множество точек, по определению, есть радиус описанной окружности любого треугольника с вершинами в любых трёх из этих точек. Если попарные расстояния между любыми тремя из этих точек a, b и c, то радиус окружности равен

${\displaystyle R={\sqrt {\frac {a^{2}b^{2}c^{2}}{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}.}$

Уравнение описанной окружности для треугольника, и выражение для радиуса и координат центра окружности через декартовы координаты вершин приведены здесь.

Четырехугольники

Четырехугольник ABCD с вершинами, лежащими на одной окружности, называется вписанным; это бывает тогда и только тогда, когда ${\displaystyle \angle CAD=\angle CBD}$ (по теореме о вписанном угле окружности), что выполняется если и только если противоположные углы четырёхугольника дополняют друг друга до 180 градусов^[6]. Вписанный четырёхугольник с последовательными сторонами a, b, c, d и полупериметром s = (a+b+c+d)/2 имеет радиус описанной окружности, равный^[7][8]

${\displaystyle R={\frac {1}{4}}{\sqrt {\frac {(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}}.}$

Это выражение было получено индийским математиком Ватассери Парамешвара^[англ.] в XV веке.

По теореме Птолемея, четырёхугольник, заданный попарными расстояниями между его четырьмя вершинами A, B, C и D соответственно, будет вписанным тогда и только тогда, когда произведение его диагоналей равно сумме произведений противоположных сторон:

${\displaystyle AC\cdot BD=AB\cdot CD+BC\cdot AD.}$

Если две прямые, одна из которых содержит отрезок AC, а другая содержит отрезок BD, пересекаются в одной точке «Х», то эти четыре точки A, B, C, D являются конциклическими точками тогда и только тогда, когда^[9]

${\displaystyle \displaystyle AX\cdot XC=BX\cdot XD.}$

Точка пересечения X может быть как внутри, так и вне описанного круга. Эта теорема известна как теорема о степени точки.

n-угольники

В общем случае n-угольник, все вершины которого лежат на одной окружности, называется вписанным многоугольником. Многоугольник является вписанным многоугольником, если и только если все серединные перпендикуляры его сторон пересекаются в одной точке^[10].