Неравенство Птолемея

Неравенство Птолемея — неравенство на 6 расстояний между четвёркой точек ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ и ${\displaystyle D}$ на плоскости:

${\displaystyle AC\cdot BD\leqslant AB\cdot CD+BC\cdot AD}$,

Если 4 точки не лежат на одной окружности, то все три неравенства Птолемея строгие.

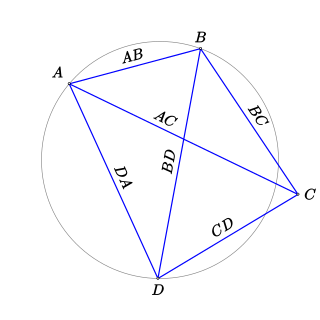
причём равенство достигается тогда и только тогда, когда ${\displaystyle ABCD}$ — выпуклый вписанный четырёхугольник, или точки ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ и ${\displaystyle D}$ лежат на одной прямой (тождество Птолемея). Доказано Клавдием Птолемеем в «Альмагесте».

Простейшее доказательство получается с использованием свойств комплексных чисел с использованием неравенства треугольника. Один из вариантов доказательства основан на применении инверсии относительно окружности с центром в точке ${\displaystyle A}$; этим неравенство Птолемея сводится к неравенству треугольника для образов точек ${\displaystyle B}$, ${\displaystyle C}$, ${\displaystyle D}$^[1]. Существует способ доказательства через прямую Симсона. Близкий к птолемеевскому доказательству способ — ввести точку ${\displaystyle E}$ такую, что ${\displaystyle \angle ABE=\angle DBC}$, после чего установить подобие треугольников. Также утверждение является следствием из соотношения Бретшнайдера.

Следствия, вариации и обобщения

Среди многочисленных непосредственных следствий — теорема Помпею^[2], теорема ван Схотена и формула Карно. Если ${\displaystyle AC}$ — диаметр окружности, то теорема превращается в правило синуса суммы — именно это следствие использовал Птолемей для составления таблицы синусов.

Тождество Птолемея является непосредственным следствием соотношения Бретшнайдера.

Неравенства Птолемея можно распространить и на шесть произвольны точек плоскости ${\displaystyle A_{1},A_{2},\dots A_{6}}$ (теорема Птолемея для шестиугольника, теорема Фурмана)^[3]):

${\displaystyle {\begin{aligned}A_{1}A_{4}\cdot A_{2}A_{5}\cdot A_{3}A_{6}\leqslant \,&\\&A_{1}A_{2}\cdot A_{3}A_{6}\cdot A_{4}A_{5}+A_{1}A_{2}\cdot A_{3}A_{4}\cdot A_{5}A_{6}+\\+&A_{2}A_{3}\cdot A_{1}A_{4}\cdot A_{5}A_{6}+A_{2}A_{3}\cdot A_{4}A_{5}\cdot A_{1}A_{6}+\\+&A_{3}A_{4}\cdot A_{2}A_{5}\cdot A_{1}A_{6}\end{aligned}}}$,

причём равенство достигается тогда и только тогда, когда ${\displaystyle A_{1}\dots A_{6}}$ — вписанный шестиугольник.

Теорема Кейси (также известная как обобщённая теорема Птолемея) формулируется для четырёх окружностей, касающихся данной окружности в вершинах выпуклого четырёхугольника, при радиусе окружностей, равном нулю, обращается в тождество Птолемея.

Циклический граф, в котором все расстояния удовлетворяют неравенству Птолемея, называют графом Птолемея

Граф Птолемея^[4] — граф, в котором расстояния по кратчайшему пути удовлетворяют неравенству Птолемея.