Кубика

Куби́ка или ку́бика — плоская алгебраическая кривая 3-го порядка, то есть множество точек плоскости (проективной или аффинной), заданных кубическим уравнением

${\displaystyle F\left(x,y,z\right)=0,}$

Набор кубик

которое применяется к однородным координатам на проективной плоскости. Чтобы перейти к аффинной версии, достаточно положить z = 1.

Иногда кубикой также называют гиперповерхность 3-го порядка в пространстве произвольной размерности^[1].

Ударение

В Математическом энциклопедическом словаре приведено ударение «куби́ка»^[1]. В другом словаре — «ку́бика»^[2]. В разговорном языке употребляется произношение с ударением на первый слог: «ку́бика»^{[3][4][5][6][7]}.

Классификация

Первая классификация кубик была дана Ньютоном в 1704 году^[8].

Ньютон доказал, что для любой кубики можно подобрать систему координат, в которой она будет иметь один из следующих видов:

• ${\displaystyle xy^{2}+ey\,=\,ax^{3}+bx^{2}+cx+d}$;
• ${\displaystyle xy\,=\,ax^{3}+bx^{2}+cx+d}$;
• ${\displaystyle y^{2}\,=\,ax^{3}+bx^{2}+cx+d}$;
• ${\displaystyle y\,=\,ax^{3}+bx^{2}+cx+d}$.

Далее Ньютон поделил все кривые на классы, роды и типы, пропустив при этом, однако, 6 типов. Полную классификацию дал Плюккер^[9].

По состоянию на 2008 год, аналогичной классификации для кривых n-го порядка не найдено, эта задача составляет 16-ю проблему Гильберта.

Свойства

Кубика y² = x² · (x + 1). Параметризация: t → (t² − 1, t · (t² − 1))

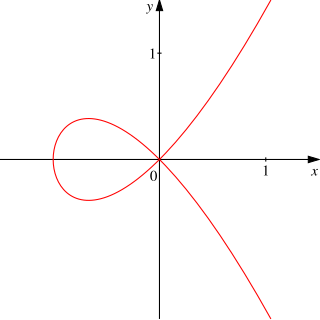
• Теорема о девяти точках на кубике (теорема Шаля): даны две кубики A и B, имеющие 9 общих точек. Если третья кубика С проходит через 8 из них, то она проходит и через девятую.
• На кубике взяли точку A и провели из неё 2 касательных к кубике — одна касается кубики в точке A, другая — в точке B. Пусть площади сегментов, отсекаемых этими касательными от графика кубики, равны X и Y. Тогда X = 16Y^[10].
• Известно, что некоторые кубики являются трисектрисами, то есть если на плоскости нарисован график такой кубики и дан угол, то его можно разделить циркулем и линейкой на 3 равные части. Открытая проблема: любая ли кубика является трисектрисой?
• Максимально возможное число компонент связности у графика кубики в ℝ² есть 4. Например, у кубики f (x, y) = 3x³ − 5y²x − 4x² − 10yx + 10y² − 6x + 20y + 12 график состоит из трёх удаляющихся на бесконечность кривых и одной изолированной точки.
• Если прямая проходит через две точки перегиба кубики, то она проходит и через третью.
• На кубиках можно ввести сложение точек и умножение их на число, получив тем самым алгебраическую структуру, называемую эллиптической кривой^[11][12].
• Прямая пересекает кубику в точках A, B, C. Касательные, восстановленные к кубике в точках A, B, C, пересекают кубику второй раз в точках P, Q, R. Тогда точки P, Q, R также лежат на одной прямой^[13][14].

Применения

• Кубические кривые применяются в языке PostScript, включая шрифты формата Type 1 (в TrueType используются только квадратичные кривые).
• Изучение кубик долгое время считалось примером чистой математики (не имеющей никакого прикладного применения и перспективы такового). Однако в последние 20 лет XX века были придуманы криптографические алгоритмы, использующие глубокие свойства кубик, которые сегодня используются (в частности) при банковском шифровании, что дало толчок изучению свойств кубик, см. Эллиптическая криптография.
• Большое число замечательных точек треугольника складываются в несколько кубик^[15].
• Фрэнк Морли доказал известную теорему, названную в его честь, изучая свойства кубик^[16].

См. также

• Теорема о девяти точках на кубике
• Кубики, связанные с треугольником
• Эллиптическая кривая
• Классификации кубик Ньютона
• Аффинная классификация кубик
• Изометрическая эквивалентность
• Аффинная эквивалентность