Пара Туси

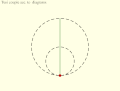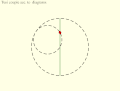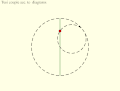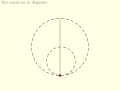
Пара Туси или Механизм Туси^[1][2][3] — частный случай гипоциклоиды в евклидовой плоскости, в которой малый круг вращается без проскальзывания внутри круга вдвое большего диаметра. При движении каждая точка на окружности меньшего круга описывает диаметр большого круга.

Пара Туси

История

Схема пары Туси, сделанная ат-Туси в XIII-м веке^[4]

Пара была предложена в 1247 году персидским астрономом и математиком Насир ад-Дином ат-Туси как объяснение широтного движения низших планет^[5], и позднее использовалась в качестве замены эквант^[6][7].

Это одно из нескольких позднеисламских астрономических устройств, которые схожи с моделями в главной работе Коперника О вращениях небесных сфер, включая его модель Меркурия и теорию трепидации – он использовал эту конструкцию для разложения (кажущихся) линейных колебательных движений Земли и других планет на две круговые траектории^[8]. Историки подозревают, что Коперник прямо или косвенно имел доступ к арабскому астрономическому первоисточнику^[9]. Например, учёный и путешественник XVI века Гийом Постель, который привёз из Османской империи работы ат-Туси и написал к ним комментарии, был предложен в качестве одного из возможных посредников^[10][11]. Примечательно, что в работах Коперника^[12] точки были названы фонетически аналогично названиям в работах ат-Туси^[13][14].

Технические применения

С помощью пары Туси можно преобразовать вращательное движение в периодическое прямолинейное

Печатные машины

Этот принцип лежал в основе устройства скоропечатных машин фирмы «Кёниг и Бауэр».

Двигатели

Джеймс Уайт в 1801 году получил медаль от Наполеона Бонапарта за паровую машину, использующую гипоциклоидное прямолинейное движение. По проекту Уайта было построено несколько машин, но экономический успех не был достигнут^[15][16].

Мэтью Мюррей разработал гипоциклоидную паровую машину в 1802 году^[17][18].

Общие сведения

В технических применениях этот механизм также известен как гипоциклоидная прямолинейная передача^[19].

В коллекции механизмов Франца Рело находятся две модели гипоциклоидных прямолинейных передач^[20][21].

Галерея

• 
• 
• 
• 
•