Гипоциклоида

Гипоцикло́ида (греч. ὑπό(под, внизу) + греч. κύκλος(круг, окружность)) — плоская, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения^[1].

История

Схема гипоциклоиды с k=2 (пара Туси), сделанная ат-Туси в XIII-м веке^[2]

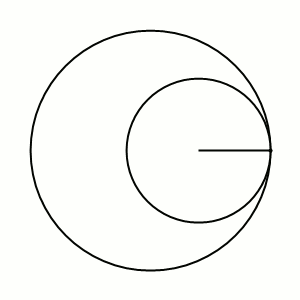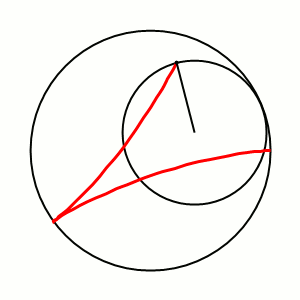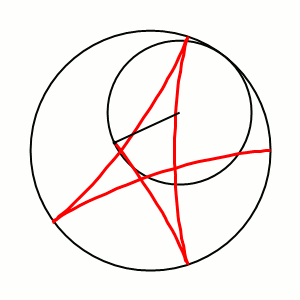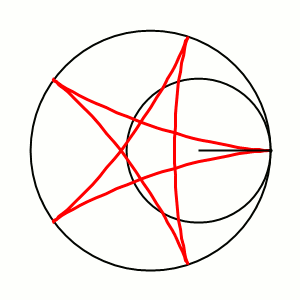
Впервые частный случай гипоциклодиды, который сейчас известен как пара Туси, был описан астрономом и математиком Насир ад-Дином ат-Туси в его труде Тахрир аль-Маджисти в 1247 году^[3][4]. Позднее немецкий художник и теоретик эпохи Ренессанса Альбрехт Дюрер описал эпитрохоиды в 1525 году, а Рёмер и Бернулли сосредоточились на изучении некоторых специфических гипоциклоид, таких как астроиды, в 1674 и 1691 годах соответственно.

Уравнения

Внутри воздушного шарика катится маленькая батарейка с прикреплённым светодиодом, видна гипоциклоида с k=9

Параметрические уравнения:

${\displaystyle {\begin{cases}x=r(k-1)\left(\cos t+{\frac {\cos((k-1)t)}{k-1}}\right)\\y=r(k-1)\left(\sin t-{\frac {\sin((k-1)t)}{k-1}}\right)\end{cases}}}$

где ${\displaystyle \textstyle k={\frac {R}{r}}}$, где ${\displaystyle R}$ — радиус неподвижной окружности, ${\displaystyle r}$ — радиус катящейся окружности.

Вывод уравнений Пусть в начальный момент окружности касаются в точке ${\displaystyle A}$, лежащей на оси ${\displaystyle OX}$, где точка ${\displaystyle O}$ — центр большой окружности. Координаты точки ${\displaystyle A}$ при этом - ${\displaystyle (kr,0)}$, где ${\displaystyle k={\frac {R}{r}}}$. Рассмотрим, как меняются координаты точки ${\displaystyle A}$, привязанной к катящейся окружности (${\displaystyle A}$ переходит в ${\displaystyle A'}$). Пусть маленькая окружность прокатилась так, что её центр перешел из точки ${\displaystyle C'}$ в точку ${\displaystyle C'}$ и повернулся относительно точки ${\displaystyle O}$ на угол ${\displaystyle t}$. Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между ${\displaystyle CA}$ и ${\displaystyle C'A'}$) равен ${\displaystyle t-kt=-(k-1)t}$. Во-вторых, координаты точки ${\displaystyle C'}$ будут такими: ${\displaystyle (cos(t)(k-1)r,sin(t)(k-1)r)}$. Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты точки ${\displaystyle A'}$: ${\displaystyle {\begin{cases}x=cos(t)(k-1)r+cos((k-1)t)r\\y=sin(t)(k-1)r-sin((k-1)t)r\end{cases}}}$

Модуль величины ${\displaystyle k}$ определяет форму гипоциклоиды. При ${\displaystyle k=2}$ гипоциклоида описывается парой Туси — это диаметр неподвижной окружности, при ${\displaystyle k=4}$ является астроидой. Если модуль ${\displaystyle k}$ — несократимая дробь вида ${\displaystyle {\frac {m}{n}}}$ (${\displaystyle m,n\in \mathbb {N} }$), то ${\displaystyle m}$ — это количество каспов данной гипоциклоиды, а ${\displaystyle (m-n)}$ — количество полных вращений катящейся окружности. Если модуль ${\displaystyle k}$ иррациональное число, то кривая является незамкнутой и имеет бесконечное множество несовпадающих каспов.

Примеры гипоциклоид

${\displaystyle k=3}$ — Дельтоида ${\displaystyle k=1.5={\frac {3}{2}}}$ ${\displaystyle k=4}$ — Астроида ${\displaystyle k={\frac {4}{3}}}$ ${\displaystyle k=5}$ ${\displaystyle k=6}$ ${\displaystyle k=5.5={\frac {11}{2}}}$ ${\displaystyle k={\frac {5}{3}}}$ ${\displaystyle k=3.6={\frac {18}{5}}}$

См. также

• Циклоида
• Эпициклоида
• Гипотрохоида