Лучшие вопросы
Таймлайн
Чат
Перспективы
Риманова поверхность
математический объект Из Википедии, свободной энциклопедии
Remove ads
Ри́манова пове́рхность — математический объект, традиционное в комплексном анализе название одномерного комплексного дифференцируемого многообразия.

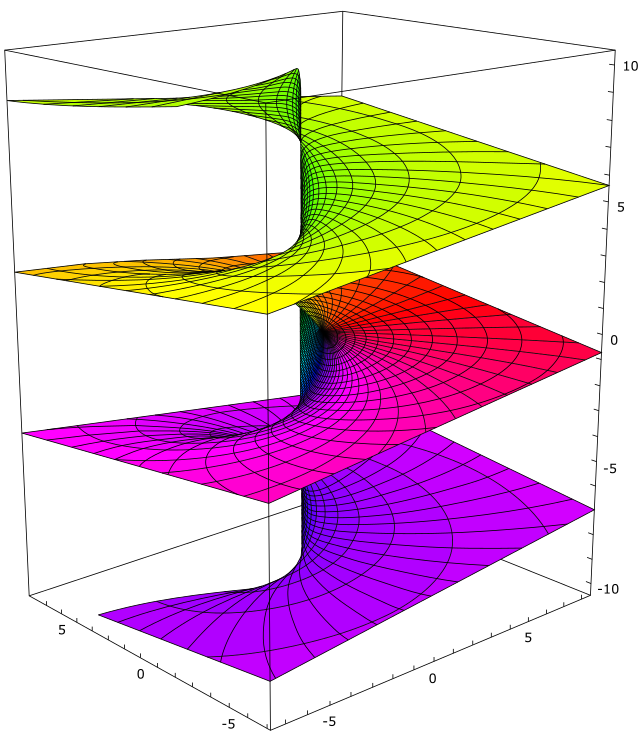

Примерами римановых поверхностей являются комплексная плоскость и сфера Римана. Поверхность Римана позволяет геометрически представить многозначные функции комплексной переменной таким образом, что каждой её точке соответствует одно значение многозначной функции, причём при непрерывном перемещении по поверхности непрерывно изменяется и функция[1]. Каноническим видом поверхности Римана является представление в виде плоской лепёшки с некоторым количеством дыр[2].
Топологической характеристикой римановой поверхности является род; поверхность рода — это сфера, поверхность рода — тор[3].
Remove ads
История
Поверхности такого рода систематически изучать начал Бернхард Риман (1826—1866).
По мнению Феликса Клейна, идея римановой поверхности принадлежит еще Галуа: в предсмертном письме он упоминает среди своих достижений какие-то исследования по «двусмысленности функций» (фр. ambiguïté des functions)[4].
См. также
Примечания
Литература
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads





