Сингулярное разложение

Сингуля́рное разложе́ние — определённого типа разложение прямоугольной матрицы, имеющее широкое применение, в силу своей наглядной геометрической интерпретации, при решении многих прикладных задач. Переформулировка сингулярного разложения, так называемое разложение Шмидта, имеет приложения в квантовой теории информации, например, в запутанности.

Геометрический смысл сингулярного разложения в двумерном случае.

Сингулярное разложение матрицы ${\displaystyle M}$ позволяет вычислять сингулярные числа данной матрицы, а также левые и правые сингулярные векторы матрицы ${\displaystyle M}$:

• левые сингулярные векторы матрицы ${\displaystyle M}$ — это собственные векторы матрицы ${\displaystyle MM^{*}}$;
• правые сингулярные векторы матрицы ${\displaystyle M}$ — это собственные векторы матрицы ${\displaystyle M^{*}M}$.

Где ${\displaystyle M^{*}}$— эрмитово-сопряжённая матрица к матрице ${\displaystyle M}$, для вещественной матрицы ${\displaystyle M^{*}=M^{T}}$.

Сингулярные числа матрицы не следует путать с собственными числами той же матрицы.

Сингулярное разложение является удобным при вычислении ранга матрицы, ядра матрицы и псевдообратной матрицы.

Сингулярное разложение также используется для приближения матриц матрицами заданного ранга.

Определение

Пусть матрица ${\displaystyle M}$ порядка ${\displaystyle m\times n}$ состоит из элементов из поля ${\displaystyle K}$, где ${\displaystyle K}$ — либо поле вещественных чисел, либо поле комплексных чисел.

Сингулярные числа и сингулярные векторы

Неотрицательное вещественное число ${\displaystyle \sigma }$ называется сингулярным числом матрицы ${\displaystyle M}$, когда существуют два вектора единичной длины ${\displaystyle u\in K^{m}}$ и ${\displaystyle v\in K^{n}}$ такие, что:

${\displaystyle Mv=\sigma u,}$ и ${\displaystyle M^{*}u=\sigma v.}$

Такие векторы ${\displaystyle u}$ и ${\displaystyle v}$ называются, соответственно, левым сингулярным вектором и правым сингулярным вектором, соответствующим сингулярному числу ${\displaystyle \sigma }$.

Разложение матрицы

Сингулярным разложением матрицы ${\displaystyle M}$ размера ${\displaystyle m\times n}$ является разложение следующего вида

${\displaystyle M=U\Sigma V^{*},}$

где ${\displaystyle \Sigma }$ — матрица размера ${\displaystyle m\times n}$ с неотрицательными элементами, у которой элементы, лежащие на главной диагонали — это сингулярные числа, а все элементы, не лежащие на главной диагонали, нулевые, матрицы ${\displaystyle U}$ (размера ${\displaystyle m}$) и ${\displaystyle V}$ (размера ${\displaystyle n}$) — это две унитарные матрицы, состоящие из левых и правых сингулярных векторов соответственно (${\displaystyle V^{*}}$ — эрмитово-сопряжённая матрица к ${\displaystyle V}$).

Пример

Пусть дана матрица:

${\displaystyle M={\begin{bmatrix}1&0&0&0&2\\0&0&3&0&0\\0&0&0&0&0\\0&4&0&0&0\end{bmatrix}}}$

Одним из сингулярных разложений этой матрицы является разложение ${\displaystyle M=U\Sigma V^{*}}$, где матрицы ${\displaystyle U}$, ${\displaystyle \Sigma }$ и ${\displaystyle V^{*}}$ следующие:

${\displaystyle U={\begin{bmatrix}0&0&1&0\\0&1&0&0\\0&0&0&-1\\1&0&0&0\end{bmatrix}},\quad \Sigma ={\begin{bmatrix}4&0&0&0&0\\0&3&0&0&0\\0&0&{\sqrt {5}}&0&0\\0&0&0&0&0\end{bmatrix}},\quad V^{*}={\begin{bmatrix}0&1&0&0&0\\0&0&1&0&0\\{\sqrt {0.2}}&0&0&0&{\sqrt {0.8}}\\0&0&0&1&0\\-{\sqrt {0.8}}&0&0&0&{\sqrt {0.2}}\end{bmatrix}},}$

так как матрицы ${\displaystyle U}$ и ${\displaystyle V}$ унитарны (${\displaystyle UU^{*}=I}$ и ${\displaystyle VV^{*}=I}$, где ${\displaystyle I}$ — единичная матрица), а ${\displaystyle \Sigma }$ — прямоугольная диагональная матрица, то есть ${\displaystyle \Sigma _{ij}=0}$, если ${\displaystyle i\neq j}$.

Геометрический смысл

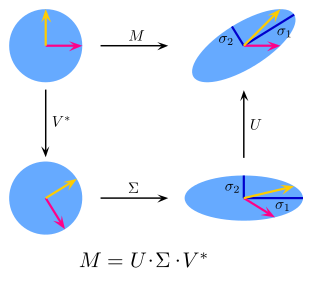
Пусть матрице ${\displaystyle A}$ поставлен в соответствие линейный оператор. Сингулярное разложение можно переформулировать в геометрических терминах. Линейный оператор, отображающий элементы пространства ${\displaystyle \mathbb {R} ^{n}}$ в себя, представим в виде последовательно выполняемых линейных операторов вращения и растяжения. Поэтому компоненты сингулярного разложения наглядно показывают геометрические изменения при отображении линейным оператором ${\displaystyle A}$ множества векторов из векторного пространства в себя или в векторное пространство другой размерности^[1].

Для более визуального представления рассмотрим сферу ${\displaystyle S}$ единичного радиуса в пространстве ${\displaystyle \mathbb {R} ^{n}}$. Линейное отображение ${\displaystyle T}$ отображает эту сферу в эллипсоид пространства ${\displaystyle \mathbb {R} ^{m}}$. Тогда ненулевые сингулярные значения диагонали матрицы ${\displaystyle \Sigma }$ являются длинами полуосей этого эллипсоида. В случае когда ${\displaystyle n=m}$ и все сингулярные величины различны и отличны от нуля, сингулярное разложение линейного отображения ${\displaystyle T}$ может быть легко проанализировано как последствие трех действий: рассмотрим эллипсоид ${\displaystyle T(S)}$ и его оси; затем рассмотрим направления в ${\displaystyle \mathbb {R} ^{n}}$, которые отображение ${\displaystyle T}$ переводит в эти оси. Эти направления ортогональны. Вначале применим изометрию ${\displaystyle \mathbf {v} ^{*}}$, отобразив эти направления на координатные оси ${\displaystyle \mathbb {R} ^{n}}$. Вторым шагом применим эндоморфизм ${\displaystyle \mathbf {d} }$, диагонализированный вдоль координатных осей и расширяющий/сжимающий эти направления, используя длины полуосей ${\displaystyle T(S)}$ как коэффициенты растяжения. Тогда произведение ${\displaystyle \mathbf {d} \otimes \mathbf {v} ^{*}}$ отображает единичную сферу на изометричный эллипсоид ${\displaystyle T(S)}$. Для определения последнего шага ${\displaystyle u}$ просто применим изометрию к этому эллипсоиду так, чтобы перевести его в ${\displaystyle T(S)}$. Как можно легко проверить, произведение ${\displaystyle \mathbf {u} \otimes \mathbf {d} \otimes \mathbf {v} ^{*}}$ совпадает с ${\displaystyle T}$.

Приложения

Псевдообратная матрица

Сингулярное разложение может быть использовано для нахождения псевдообратных матриц, которые применяются, в частности, в методе наименьших квадратов.

Если ${\displaystyle M=U\Sigma V^{*}}$, то псевдообратная к ней матрица находится по формуле:

${\displaystyle M^{+}=V\Sigma ^{-1}U^{*},}$

где ${\displaystyle \Sigma ^{-1}}$ — псевдообратная к матрице ${\displaystyle \Sigma }$, получающаяся из неё заменой каждого диагонального элемента ${\displaystyle \sigma }$ на обратный к нему: ${\displaystyle \sigma ^{-1}}$ и транспонированием.

Приближение матрицей меньшего ранга

В некоторых практических задачах требуется приближать заданную матрицу ${\displaystyle M}$ некоторой другой матрицей ${\displaystyle M_{k}}$ с заранее заданным рангом ${\displaystyle k}$. Известна следующая теорема, которую иногда называют теоремой Эккарта — Янга.^[2]

Если потребовать, чтобы такое приближение было наилучшим в том смысле, что евклидова норма разности матриц ${\displaystyle M}$ и ${\displaystyle M_{k}}$ минимальна, при ограничении ${\displaystyle {\mbox{rank}}(M_{k})=k}$, то оказывается, что наилучшая такая матрица ${\displaystyle M_{k}}$ получается из сингулярного разложения матрицы ${\displaystyle M}$ по формуле:

${\displaystyle M_{k}=U\Sigma _{k}V^{*},}$

где ${\displaystyle \Sigma _{k}}$ — матрица ${\displaystyle \Sigma }$, в которой заменили нулями все диагональные элементы, кроме ${\displaystyle k}$ наибольших элементов.

Если элементы матрицы ${\displaystyle \Sigma }$ упорядочены по невозрастанию, то выражение для матрицы ${\displaystyle M_{k}}$ можно переписать в такой форме:

${\displaystyle M_{k}=U_{k}\Sigma _{k}V_{k}^{*},}$

где матрицы ${\displaystyle U_{k}}$, ${\displaystyle \Sigma _{k}}$ и ${\displaystyle V_{k}}$ получаются из соответствующих матриц в сингулярном разложении матрицы ${\displaystyle M}$ обрезанием до ровно ${\displaystyle k}$ первых столбцов.

Таким образом видно, что приближая матрицу ${\displaystyle M}$ матрицей меньшего ранга, мы выполняем своего рода сжатие информации, содержащейся в ${\displaystyle M}$: матрица ${\displaystyle M}$ размера ${\displaystyle m\times n}$ заменяется меньшими матрицами размеров ${\displaystyle m\times k}$ и ${\displaystyle k\times n}$ и диагональной матрицей с ${\displaystyle k}$ элементами. При этом сжатие происходит с потерями — в приближении сохраняется лишь наиболее существенная часть матрицы ${\displaystyle M}$.

Во многом благодаря этому свойству сингулярное разложение и находит широкое практическое применение: в сжатии данных, обработке сигналов, численных итерационных методах для работы с матрицами, методе главных компонент, латентно-семантическом анализе и прочих областях.

Сокращенное представление

Для матрицы ${\displaystyle M}$ порядка ${\displaystyle m\times n}$ при необходимости приближения матрицей ранга ${\displaystyle r}$ меньшего чем ${\displaystyle n}$ часто используют компактное представление разложения^[3]:

${\displaystyle M=U_{r}\Sigma _{r}V_{r}^{*}.}$

Вычисляются только ${\displaystyle r}$ столбцов ${\displaystyle U}$ и ${\displaystyle r}$ строк ${\displaystyle V^{*}}$. Остальные столбцы ${\displaystyle U}$ и строки ${\displaystyle V^{*}}$ не вычисляются. Это экономит большое количество памяти при ${\displaystyle r\ll n}$.

Приведем пример, допустим ${\displaystyle m}$ это количество пользователей, каждый из которых проставил часть оценок фильмам, общее количество которых будем обозначать ${\displaystyle n}$, тогда матрица (сильно разреженная, т. к. каждый пользователь оценил лишь малую часть фильмов) будет обозначаться ${\displaystyle M}$ и иметь достаточно большую размерность ${\displaystyle [m\times n]}$.

При желании работать с матрицей меньшей размерности мы должны вычислить сингулярное разложение:

${\displaystyle M=U\Sigma V^{*}}$ при этом матрица ${\displaystyle \Sigma }$ как было сказано ранее является диагональной. После чего, если мы хотим сохранить только ${\displaystyle 90\%}$ информации, то мы должны взять ${\displaystyle r}$, таким образом, чтобы сумма квадратов первых элементов ${\displaystyle \Sigma }$ была ${\displaystyle 90\%}$ от общей суммы всех квадратов диагональных элементов ${\displaystyle \Sigma }$.

Таким образом мы получим ${\displaystyle U}$ размерностью ${\displaystyle [m\times r]}$ (взяв ${\displaystyle r}$ столбцов), ${\displaystyle \Sigma }$ с размерностью ${\displaystyle [r\times r]}$ и ${\displaystyle V^{*}}$ с ${\displaystyle [r\times n]}$. После, вместо матрицы ${\displaystyle M}$ мы можем манипулировать матрицей ${\displaystyle M'=U\Sigma }$ с меньшей размерностью ${\displaystyle [m\times r]}$, которую часто интерпретируют, как матрицу оценок пользователей по категориям фильмов.

Программные реализации

Численные алгоритмы нахождения сингулярного разложения встроены во многие математические пакеты. Например, в системах MATLAB и GNU Octave его можно найти командой

[U, S, V] = svd(M);

SVD входит в список основных методов многих математических библиотек, в том числе свободно распространяемых.
Так, например, существуют реализации

• В GNU Scientific library (GSL):

https://www.gnu.org/software/gsl/manual/html_node/Singular-Value-Decomposition.html

• Во framework'е ROOT, разрабатываемом в CERN и широко используемом в научной среде:

https://root.cern.ch/root/htmldoc/guides/users-guide/LinearAlgebra.html#svd

• В библиотеке Intel® Math Kernel Library (Intel® MKL).

https://software.intel.com/en-us/intel-mkl

• В библиотеке numpy для линейной алгебры в Python:

https://numpy.org/doc/stable/reference/generated/numpy.linalg.svd.html

• В библиотеке для машинного обучения tensorflow:

https://www.tensorflow.org/api_docs/python/tf/linalg/svd

• И некоторые другие

https://tedlab.mit.edu/~dr/SVDLIBC/
http://www.alglib.net/matrixops/general/svd.php

См. также

• Разложение матрицы
• Метод главных компонент
• Латентно-семантический анализ